Finding the Longest Common Subsequence (LCS) string

Difference between the length of the LCS and the LCS itself

The algorithm:

public static int solveLCS(String x, String y) { int i, j; /* =============================================== Initialize the base cases =============================================== for (j = 0; j < y.length()+1; j++) K[1][j] = 0; // x = "" ===> LCS = 0 for (i = 1; i < x.length()+1; i++) { /* ===================================================== Recycle phase: copy row K[1][...] to row K[0][...] ===================================================== */ for ( j = 0; j < y.length()+1; j++) K[0][j] = K[1][j]; K[1][0] = 0; for (j = 1; j < y.length()+1; j++) { if ( x.charAt(i-1) == y.charAt(j-1) ) { K[1][j] = K[0][j-1] + 1; } else { K[1][j] = max( K[0][j] , K[1][j-1] ); } } } // The value of LCS is in K[1][y.length()] return K[1][y.length()]; }

only computes the length of the LCS

Example:

x = ABCABCABC (x.length() = 8) y = BABACBAB (y.length() = 7) solveLCS(x,y) will compute: L[8][7] = 6

(i.e.., it can tell you that the LCS is 6 characters long)

Weakness of this algorithm:
(i.e., the algorithm does not tell you that the LCS is ABABAB.)
Herscheberg has developed a recursive algorithm to solve the LCS string that uses only O( m + n ) amount of computer memory.
The algorithm uses the LCS algorithm to perform the recursive step.
The algorithm description can be found in this research paper: click here (Algorithm "C" in the paper).

A divide and conquer algorithm to find the LCS string

Problem: find the LCS string of the following 2 strings:
A solution is:
(There are other LCS strings, e.g: ABABAB ( ABCABCABC and BABACBAB).
The algorithm that we study only find one solution, not all solution)

We can divide the find LCS string problem in to 2 smaller problems as follows:

Divide the first input string into 2 (approximately) equal halves:

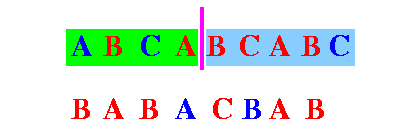
Note: (performance)

It is very important that we divide the first string in 2 equal length parts
Because this will ensure that the number of times we divide the string in half is: O(lg(n)) !

Now: If we split the second string in the correct place:
Then, the original LCS string problem can solved using the solutions of 2 smaller LCS string problems:
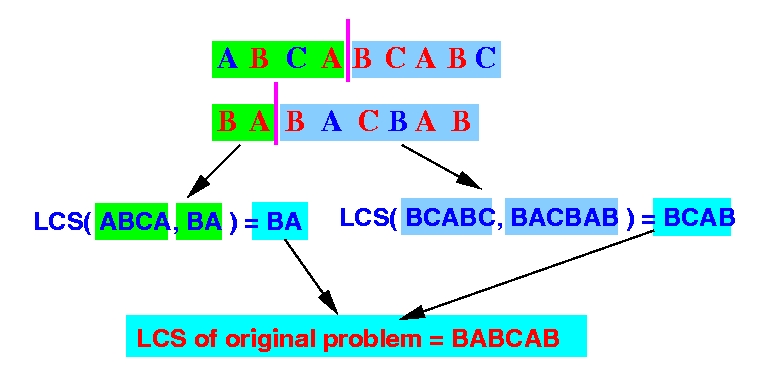
the Longest Common Substring pattern of the original problem:
is equal to the concatenation of the solutions of the following 2 smaller LCS problems:

Note 1: (on correctness)

After splitting the first string in half, you must find the correct split for second string
Warning:
Example: if we split the second string at the 3rd letter:
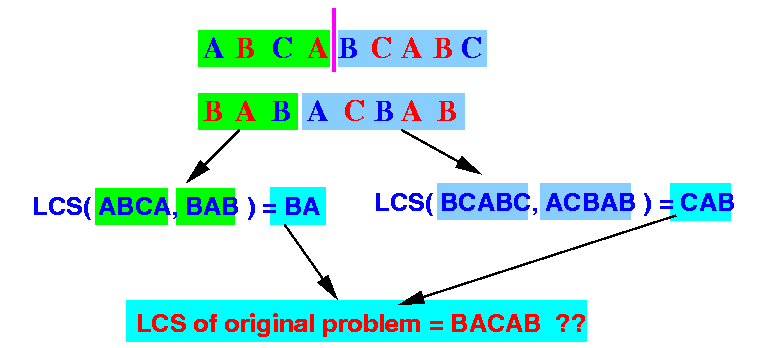
the concatenation of the 2 smaller LCS strings is not the LCS string of the original problem !!!!

Note 2: (repeat, in the case you may have missed the not on performance)

Summary/sketch of the divide and conquer algorithm for LCS string

The recursive algorithm to find a (one) Longest Common Subsequence string:

String findLCS_String( String x, String y ) { if ( base cases ) // We worry about base bases later !! { return (Base case solution); } else { Split string x in half: x1 = first half of x; x2 = second half of x; Find a correct split for string y: (we don't know how to do this yet) Let k = a correct split of string y; Split string y into: y1 = y[0..(k-1)]; y2 = y[k..n]; Solve smaller problems: Sol1 = findLCS_String( x1, y1 ); // LCS string of x1 and y1 Sol2 = findLCS_String( x2, y2 ); // LCS string of x2 and y2 Solve the original problem with Sol1 and Sol2: mySol = Sol1 + Sol2; return ( mySol ); } }

Notice that:

The recursive calls to findLCS_String() in the method are:

Sol1 = findLCS_String( x1, y1 ); // LCS string of x1 and y1 Sol2 = findLCS_String( x2, y2 ); // LCS string of x2 and y2

and the length of x1 and x2 is half the length of the original string x

That means that the depth of the recursion (= the number of recursive calls before you reach the base cases) for findLCS_String(x, y) is:

depth of findLCS_String(x, y) = lg( length(x) )

Example:

^ findLCS_Str("abcd", ...) length("abcd") = 4 | / \ | / \ depth=2 findLCS_Str("ab", ...) findLCS_Str("ab", ...) | / \ / \ | / \ / \ v findLCS_Str("a", .) findLCS_Str("b", .) findLCS_Str("c", .) findLCS_Str("d", .)

The depth of the recursion is lg(4) = 2

Finding a correct split for second string y

Condition that a correct split must satisfy:

We want to find the longest common subsequence:

If we split the problem into 2 smaller strings, in general, we will find a solution that is ≤ the longest common subsequence:

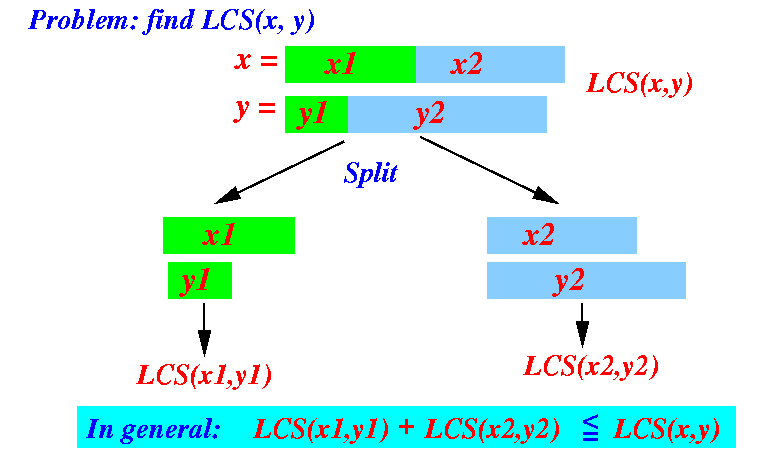
Example:

Find: LCS( "ABCDEF", AXCDYF" ) Answer: LCS( "ABCDEF", AXCDYF" ) = 4 (The LCS string is "ACDF")
A split may cause the LCS to become shorter because some characters cannot be matched up: "ABCDEF" "AXCDYF" / \ / \ "ABC" "DEF" "A" "XCDYF" LCS( "ABC", A" ) = 1 ("A") LCS( "DEF", "XCDYF" ) = 2 ("DF") because the "C" can't be matched

Condition that a correct split must satisfy:

Example of a correct split:
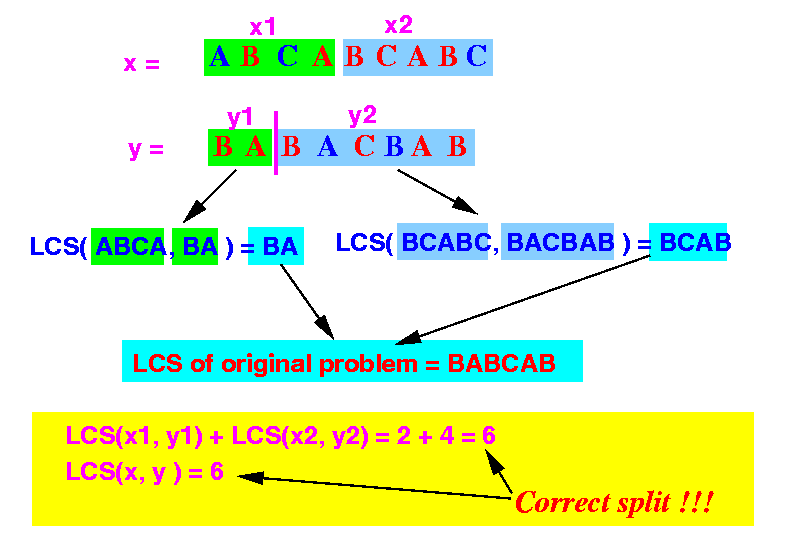
Example of an incorrect split:

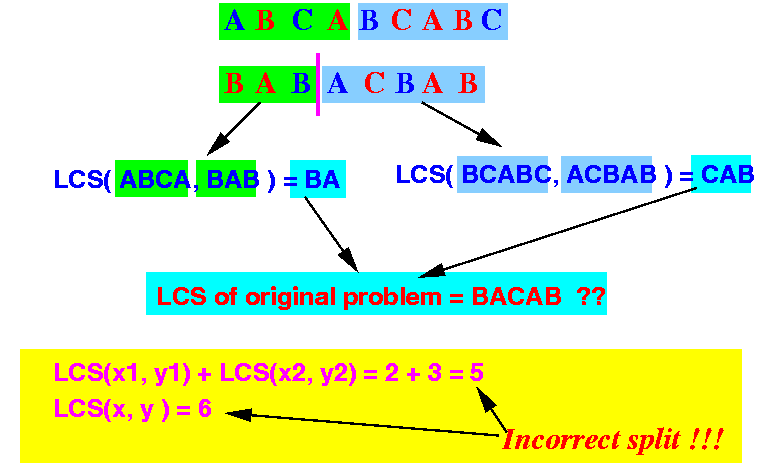
Conclusion:

We can use the (linear space) solveLCS() algorithm to find a correct split for second string y !!!!

Algorithm to find a correct split for string y: n = y.length(); for ( k = 0; k < n; k++ ) { y1 = y.substring(0, k); y2 = y.substring(k, n); if ( solveLCS(x1, y1) + solveLCS(x2,y2) == solveLCS(x,y) ) break; } How to split y: y1 = y.substring(0, k); y2 = y.substring(k, n);

Let's add this step to the algorithm (piece meal algorithm development)....

Refined (more detailed) algorithm to find a (one) Longest Common Subsequence string:

String findLCS_String( String x, String y ) { if ( base cases ) // We worry about base bases later !! { return (Base case solution); } else { Split string x in half: m = x.length(); mid = m/2; x1 = x.substring(0, mid); x2 = x.substring(mid, m); **************************************************************** Find a correct split for string y: n = y.length(); for ( k = 0; k < y.length(); k++ ) { y1 = y.substring(0, k); y2 = y.substring(k, n); if ( solveLCS(x1, y1) + solveLCS(x2,y2) == solveLCS(x,y) ) break; } **************************************************************** Split string y at the correct split: y1 = y.substring(0, k); y2 = y.substring(k, n); Solve smaller problems: Sol1 = findLCS_String( x1, y1 ); // LCS string of x1 and y1 Sol2 = findLCS_String( x2, y2 ); // LCS string of x2 and y2 Solve the original problem with Sol1 and Sol2: mySol = Sol1 + Sol2; return ( mySol ); } }

Base cases in the LCS string problem

Since we cut the first input string in half in each recursion, we must stop cutting when we have one of these 2 strings:

the empty string (if we started with an empty string)
a string with one single character

Example:

"abcde" / \ "ab" "cde" / \ / \ "a" "b" "cd" "e" / \ "c" "d"

Base cases in the LCS string problem:

Case 1: the empty string
Solution:

Case 2: the "?" (single character string)

Solution:

If "?" is a character in y, then:
Otherwise:

Example:

LCS_String( "c", "abracadabra" ) = "c" LCS_String( "x", "abracadabra" ) = ""

The complete findLCS_String(x,y) algorithm in pseudo code:

String findLCS_String( String x, String y ) { if ( x.length() == 0 ) // Base case "" { return (""); // LCS = "" ******* } else if ( x.length() == 1 ) // Base case "?" { /* ================================= Find that character in y ================================= */ for ( int j = 0; j < y.length(); j++ ) if ( y.charAt(j) == x.charAt(0) ) return( x ); // Found: LCS = x **** return (""); // Not found: LCS = "" **** } else // Divide and conquer { Split string x in half: m = x.length(); mid = m/2; x1 = x.substring(0, mid); x2 = x.substring(mid, m); Find a correct split for string y: n = y.length(); for ( k = 0; k < y.length(); k++ ) { y1 = y.substring(0, k); y2 = y.substring(k, n); if ( solveLCS(x1, y1) + solveLCS(x2,y2) == solveLCS(x,y) ) break; } Split string y at the correct split: n = y.length(); y1 = y.substring(0, k); y2 = y.substring(k, n); Solve smaller problems: Sol1 = findLCS_String( x1, y1 ); // LCS string of x1 and y1 Sol2 = findLCS_String( x2, y2 ); // LCS string of x2 and y2 Solve the original problem with Sol1 and Sol2: mySol = Sol1 + Sol2; return ( mySol ); } }

Herschberg's Algorithm for finding the LCS string

Herschberg's Algorithm in Java:

public static String findLCS_String(String x, String y) { int mid, i, j; int m, n; String C = ""; m = x.length(); // m = length of x n = y.length(); // n = length of y /* ===================================================== Base case 1: "" ===================================================== */ if ( m == 0 ) { return ""; // LCS = "" } /* ===================================================== Base case 2: x = "?" ===================================================== */ if ( m == 1 ) { /* ===================================== The input x consists of 1 character Find the single common character in y ===================================== */ for ( i = 0; i < n; i++ ) if ( y.charAt(i) == x.charAt(0) ) return( x ); // Found: LCS = x return ""; // Not found: LCS = "" } /* ===================================================== General case: x has 2 or more characters ===================================================== */ String x1="", x2=""; // x1 = first half of x, x2 = second half int c1=0, c2=0; // c1 = length of first LCS, c2 = second int c = solveLCS( x, y ) ; // This is the sum of the correct split x1 = x.substring( 0, m/2 ); // First half of x x2 = x.substring( m/2, m ); // Second half of x /* -------------------------------------------------- Find a correct split of y -------------------------------------------------- */ for ( k = 0; k < n; k++ ) { c1 = solveLCS( x1, y.substring(0, k) ) ; // LCS of first half c2 = solveLCS( x2, y.substring(k, n) ) ; // LCS of second half if ( c1 + c2 == c ) break; // Found a correct split of y !!! } /* -------------------------------------------------- Here: k = a correct split location of y .... Solve smaller problems -------------------------------------------------- */ String y1 = y.substring( 0, k ); String y2 = y.substring( k, n ); String sol1 = findLCS_String( x1, y1 ); String sol2 = findLCS_String( x2, y2 ); /* ------------------------------------------------------------ Use solution of smaller problems to solve original problem ------------------------------------------------------------ */ return ( sol1 + sol2 ); }

Example Program: (Demo above code)

Prog file: click here

How to run the program:

Right click on link(s) and save in a scratch directory
To compile: javac Hirschberg.java
To run: java Hirschberg

Sample output:

x = abcabcabc y = babacbab LCS_String(abcabcabc,babacbab) LCS_String(abca,ba) LCS_String(ab,b) LCS_String(a,) LCS_String(b,b) LCS_String(ca,a) LCS_String(c,) LCS_String(a,a) LCS_String(bcabc,bacbab) LCS_String(bc,bac) LCS_String(b,b) LCS_String(c,ac) LCS_String(abc,bab) LCS_String(a,ba) LCS_String(bc,b) LCS_String(b,b) LCS_String(c,) LCS = babcab
Note: Length("abcabcabc") = 9 Depth of rcursion = 4 (lg(9) = 3.17))