- The 0-1 knapsack problem:
- Given N types of items:
- The item type i has
a weight wi
- The item type i has a value vi
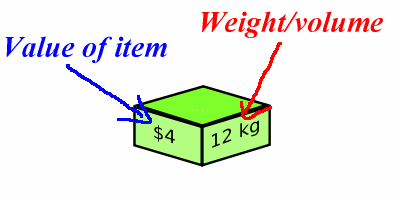
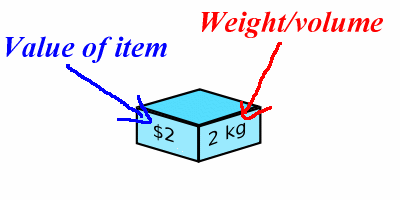
... 0,1 refers to:
- There is exactly one
item
of
each type of item available
(I.e.: you can pack an item (you will then one of that item) or you can do not pack that item (you will then zero of that item)
- The item type i has
a weight wi
- Given a knapsack with
capacity W:

- Problem:
- Pack as many items into
the knapsack
such that the
total value of the
items packed is
maximized
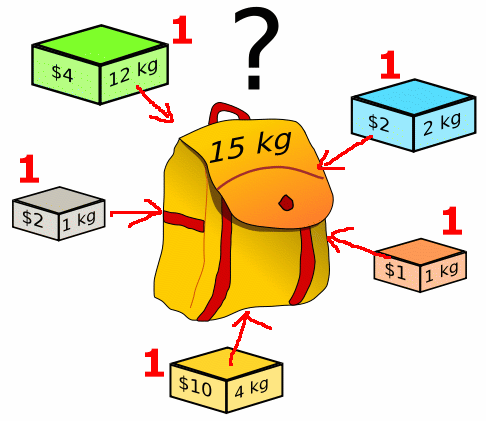
Note: you cannot exceed the capacity of the knapsack !
- Pack as many items into
the knapsack
such that the
total value of the
items packed is
maximized
- Given N types of items:
- Define:
- x1 = # items of type 1 packed into the knapsack
- x2 = # items of type 2 packed into the knapsack
- ...
- xN = # items of type N packed into the knapsack
- Then:
- Total weight of item packed =
w1 × x1 +
w2 × x2 + ...
+ wN × xN
- wi = weight of an item i
- Total value of item packed =
v1 × x1 +
v2 × x2 + ...
+ vN × xN
- vi = value of an item i
- Total weight of item packed =
w1 × x1 +
w2 × x2 + ...
+ wN × xN
- Note:
- We will
not
solve
the 0,1 knapsack problem as
a constrained optimilization problem
here....
We will do this later in the constrained optimalization section
- We will
not
solve
the 0,1 knapsack problem as
a constrained optimilization problem
here....
- Items:
- w1 = 2 and v1 = 3
- w2 = 4 and v2 = 5
- w3 = 5 and v3 = 6
- w4 = 7 and v4 = 8
- w5 = 9 and v5 = 10
- Question:
- Pack a knapsack with capacity = 20 so that the total value is maximized
Solution:
- w1 = 2 and v1 = 3
- w2 = 4 and v2 = 5
- w3 = 5 and v3 = 6
- w5 = 9 and
v5 = 10
- Total value = 24, Total weight = 20
- Question:
- Pack a knapsack with capacity = 19 so that the total value is maximized
Solution:
- w1 = 2 and v1 = 3
- w2 = 4 and v2 = 5
- w3 = 5 and v3 = 6
- w4 = 7 and
v4 = 8
- Total value = 22, Total weight = 18
- How to solve
a 0,1 knapsack problem
using the
solution of a
smaller
0,1 knapsack problem:
- My problem:
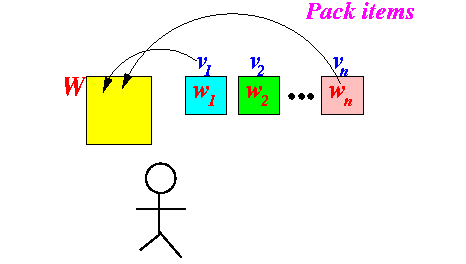
How can I pack the items in the knapsack so that the value is maximized (without exceeding the capacity constraint)
- Fact: I have the following
choice on
item n
- I can leave item n
out of the knapsack
- I can pack item n in the knapsack
- I can leave item n
out of the knapsack
- Let me hire
some people to solve the following
2 (smaller) problems:
- Pack a knapsack of capacity
W with
only items
1, 2, 3, ..., n−1
so that the value is
maximized
(i.e., I am leaving item n out
of the knapsack)
- Pack a knapsack of capacity W − wn with only items 1, 2, 3, ..., n−1 so that the value is maximized (i.e., I have packed item n in the knapsack)
Graphically:
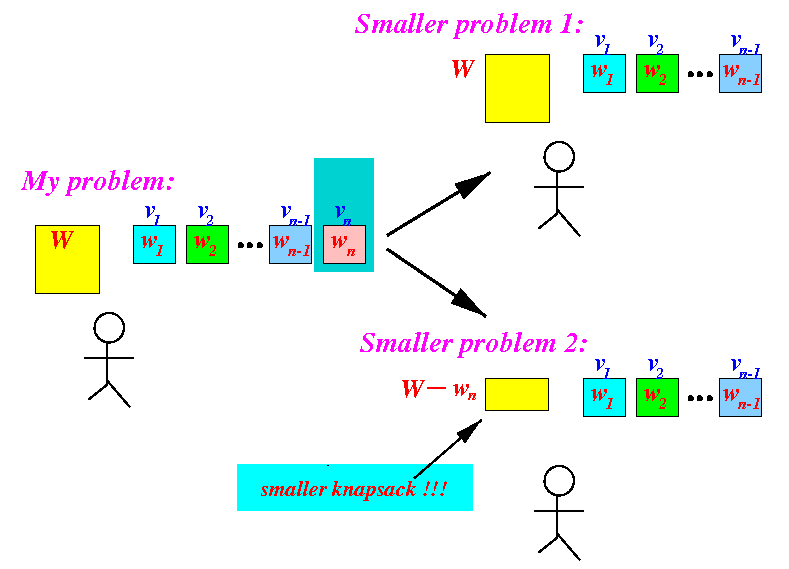
Notice that:
- Item n is
not inside
the smaller knapsack !!!
- In recursion,
the problem must
remain the same !!!
(E.g., you can't have a "half packed" knapsack - you must start with an empty knapsack)
You can only can the size of the problem !!!
- Pack a knapsack of capacity
W with
only items
1, 2, 3, ..., n−1
so that the value is
maximized
(i.e., I am leaving item n out
of the knapsack)
- Suppose the helpers
return these
solutions to me:
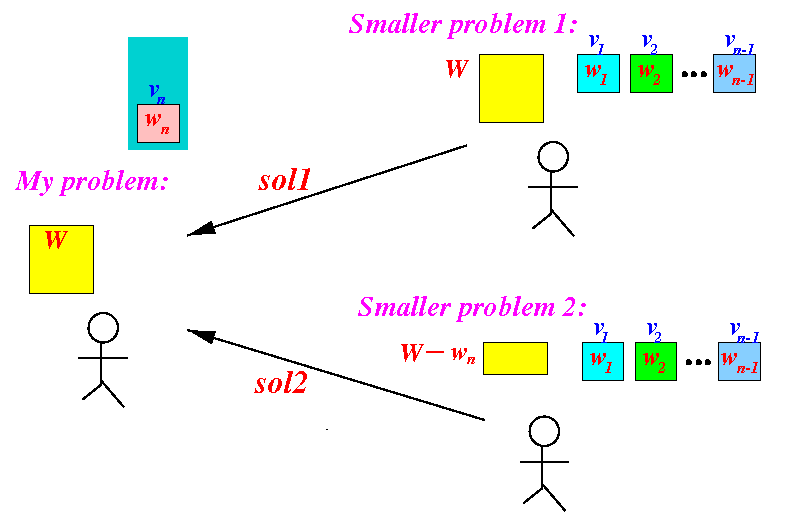
- Then I can solve
my problem as follows:
- If I leave out
item n,
the maximum value is:
- sol1 (returned by the helper)
- If I pack
item n,
the maximum value is:
- sol2
+ vn
(I must add the value of item n to sol2 to obtain my solution because helper 2 did not know that item n was packed --- I gave him a smaller knapsack --- leaving space for item n that I will put in later !!!)
- sol2
+ vn
- If I leave out
item n,
the maximum value is:
- The overall
maximum value is:
- max( sol1, sol2 + vn )
- My problem:
- Concrete example:
- Pack these items into the
knapsack:
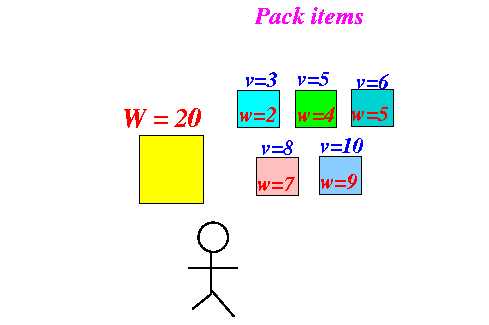
- Let someone else solve
these 2 smaller problems:
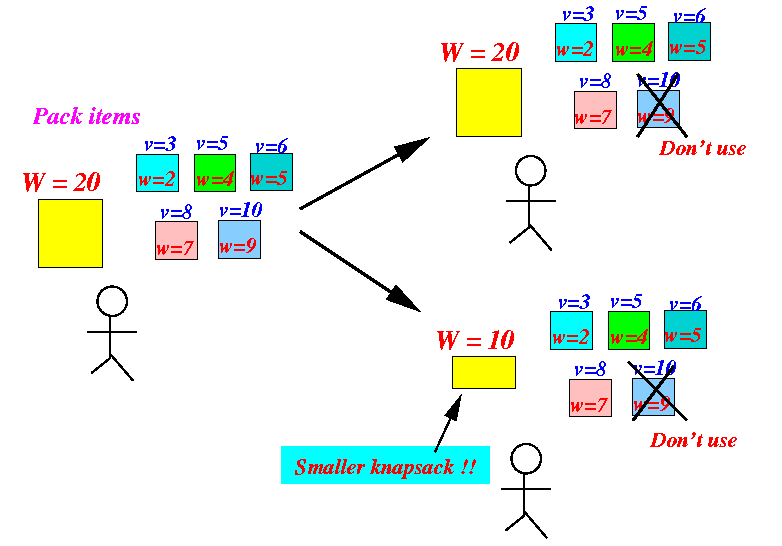
- I will get back
the following solutions:
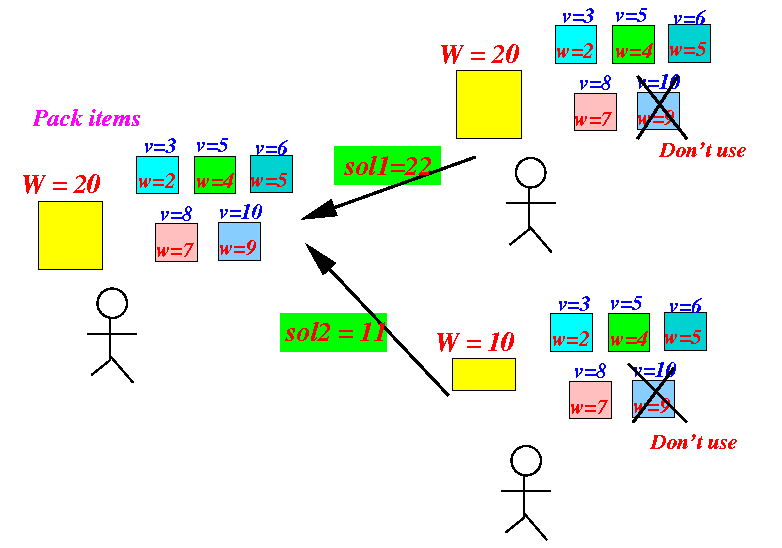
Therefore:
- If I
do not pack
the item with w = 9,
my maximum value =
22
- If I do pack the item with w = 9, my maximum value = 11 + 10 = 21
Therefore:
- maximum value = 22
- If I
do not pack
the item with w = 9,
my maximum value =
22
- Pack these items into the
knapsack:
- Caveat:
- We can only pack
item n
into the knapsack
if:
- Capacity of the knapsack ≥ wn !!!
- We can only pack
item n
into the knapsack
if:
- Define:
- M(k, C) =
solution for the 0,1 knapsack problem
packing k items
in a knapsack of capacity C
M(k, C) = the maximum value of v1×x1 + v2×x2 + ... + vk×xk
subject to: w1×x1 + w2×x2 + ... + wk×xk ≤ C
wi = 0 or 1, for i = 1, 2, ..., k
- M(k, C) =
solution for the 0,1 knapsack problem
packing k items
in a knapsack of capacity C
- Pseudo code:
int M( k, C ) { // Let us not worry about the base bases for now.... /* ========================================== Divide and conquer procedure ========================================== */ if ( wk > C ) { /* -------------------------------- Item k does not fit !!! -------------------------------- */ myFinalSol = M( k-1, C ); // You have to leave item k out !!! } else { sol1 = M( k-1, C ); // Smaller problem when we leave out item k sol2 = M( k-1, C-wk ); // Smaller problem when we pack item k mySol1 = sol1; // I did not pack item k, no additional value mySol2 = sol2 + vk; // I PACKED item k !!! myFinalSol = min ( mySol1, mySol2 ); } return ( myFinalSol ); }
- Base cases:
- M(k, C) =
solution for the 0,1 knapsack problem
packing
k items
in a knapsack of capacity C
- Facts:
- If you have no items,
you can't pack any item
into the knapsack
Therefore:
- M(0, C) = 0, for any capacity of knapsacks !
- If the knapsack is full
(i.e., zero capacity),
you can't pack any item
into the knapsack
Therefore:
- M(k, 0) = 0, for any k items !
- If you have no items,
you can't pack any item
into the knapsack
Summary:
M(k, 0) = 0; for all k (can't packet anything into a 0-capacity knapsack) M(0, C) = 0; for all C (can't packet anything if you have no items left !) - M(k, C) =
solution for the 0,1 knapsack problem
packing
k items
in a knapsack of capacity C
- Psuedo code
/* =========================================================== M(k, C) = max. achievable value packet into a knapsack of capacity C using items 1, 2, ..., k =========================================================== */ int M(int k, int C) { /* ============================== Base cases ============================== */ if ( k == 0 ) { return(0); // no items left } if ( C == 0 ) { return(0); // 0 capacity } /* ========================================== Divide and conquer procedure ========================================== */ if ( wk > C ) { /* -------------------------------- Item k does not fit !!! -------------------------------- */ myFinalSol = M( k-1, C ); // You have to leave item k out !!! } else { sol1 = M( k-1, C ); // Smaller problem when we leave out item k sol2 = M( k-1, C-wk ); // Smaller problem when we pack item k mySol1 = sol1; // I did not pack item k, no additional value mySol2 = sol2 + vk; // I PACKED item k !!! myFinalSol = min ( mySol1, mySol2 ); } return ( myFinalSol ); }
- Java code:
static int M(int[] v, int[] w, int k, int C) { int sol1, sol2, mySol1, mySol2, myFinalSol; /* --------------------------- Base cases --------------------------- */ if ( k == 0 ) { return(0); // No more items to pick from } if ( C == 0 ) { return(0); // No more space } /* -------------------------------------------- Check if we can use the n-th typed item -------------------------------------------- */ if ( w[k-1] > C ) // Item k-1 does not fit... { myFinalSol = M(v, w, k-1, C); // We must leave item k-1 out } else { /* ==================================== Solve smaller problems ==================================== */ sol1 = M(v, w, k-1, C); // Try leaving item k out sol2 = M(v, w, k-1, C - w[k-1]); // Try packing item k /* ========================================================== Use solution of smaller problems to solve my problem ========================================================== */ mySol1 = sol1; // I did not pack item k-1, so no added value mySol2 = sol2 + v[k-1]; // I packed item k-1, so add v[k-1] ! if ( mySol1 > mySol2 ) myFinalSol = mySol1; else myFinalSol = mySol2; } return(myFinalSol); // Return my solution }
- Example Program:
(Demo above code)

- Prog file: click here
How to run the program:
- Right click on link(s) and
save in a scratch directory
- To compile: javac Knapsack_01.java
- To run: java Knapsack_01
- Data structure:
- The function:
static int M(int[] v, int[] w, int k, int j)uses parameters k and C that take on these values:
k = 0, 1, 2, ....., n // n = # items C = 0, 1, 2, ....., W // W = capacity of the knapsack
Each solution must be stored
- Data structure:
need to use a 2 dim. array
int[][] M = new int[n+1][W+1];
- The function:
- Base cases:
- The code for the
base cases:
stored in M(k,C) ===========> M[k][C] if ( k == 0 ) { return(0); // No more items to pick from } if ( C == 0 ) { return(0); // No more space }
- This result is the following values stored in the
data structure:
/* --------------------------- Base cases --------------------------- */ for ( j = 0; j <= W; j++ ) M[0][j] = 0; // (k=0) No more items to pick from for ( i = 0; i <= n; i++ ) M[i][0] = 0; // (C=0) No more space
- The code for the
base cases:
- The recursive case:
- The code for the
recursive case is:
M( k, C ): (answer is myFinalSol which will be stored in M[k][C]) ==================== if ( w[k-1] > C ) // Item k-1 does not fit... { myFinalSol = M(v, w, k-1, C); // We must leave item k-1 out } else { /* ==================================== Solve smaller problems ==================================== */ sol1 = M(v, w, k-1, C); // Try leaving item k out sol2 = M(v, w, k-1, C - w[k-1]); // Try packing item k /* ========================================================== Use solution of smaller problems to solve my problem ========================================================== */ mySol1 = sol1; // I did not pack item k-1, so no added value mySol2 = sol2 + v[k-1]; // I packed item k-1, so add v[k-1] ! if ( mySol1 > mySol2 ) myFinalSol = mySol1; else myFinalSol = mySol2; } return(myFinalSol); // Return my solutionwhich result in the following iterative code:
if ( w[k-1] > C ) // Item k-1 does not fit... { M[k][C] = M[k-1][C]; // We must leave item k-1 out } else { /* ==================================== Solve smaller problems ==================================== */ sol1 = M[k-1][C]; // Try leaving item k out sol2 = M[k-1][C - w[k-1]]; // Try packing item k /* ========================================================== Use solution of smaller problems to solve my problem ========================================================== */ mySol1 = sol1; // I did not pack item k-1, so no added value mySol2 = sol2 + v[k-1]; // I packed item k-1, so add v[k-1] ! if ( mySol1 > mySol2 ) M[k][C] = mySol1; else M[k][C] = mySol2; }
- Note:
make sure you iterate
with the
data flow:
for ( k = 1; k <= n; k++ ) for ( C = 1; C <= W; C++ ) compute M[k][C] ....
- The code for the
recursive case is:
- Java code:
/* =========================================================== M(n, W) = max value achieved by knapsack with capacity W filled with items 0, 1, ..., n-1 =========================================================== */ static int M(int[] v, int[] w, int n, int W) { int sol1, sol2, mySol1, mySol2; int k, C; int[][] M; M = new int[n+1][W+1]; // Data structure /* --------------------------- Base cases --------------------------- */ for ( int j = 0; j <= W; j++ ) M[0][j] = 0; // (k=0) No more items to pick from for ( int i = 0; i <= n; i++ ) M[i][0] = 0; // (C=0) No more space /* ==================================== Compute M[k][C]: ==================================== */ for ( k = 1; k <= n; k++ ) { for ( C = 1; C <= W; C++ ) { /* -------------------------------------------- Check if we can use the n-th typed item -------------------------------------------- */ if ( w[k-1] > C ) // Item k-1 does not fit... { M[k][C] = M[k-1][C]; // We must leave item k-1 out } else { /* ==================================== Solve smaller problems ==================================== */ sol1 = M[k-1][C]; // Try leaving item k out sol2 = M[k-1][C-w[k-1]]; // Try packing item k /* ========================================================== Use solution of smaller problems to solve my problem ========================================================== */ mySol1 = sol1; // I did not pack item k-1, so no added value mySol2 = sol2 + v[k-1]; // I packed item k-1, so add v[k-1] ! if ( mySol1 > mySol2 ) M[k][C] = mySol1; else M[k][C] = mySol2; } } } return(M[n][W]); // Max value to pack n item in knapsack cap W }
- Example Program:
(Demo above code)

- Prog file: click here
How to run the program:
- Right click on link(s) and
save in a scratch directory
- To compile: javac Knapsack1_dp.java
- To run: java Knapsack1_dp
- O(n × W)
(just look at the nested for-loop....)
-
n = # items
W = capacity of knapsack