- Worst case:
- get(Key k):
- O(n) (n = # keys)
(Happens when all keys are in a single cluster)
- O(n) (n = # keys)
- put(Key k, Value v):
- O(n) (n = # keys)
(Happens when the new key k lands in the single cluster)
- O(n) (n = # keys)
- remove(Key k) :
- O(n) (n = # keys)
(Happens when the key k is in the single cluster)
- O(n) (n = # keys)
- get(Key k):
- Example 1:
- Half of the time, you get
paid $10
Half of the (other) time, you get paid $20
- On the average, you make 0.5 × $10 + 0.5 × $20 = $15 (per day)
- Half of the time, you get
paid $10
- Example 2:
- Monday,
you get paid $10
Tuesday, you get paid $10
Wednesday, you get paid $30
Thursday, you get paid $30
Friday, you get paid $20Average pay per day = (10 + 10 + 30 + 30 + 20)/5 = 20
- Different way to compute the average:
- 2/5 of the time, you get paid $10
- 2/5 of the time, you get paid $30
- 1/5 of the time, you get paid $20
- Average pay = (2/5) × 10 + (2/5) × 30 + (1/5) × 20 = 20 (per day)
- Monday,
you get paid $10
- Mathematical expectation (average):
- An operation has
many different outcomes:
1, 2, 3, 4, ....
For each outcome, a different cost is incurred
- Outcomes and costs:
- Outcome k
occurs with
frequency
fk
- Outcome k incurs a cost of Ck
- Outcome k
occurs with
frequency
fk
- The average cost incurred
by the operation is then:
Avg. cost = f1×C1 + f2×C2 + ....
- An operation has
many different outcomes:
1, 2, 3, 4, ....
- The average cost of an
operation in a
Hash Map data structure
depends on:
- The occupancy level (or load factor) of the hash table
The higher the load factor, the more likely we would need to search for an entry or an empty slot (for insertion)
- Definition: Load factor (a)
# entries n Load factor a = ------------ = --- array size N
- Probability that an (array) slot
is occupied:
# occupied entries Ҏ[ an array slot is occupied by an entry] = -------------------------- Total # entries in array n = --- NConclusion:
- The load factor a is equal to the probability that a slot in the array is occupied
Important fact from Theory of Probability:
- Probability[ some event ] ~= (approximately equal) the frequency of that event !!!
Example:
- Roll a dice for
6,000,000 times
Approximately 1,000,000 of the rolls will come up 6
- Therefore:
- frequence(6) ~= 1/6
(And of course: probability(roll = 6) = 1/6)
- Insert operation:
- Find an empty slot
(For simplicity, we assume no AVAILABLE entries)
- Insert new entry in
the empty slot
- Note:
- If the key was found before we encounter an empty slot, the performance will be better than what we are computing :-)
- Find an empty slot
- Information
needed
to compute the average performance
of the insert operation:
- How often (frequent) do we need to
probe 1 slot
to find an empty slot
How many operations (running time) do we need in this case - How often (frequent) do we need to
probe 2 slot
to find an empty slot
How many operations (running time) do we need in this case - How often (frequent) do we need to
probe 3 slot
to find an empty slot
How many operations (running time) do we need in this case - And so on...
- How often (frequent) do we need to
probe 1 slot
to find an empty slot
- Frequency of
probing k array elements
in a search operation
using linear probing:
- Fact:
- Probing ends when we encounters an empty slot
- Starting at the hash index location:
(probing the first slot)
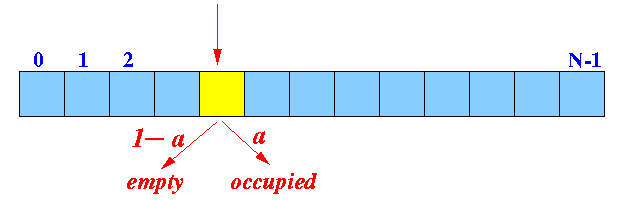
-
Ҏ[ yellow slot empty ] = 1 − a
Ҏ[ yellow slot occupied ] = aTherefore:
- Probability[ probe 1 slot ] = 1 − a
- If slot was occupied, we continue the probe:
(probing the second slot)
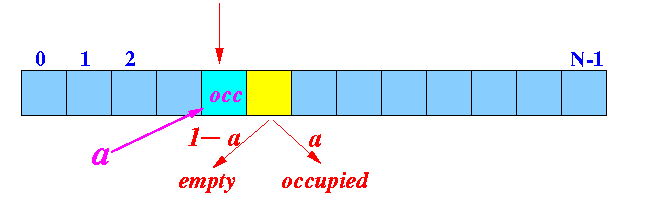
-
Ҏ[ yellow slot empty ] = a × (1 − a)
Ҏ[ yellow slot occupied ] = a × aTherefore:
- Probability[ probe 2 slots ] = a × (1 − a)
- If the second slot was occupied, we
continue the probe:
(probing the 3rd slot)
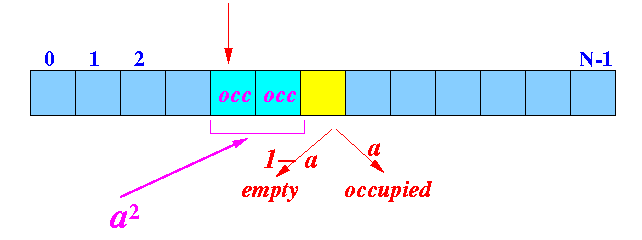
-
Ҏ[ yellow slot empty ] = a2
× (1 − a)
Ҏ[ yellow slot occupied ] = a2 × aTherefore:
- Probability[ probe 3 slots ] = a2 × (1 − a)
- And so on:
- Probability[ probe 4 slots ] = a3 × (1 − a)
- Probability[ probe 5 slots ] = a4 × (1 − a)
- ....
- Fact:
- Summary: number of probes (= operations) used
and their probabilities
(= frequencies):
- # probes = 1
(i.e., hash slot is empty)
frequency = (1 - a)
- # probes = 2
(i.e., hash slot is
occupied and the
next slot is empty)
frequency = a×(1 - a)
- # probes = 3
(i.e., hash slot is
occupied, the
next slot is occupied)
and the
3rd slot is empty)
frequency = a2×(1 - a)
- And so on...
- # probes = 1
(i.e., hash slot is empty)
- Average number of probes to find an
empty slot:
Avg. # probes = (1 - a) × 1 + a(1 - a) × 2 + a2(1 - a) × 3 + ... = (1 - a) × ( 1 + a×2 + a2×3 + ... ) = (1 - a) × ( 1×a0 + 2×a1 + 3×a2 + 4×a3 + ... )
- Computing the inner sum
with
numerical algebra system Mathematica:
>> math In[0]:= Sum[ (k+1)*a^k, {k,0,Infinity} ] -2 -2 Out[0]= (-1 + a) = (1 - a)
- Therefore:
1 Avg. # slots probed (to find empty slot) = (1 - a) * ------- (1 - a)2 1 = ------- (1 - a)Graphically:
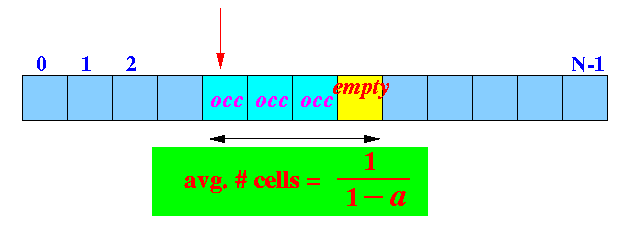
- Example:
- The map uses an array of
10000 elements
- Currently, there are 1000 entries in
the map
- Then an put(k, v) operation will
search on the
average this many entries:
a = 1000/10000 = 0.1 (1-a) = 0.9 1 1 Avg. # probes = ----- = ----- = 1.11111 1-a 0.9
- The running time of
the put(k,v) operation is then:
Running time put(k,v) = 1.11111 operations
- The map uses an array of
10000 elements
- The running time of
remove(k) is the
same as that of
get(k)
because:
- In remove(k), we
must first
find the entry using the
key k
- Once the entry (with key k) has
been found,
removing the
entry takes
O(1) time
(Set the value to the special AVAILABLE value)
- In remove(k), we
must first
find the entry using the
key k
- Locating an entry:
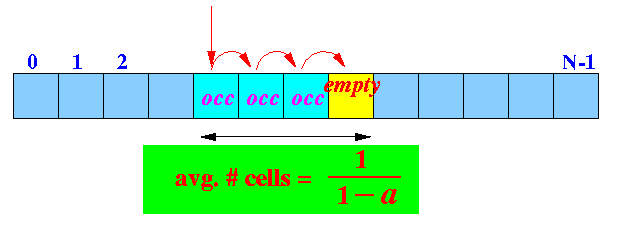
Note:
- The search operation
will end when it finds and
empty cell
- Therefore:
1 Avg. # cells searched ≤ ------- 1 - a
- The search operation
will end when it finds and
empty cell
- The insert, lookup and delete operation
in a hash table using
open addressing
is:
O( 1/(1 - a) ) ~= O(1) as long as a is small, (say < 0.5)