- The maximal matching problem in
a bi-partite graph can be transformed into a
maximum network flow problem.
- Add a
source S and
a sink T
- Connect source S to
every node of the
first set
- Connect every node of the second set to the sink T
- Assign the capacity 1 to every edge in the network
- Add a
source S and
a sink T
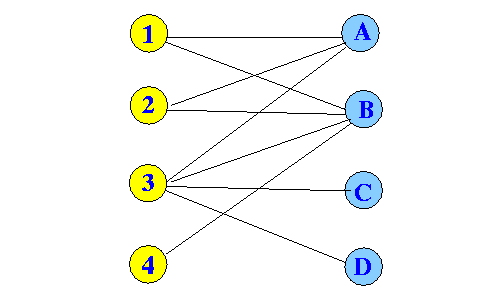
- Example:
Corresponding max flow problem:
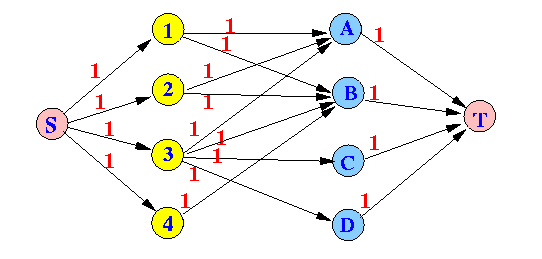
- Therefore:
- We could use the flow augnmenting path algorithm to solve the maximum matching problem in the bi-partite graph
But... there is a much easier algorithm :-)
- Definition:
alternating path with respect to
a given matching M
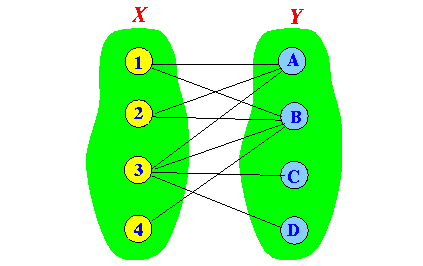
- Let G = (X, Y, E)
be a bi-partite graph where the vertices are
divided into the sets
X and
Y and
E = the edges.
Example:
- Let M = a
matching in the graph G
Example: (the red edges represent the matching M)
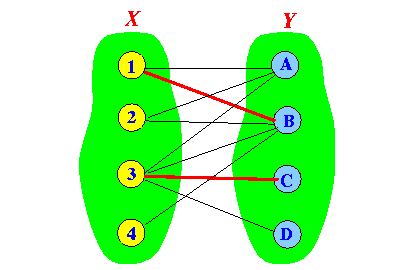
- An alternating path P
with respect to
a matching M is a
path that satisfies the
following conditions:
- P starts in a vertex ∈ X
- P
ends
in a vertex ∈ Y
- The odd-numbered edges in path P are ∉ M (i.e., not an edge in the matching)
- The even-numbered edges
in
path P
are ∈ M
- P must end in a vertex that is not matched up with any vertex in X
- Let G = (X, Y, E)
be a bi-partite graph where the vertices are
divided into the sets
X and
Y and
E = the edges.
- Examples:
Alternating path 1 Alternating path 2 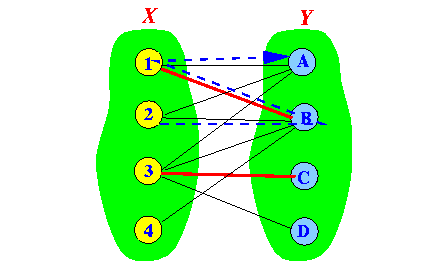
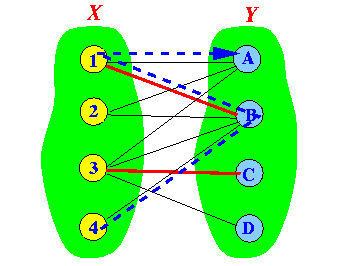
Note:
- An alternating path will
starts
in a vertex ∈ X
and ends
in a vertex ∈ Y
- An alternating path
must have
an
odd-number
of edges !!!
- An alternating path will
visit nodes in X and Y
alternatedly
(this is due to the nature of a
bi-partite graph)
- Just remember:
- To go forward,
use an edge that is
not part of the matching
- To go backward, use an edge that is part of the matching
- To go forward,
use an edge that is
not part of the matching
- An alternating path will
starts
in a vertex ∈ X
and ends
in a vertex ∈ Y
- Fact:
- When there is an alternating path with respect to a matching, the matching is not optimal
How to increase the matching:
- The size of the matching can
be increased by
inverting the
edges of the
alternating path
- I.e.: "flip" the edges in the alternating path
- Example 1:
Alternating path Improved matching 
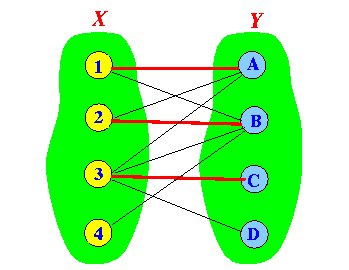
- Example 2:
Alternating path Improved matching 
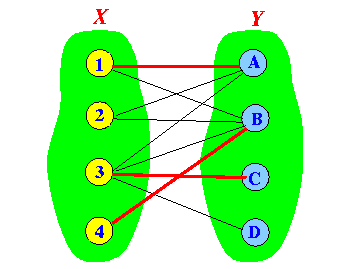
- Algorithm to find
an alternating path:
Given: Bi-partite graph (X,Y) A matching M in (X,Y) for ( each x ∈ X and x is not matched ) { label x by *; // x is current candidate repeat { 1. Apply the odd-edge label algorithm: for ( each y ∈ Y and y is not labeled ) if ( some adjacent node xk of y has a label ) label y with xk; 2. Apply the even-edge label algorithm: for ( each x ∈ X and x is not labeled ) if ( some adjacent node yk of x has a label ) label x with yk; } until no more nodes can be labeled /* ====================================== "Breakthrough" test ====================================== */ if ( a node yk ∈ Y is labeled and y ∉ M ) { there is an alternating path from x to yk } else { try next node x (if there are more candidates left) } }
- Example:
find an alternating path
with respect to the following
matching:
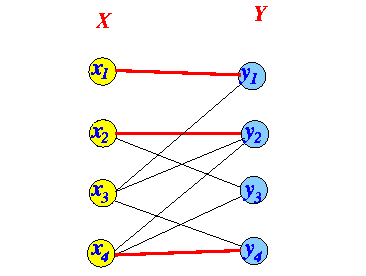
Note:
- Initially, all nodes do not have any label
- Execution of the
algorithm:
(with additional comments
for clarification)
- Label the
first vertex xi
∈ X
that is not in the matching
with the
label
*:
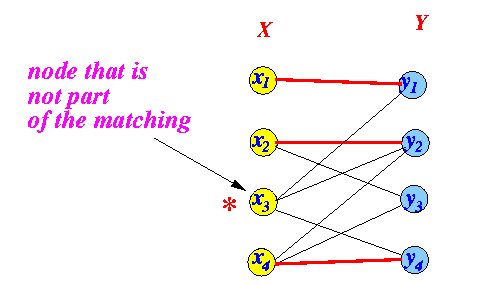
Note:
- The labeling procedure will
find an alternating path
that ends in
the node labeled by
*
- You must apply the labeling procedure to other unlabeled nodes ∈ X if you fail to an alternating path for the first node.
There are 2 label procedures that you apply in alternating order:
- A odd-edge
label procedure
- Use this procedure to label node ∈ Y
- A even-edge
label procedure
- Use this procedure to label node ∈ X
- The labeling procedure will
find an alternating path
that ends in
the node labeled by
*
- Odd-edge labeling
procedure:
- Label all unlabeled nodes ∈ Y that are incident to an edge ∉ matching with the ID of the neighbor node if that node has a label:
Example:
- Before:
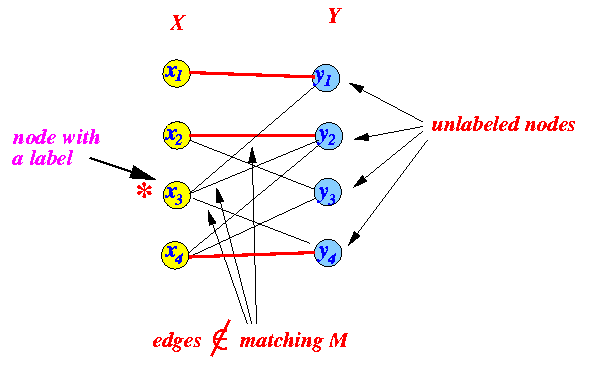
-
Label the unlabeled nodes
in Y with
node id
x3:
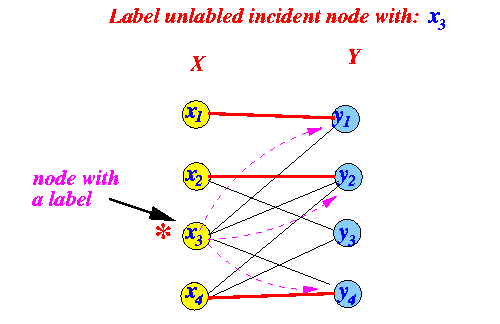
- Result:
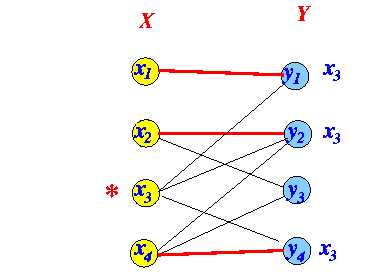
- Even-edge labeling
procedure:
- Label all unlabeled nodes ∈ X that are incident to an edge ∈ matching with the ID of the neighbor node if that node has a label
Example:
- Before the labeling took place:
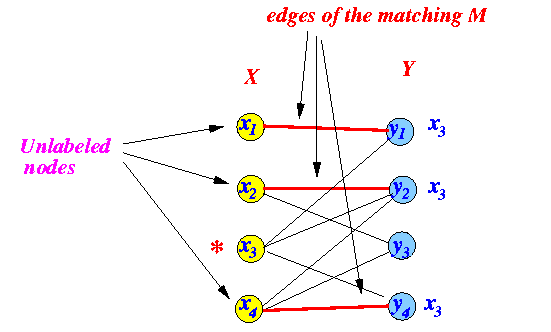
-
Label all
unlabeled nodes ∈ X
that are
incident to
an labeled node in
Y:
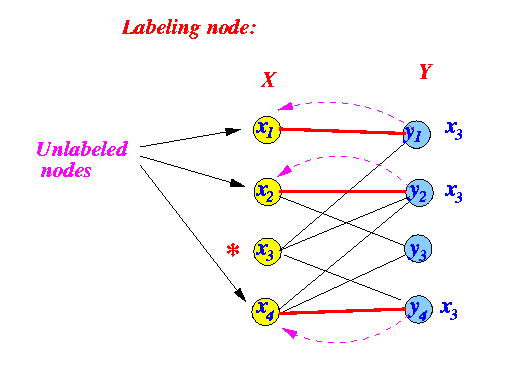
- Result:
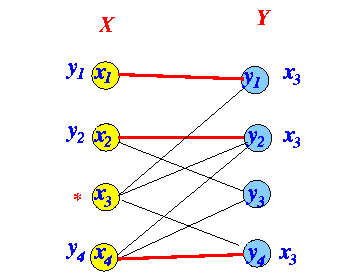
- Repeat the
(odd-edge labeling and
even-edge labeling)
procedure
until
no more nodes
can be labeled
- Apply the odd-edge labeling
procedure:
- Before:
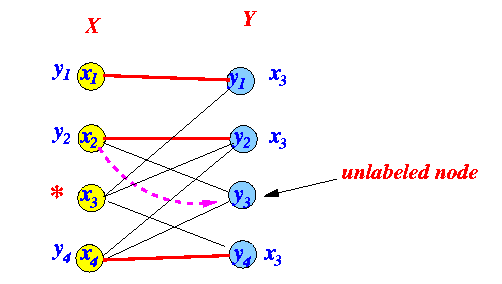
- Label the
unlabeled node with
the incident node id:
The odd-edge labeling cannot find any unlabeled node ∈ Y
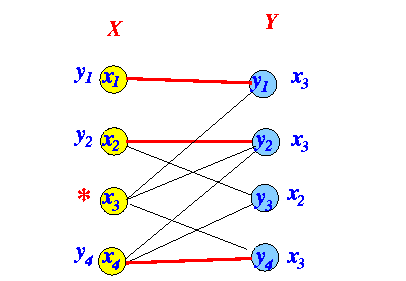
- Before:
Note:
- All nodes
are now labeled
Therefore:
- No more nodes can be labeled....
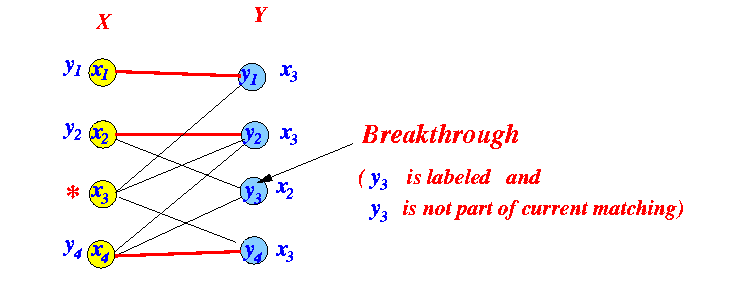
- Apply the odd-edge labeling
procedure:
- After the
labeling procedure
terminates,
an alternating path can be
discovered by the:
- "Breakthrough" test
"Breakthrough" test:
- Find a labeled
vertex ∈ Y
that is
not incident (connected) to
an edge ∈ matching M
- If you can find such a vertex,
then tracing the
labels backward will
give you a
alternating path
- If you cannot find such a vertex, then the current matching is maximal (i.e., cannot be improved)
- If you can find such a vertex,
then tracing the
labels backward will
give you a
alternating path
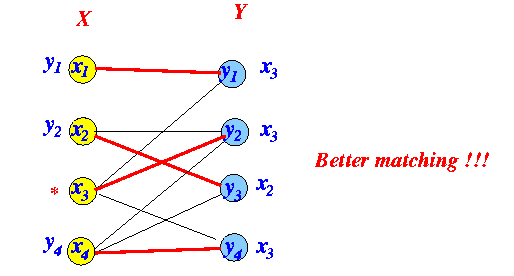
Example:
How to find the alternating path:
Trace the labels backwards to the * node Flip the edges in the alternating path 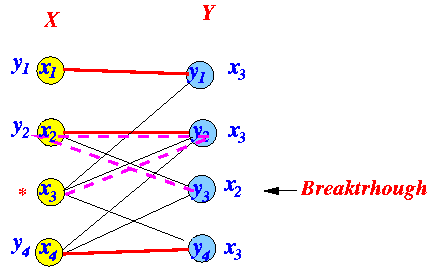
- Label the
first vertex xi
∈ X
that is not in the matching
with the
label
*:
- Bi-partite graph:
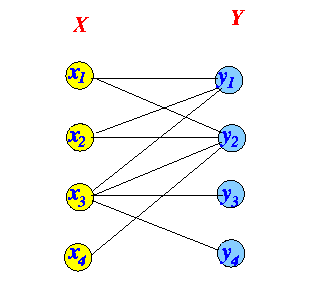
- Initial matching:
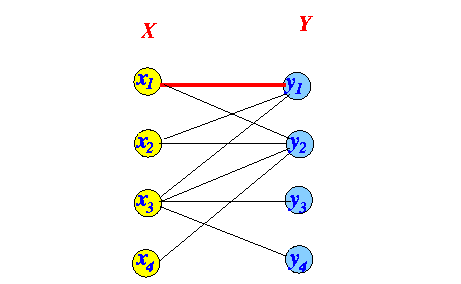
- Iteration 1: Labeling
Odd-edge: use edges ∉ matching Even-edge: use edges ∈ matching 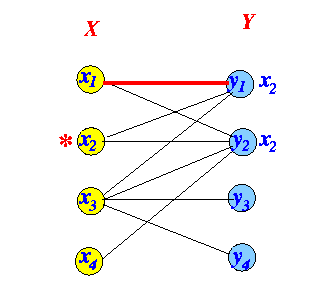
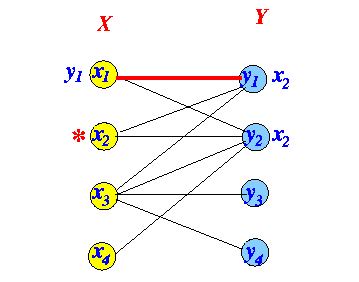
- Check for breakthrough:
Breakthrough test Alternating path 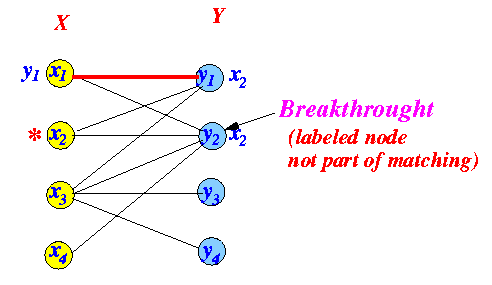
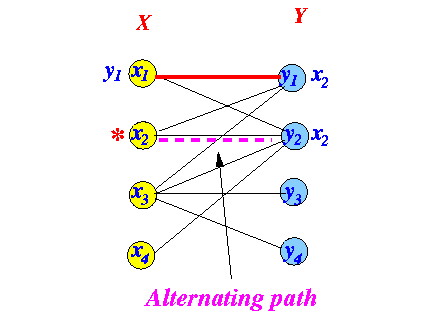
Improved matching:
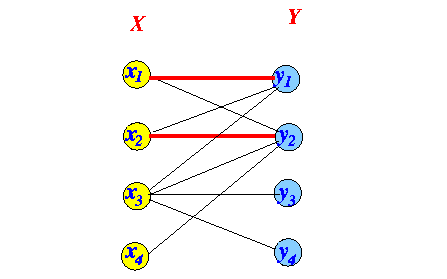
- Iteration 2:
Labeling algorithm
Odd-edge: use edges ∉ matching Even-edge: use edges ∈ matching 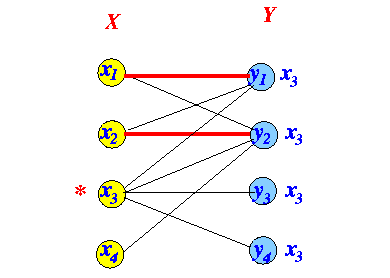
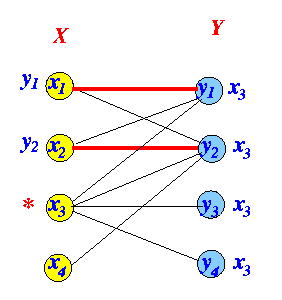
- Check for breakthrough:
Breakthrough test Alternating path 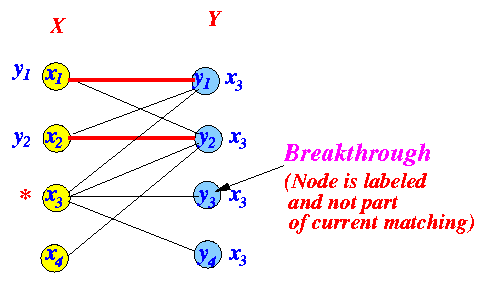
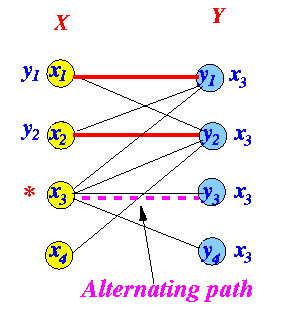
Improved matching:
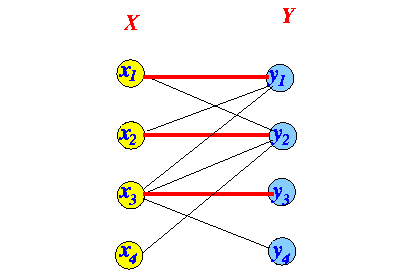
- Iteration 3:
Labeling algorithm
Odd-edge: use edges ∉ matching Even-edge: use edges ∈ matching Odd-edge: use edges ∉ matching Even-edge: use edges ∈ matching 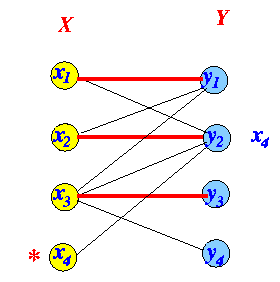
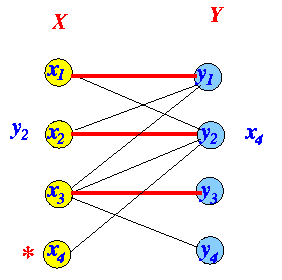
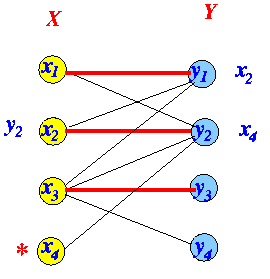
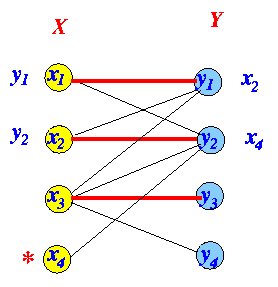
- Check for breakthrough:
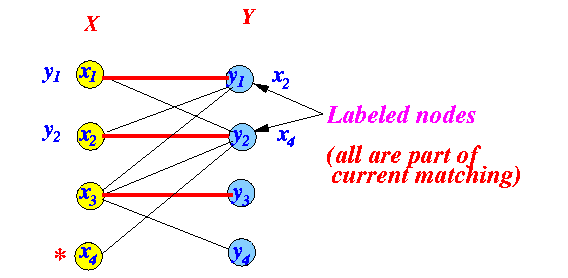
Ends without a breakthrough
- Maximal matching:

- Note:
- According to the Marriage Theorem,
when there are
some node ∈ X
cannot be matched,
then:
- There is a subset of k men that knows < k women
In this example, the value of k = 3 (take some time to determine this :))
- $64,000 question:
- Can you find a subset of 3 men that knows 2 women in the above graph ???
Answer to the $64,000 question:
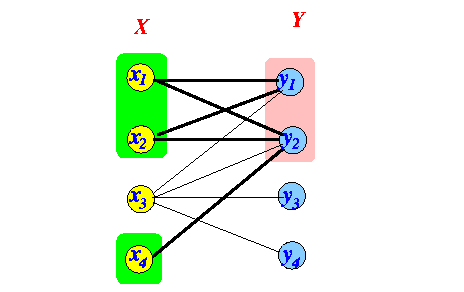
- According to the Marriage Theorem,
when there are
some node ∈ X
cannot be matched,
then: