- Psuedo code of remove(k):
Integer remove(Key k) { Entry e; Node p; /* ----------------------- Find k to remove ----------------------- */ e = keySearch(k); /* ======================= Check if k exists... ======================= */ if ( e == null ) { return(null); // Not found, nothing to delete... } /* ========================= We found the entry =============== */ Entry Old = e; // Remember the old value (to return it) /* ------------------------------ Step 1: remove entry e ------------------------------ */ p = node that contains entry e; if ( p == a leaf node ) { Delete entry e from p; // Note: this requires moving array elements } else /* Delete entry from internal node */ { /* ------------------------------- Replace e with e's successor ------------------------------- */ succ = successor entry of the deleted entry e; q = node that contains the succ entry; Replace entry e (in node p) with "succ" entry; Delete the succ entry from node q; // Note: this requires moving array elements p = q; } /* *********************************************** Handle a possible underflow situation *********************************************** */ if ( p is empty ) { handleUnderflow(p, null); // This is a recursive routine ! // The second parameter is a subtree that hangs under // the underflow node (the red reference in my figures) } return old.value; // Return }
- Java code:
public Integer remove(String k) { Entry e; Node p; int pos; /* ----------------------- Find k to remove ----------------------- */ e = keySearch(k); /* ======================= Check if k exists... ======================= */ if ( e == null ) { return(null); // Not found, nothing to delete... } /* ========================= We found the entry =============== */ Entry old = e; // Save for return value /* ---------------------------------------------------- Note: searchEndPos = node containing entry e ---------------------------------------------------- */ p = searchEndPos; /* ---------------------------------------------------- Find position of e inside p: p --> | T0 | e0 | T1 | e1 | T2 | e2 | T3 | Which of the e? is e ???? ---------------------------------------------------- */ for ( pos = 0; pos < 3; pos++ ) if ( p.e[pos] == e ) break; /* ---------------------------------------------------- Delete entry e from 2,4-tree ---------------------------------------------------- */ if ( p.child[0] == null /* ====> leaf node */ ) { /* ================================================== Delete entry e from a leaf node Note: this is done by MOVING right most entries into the slot containing e !!! ================================================== */ for ( int i = pos; i < 2; i++ ) p.e[i] = p.e[i+1]; p.e[2] = null; // The right most entry is for sure null ! } else { /* ------------------------------------------------ Non-leaf: 1. replace e with e's successor ------------------------------------------------ */ Node q; /* ------------------------------------------------ Use q to traverse to p's successor ------------------------------------------------ */ q = p.child[pos+1]; // Go right while ( q.child[0] != null ) q = q.child[0]; // Go left all the way down. /* ------------------------------------------------ Replace e by succ ------------------------------------------------ */ p.e[pos] = q.e[0]; // Replace e by e's successor /* ============================================== Delete succ from q (succ is always at pos 0) ============================================== */ for ( int i = 0; i < 2; i++ ) // Delete e's successor in q q.e[i] = q.e[i+1]; q.e[2] = null; /* ----------------------------------------------------- The target entry is now q ----------------------------------------------------- */ p = q; // node where entry was deleted } /* ********************************************************* Check for underflow situation in delete target location ********************************************************* */ if ( p.e[0] == null /* <===> node is empty */ ) { handleUnderflow(p, null); // Node p is empty // Second parameter is a subtree // hung under p } return old.value; // Return old value }
- Psuedo code of handleUnderflow(Node p):
/* ------------------------------------------------------- handleUnderflow(p, Z): handle the overflow condition in node p (p = empty !) Z = subtree that is left hanging when p became empty ------------------------------------------------------- */ void handleUnderflow(Node p, Node Z) { /* ---------------------------- Check if p is the root ---------------------------- */ if ( p == root ) { root = Z; // The subtree is the new tree !! return; // DONE ! } /* =================================================== Gather information before transfer or merge =================================================== */ Node parent; int pos; parent = p.parent; pos = index of subtree p in parent; // pos = 0, 1, 2 /* ------------------------------------------------------------- The meaning of pos: p's parent --> | C0 | e0 | C1 | e1 | C2 | e2 | C3 | ^ ^ ^ ^ | | | | if: C0==p C1==p C2==p C3==p then: pos=0 pos=1 pos=2 pos=3 -------------------------------------------------------------- */ /* ------------------------------------------------------------- Try: TRANSFER against your right sibling ------------------------------------------------------------- */ if ( p has a right sibling && p's right sibling has >= 2 entries ) { /* ------------------------------------- Transfer with right sibling See: click here ------------------------------------- */ R_Sibling = p's right sibling node; Perform this transfer: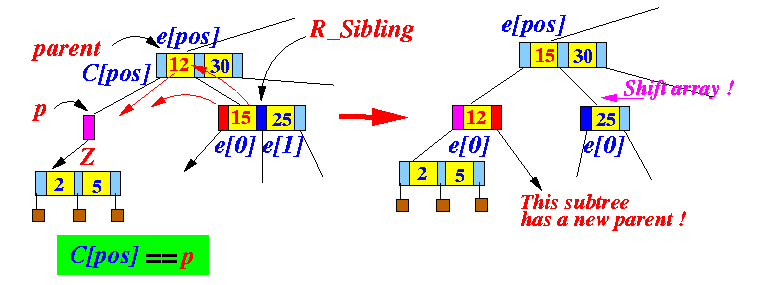 return; // DONE...
}
/* -------------------------------------------------------------
Solve underflow with a TRANSFER against your left sibling
------------------------------------------------------------- */
else if ( p has a left sibling && p's left sibling has >= 2 entries )
{
/* -------------------------------------
Transfer with left sibling
See: click here
------------------------------------- */
L_Sibling = p's left sibling node;
Perform this transfer:
return; // DONE...
}
/* -------------------------------------------------------------
Solve underflow with a TRANSFER against your left sibling
------------------------------------------------------------- */
else if ( p has a left sibling && p's left sibling has >= 2 entries )
{
/* -------------------------------------
Transfer with left sibling
See: click here
------------------------------------- */
L_Sibling = p's left sibling node;
Perform this transfer:
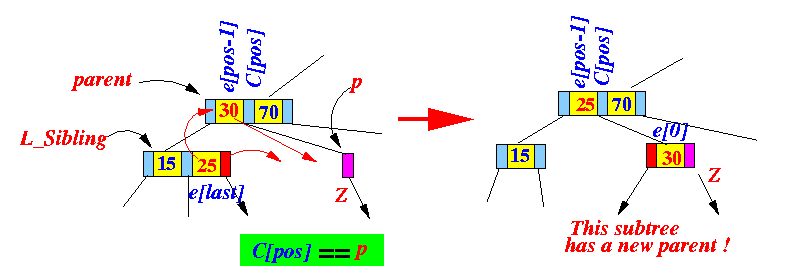 return; // DONE...
}
/* -------------------------------------------------------------
Solve underflow with a MERGE with your right sibling
------------------------------------------------------------- */
else if ( p.right_sibling != null )
{
/* ---------------------------
Merge with right sibling
See: click here
---------------------------*/
R_Sibling = p's right sibling node;
Perform this merge operation:
return; // DONE...
}
/* -------------------------------------------------------------
Solve underflow with a MERGE with your right sibling
------------------------------------------------------------- */
else if ( p.right_sibling != null )
{
/* ---------------------------
Merge with right sibling
See: click here
---------------------------*/
R_Sibling = p's right sibling node;
Perform this merge operation:
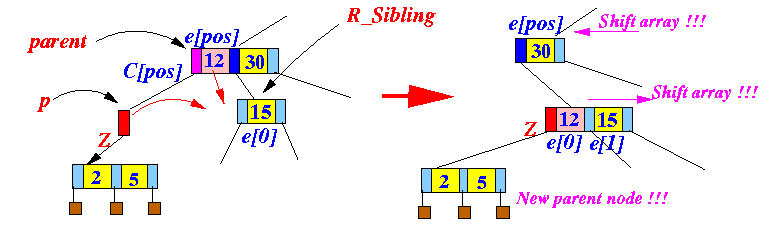 if ( parent become empty )
handleUnderflow(parent, R_Sibling);
}
else
{
/* ---------------------------
Merge with left sibling
See: click here
---------------------------*/
L_Sibling = p's left sibling node;
Perform this merge operation:
if ( parent become empty )
handleUnderflow(parent, R_Sibling);
}
else
{
/* ---------------------------
Merge with left sibling
See: click here
---------------------------*/
L_Sibling = p's left sibling node;
Perform this merge operation:
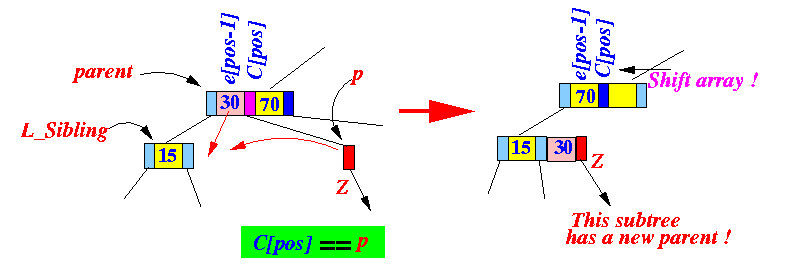 if ( parent become empty )
handleUnderflow(parent, L_Sibling);
}
}
if ( parent become empty )
handleUnderflow(parent, L_Sibling);
}
}
- Java code:
public void handleUnderflow(Node p, Node Z) { /* ================================================ Check if the root node is empty Note: This is a base case of the recursion.... ================================================ */ if ( p == root ) { root = Z; // Delete the empty root node p return; } /* =================================================== Gather information before transfer or merge =================================================== */ Node parent; int pos; parent = p.parent; for ( pos = 0; pos < 4; pos++ ) { if ( parent.child[pos] == p ) break; } /* ------------------------------------------------------------- The meaning of pos: p's parent --> | C0 | e0 | C1 | e1 | C2 | e2 | C3 | ^ ^ ^ ^ | | | | if: C0==p C1==p C2==p C3==p then: pos=0 pos=1 pos=2 pos=3 -------------------------------------------------------------- */ /* ------------------------------------------------------------- TRY a TRANSFER with your RIGHT sibling ------------------------------------------------------------- */ if ( (pos <= 2 && parent.child[pos+1] != null) /* p has a right sibling */ && parent.child[pos+1].e[1] != null /* R sibling has >= 2 entries */) { Node R_sibling = parent.child[pos+1];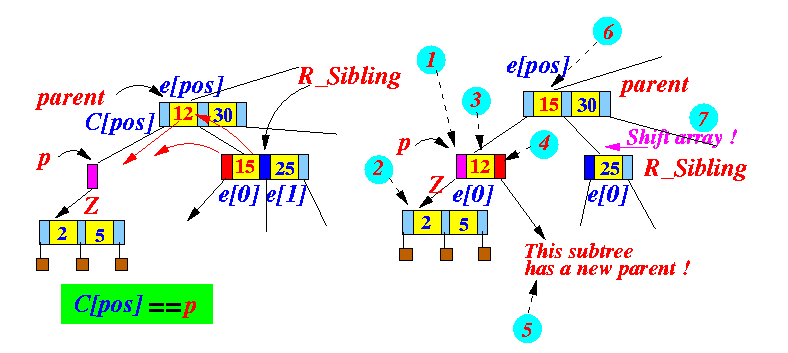 p.child[0] = Z; // (1)
if ( Z != null ) Z.parent = p; // (2)
p.e[0] = parent.e[pos]; // (3)
p.child[1] = R_sibling.child[0]; // (4)
if ( p.child[1] != null ) // (5) This subtree
p.child[1].parent = p; // has a new parent !!!
parent.e[pos] = R_sibling.e[0]; // (6) Move sibling entry to parent
/* ===================================
Delete e[0] in R_sibling
=================================== */
for ( int i = 0; i < 2; i++ ) // (7) ... accomplish by shifting
{
R_sibling.e[i] = R_sibling.e[i+1];
R_sibling.child[i] = R_sibling.child[i+1];
}
R_sibling.child[2] = R_sibling.child[3]; // Move child[3]
R_sibling.e[2] = null; // e[2] is now empty
R_sibling.child[3] = null; // child[3] is now empty
return; // Done
}
/* -------------------------------------------------------------
TRY a TRANSFER with your LEFT sibling
------------------------------------------------------------- */
else if ( pos > 0 /* p has a left sibling */
&& parent.child[pos-1].e[1] != null /* L sibling has >= 2 entries */)
{
Node L_sibling = parent.child[pos-1];
int last;
/* -------------------------------------
Find the last entry in L_sibling
------------------------------------- */
for ( last = 0; last < 3; last++ )
if ( L_sibling.e[last] == null )
break;
if ( last >= 3 || L_sibling.e[last] == null )
last--;
p.child[0] = Z; // (1)
if ( Z != null ) Z.parent = p; // (2)
p.e[0] = parent.e[pos]; // (3)
p.child[1] = R_sibling.child[0]; // (4)
if ( p.child[1] != null ) // (5) This subtree
p.child[1].parent = p; // has a new parent !!!
parent.e[pos] = R_sibling.e[0]; // (6) Move sibling entry to parent
/* ===================================
Delete e[0] in R_sibling
=================================== */
for ( int i = 0; i < 2; i++ ) // (7) ... accomplish by shifting
{
R_sibling.e[i] = R_sibling.e[i+1];
R_sibling.child[i] = R_sibling.child[i+1];
}
R_sibling.child[2] = R_sibling.child[3]; // Move child[3]
R_sibling.e[2] = null; // e[2] is now empty
R_sibling.child[3] = null; // child[3] is now empty
return; // Done
}
/* -------------------------------------------------------------
TRY a TRANSFER with your LEFT sibling
------------------------------------------------------------- */
else if ( pos > 0 /* p has a left sibling */
&& parent.child[pos-1].e[1] != null /* L sibling has >= 2 entries */)
{
Node L_sibling = parent.child[pos-1];
int last;
/* -------------------------------------
Find the last entry in L_sibling
------------------------------------- */
for ( last = 0; last < 3; last++ )
if ( L_sibling.e[last] == null )
break;
if ( last >= 3 || L_sibling.e[last] == null )
last--;
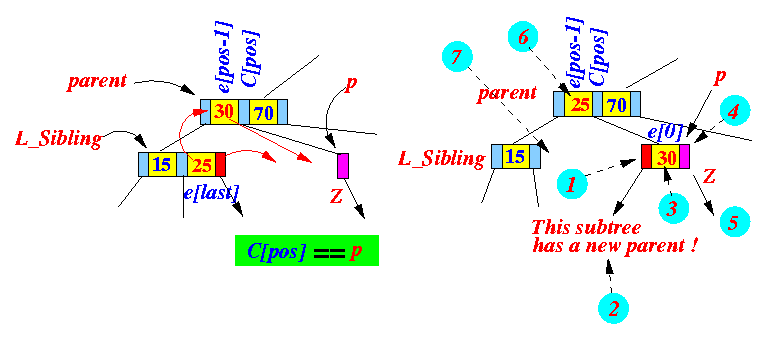 p.child[0] = L_sibling.child[last+1]; // (1)
if ( p.child[0] != null ) // (2) This subtree has a new parent
p.child[0].parent = p;
p.e[0] = parent.e[pos-1]; // (3) Transfer parent's entry
p.child[1] = Z; // (4) Hang Z
if ( Z != null ) Z.parent = p; // (5)
parent.e[pos-1] = L_sibling.e[last]; // (6) Move sibling entry to parent
/* ===================================
Delete e[lst] in L_sibling
=================================== */
L_sibling.e[last] = null; // (7)
L_sibling.child[last+1] = null;
return; // Done
}
/* -------------------------------------------------------------
TRY a MERGE with your RIGHT sibling
------------------------------------------------------------- */
else if ( pos != 3 /* No Right sibling possible */
&& parent.child[pos+1] != null /* There is a right sibling */)
{
Node R_sibling = parent.child[pos+1]; // R_sibling has ONLY 1 entry !
p.child[0] = L_sibling.child[last+1]; // (1)
if ( p.child[0] != null ) // (2) This subtree has a new parent
p.child[0].parent = p;
p.e[0] = parent.e[pos-1]; // (3) Transfer parent's entry
p.child[1] = Z; // (4) Hang Z
if ( Z != null ) Z.parent = p; // (5)
parent.e[pos-1] = L_sibling.e[last]; // (6) Move sibling entry to parent
/* ===================================
Delete e[lst] in L_sibling
=================================== */
L_sibling.e[last] = null; // (7)
L_sibling.child[last+1] = null;
return; // Done
}
/* -------------------------------------------------------------
TRY a MERGE with your RIGHT sibling
------------------------------------------------------------- */
else if ( pos != 3 /* No Right sibling possible */
&& parent.child[pos+1] != null /* There is a right sibling */)
{
Node R_sibling = parent.child[pos+1]; // R_sibling has ONLY 1 entry !
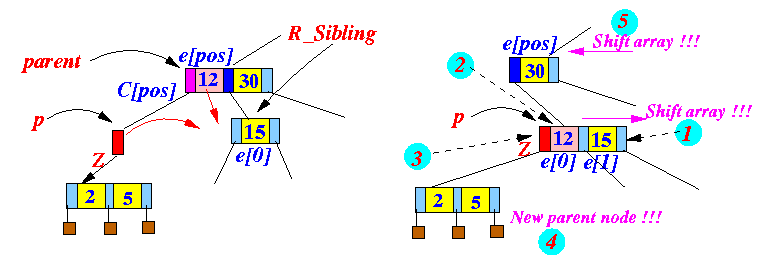 R_sibling.child[2] = R_sibling.child[1]; // (1) Move child[0] e[0] child[1]
R_sibling.e[1] = R_sibling.e[0];
R_sibling.child[1] = R_sibling.child[0];
R_sibling.e[0] = parent.e[pos]; // (2) Transfer parent's entry
R_sibling.child[0] = Z; // (3) Hang Z
if ( Z != null ) // (4) Subtree has a new parent
Z.parent = R_sibling;
/* ======================================
Delete parent.e[pos] in parent node
====================================== */
for ( int i = pos; i < 2; i++ ) // (5) accomplished by shift array
{
parent.child[i] = parent.child[i+1];
parent.e[i] = parent.e[i+1];
}
parent.child[2] = parent.child[3];
parent.e[2] = null;
parent.child[3] = null;
/* ===============================================
Check if parent node is empty....
=============================================== */
if ( parent.e[0] == null )
handleUnderflow(parent, R_sibling);
}
else /* ***** pos == 3, we MUST merge LEFT ... ****** */
{
Node L_sibling = parent.child[pos-1]; // L_sibling has 1 entry !
R_sibling.child[2] = R_sibling.child[1]; // (1) Move child[0] e[0] child[1]
R_sibling.e[1] = R_sibling.e[0];
R_sibling.child[1] = R_sibling.child[0];
R_sibling.e[0] = parent.e[pos]; // (2) Transfer parent's entry
R_sibling.child[0] = Z; // (3) Hang Z
if ( Z != null ) // (4) Subtree has a new parent
Z.parent = R_sibling;
/* ======================================
Delete parent.e[pos] in parent node
====================================== */
for ( int i = pos; i < 2; i++ ) // (5) accomplished by shift array
{
parent.child[i] = parent.child[i+1];
parent.e[i] = parent.e[i+1];
}
parent.child[2] = parent.child[3];
parent.e[2] = null;
parent.child[3] = null;
/* ===============================================
Check if parent node is empty....
=============================================== */
if ( parent.e[0] == null )
handleUnderflow(parent, R_sibling);
}
else /* ***** pos == 3, we MUST merge LEFT ... ****** */
{
Node L_sibling = parent.child[pos-1]; // L_sibling has 1 entry !
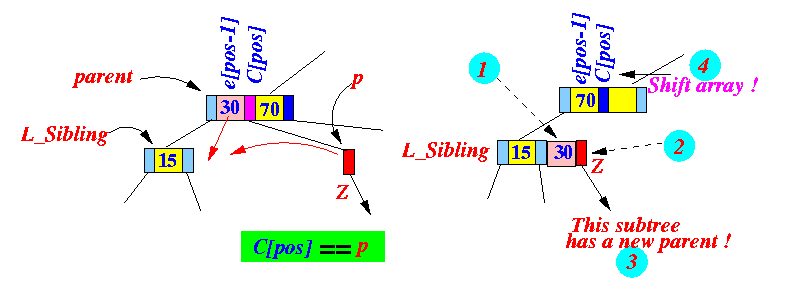 L_sibling.e[1] = parent.e[pos-1]; // (1) Transfer parent's entry
L_sibling.child[2] = Z; // (2) Hang Z
if ( Z != null ) // (3) This subtree has a new parent
Z.parent = L_sibling;
/* ======================================
Delete parent.e[pos] in parent node
====================================== */
for ( int i = pos-1; i < 2; i++ ) // (4) Shift array
{
parent.e[i] = parent.e[i+1];
parent.child[i+1] = parent.child[i+2];
}
parent.e[2] = null;
parent.child[3] = null;
/* ===============================================
Check if parent node is empty....
=============================================== */
if ( parent.e[0] == null )
handleUnderflow(parent, L_sibling);
}
}
L_sibling.e[1] = parent.e[pos-1]; // (1) Transfer parent's entry
L_sibling.child[2] = Z; // (2) Hang Z
if ( Z != null ) // (3) This subtree has a new parent
Z.parent = L_sibling;
/* ======================================
Delete parent.e[pos] in parent node
====================================== */
for ( int i = pos-1; i < 2; i++ ) // (4) Shift array
{
parent.e[i] = parent.e[i+1];
parent.child[i+1] = parent.child[i+2];
}
parent.e[2] = null;
parent.child[3] = null;
/* ===============================================
Check if parent node is empty....
=============================================== */
if ( parent.e[0] == null )
handleUnderflow(parent, L_sibling);
}
}
- Example Program:
(Demo above code)

- The Tree24.java Prog file: click here
- The Node.java Prog file: click here
- The Entry.java
Prog file:
click here
- A test program TestProg.java Prog file: click here
How to run the program:
- Right click on link(s) and
save in a scratch directory
- To compile: javac TestProg.java
- To run: java TestProg
Sample output:
Legend: red denotes the next deleted entry darkred denotes the entries involved in op darkgreen shows when the involved entries end up 2:((m,6),(-),(-)) 3:((ka,6),(l,6),(-)) 1:((kb,6),(-),(-)) 0:((j,6),(k,6),(-)) 1:((h,8),(-),(-)) 2:((g,7),(-),(-)) 0:((e,5),(f,6),(-)) 0:((ba,6),(d,4),(i,9)) 1:((ca,6),(-),(-)) 1:((c,3),(-),(-)) 0:((bb,6),(-),(-)) 3:((b,2),(-),(-)) 2:((ae,6),(af,6),(-)) <--- will be replaced by (ae,6) 0:((ab,6),(ad,6),(ax,6)) 1:((ac,6),(-),(-)) 0:((a,1),(aa,6),(-)) ================================================================== == After remove(ad): 2:((m,6),(-),(-)) 3:((ka,6),(l,6),(-)) 1:((kb,6),(-),(-)) 0:((j,6),(k,6),(-)) 1:((h,8),(-),(-)) 2:((g,7),(-),(-)) 0:((e,5),(f,6),(-)) 0:((ba,6),(d,4),(i,9)) 1:((ca,6),(-),(-)) 1:((c,3),(-),(-)) 0:((bb,6),(-),(-)) 3:((b,2),(-),(-)) 2:((af,6),(-),(-)) 0:((ab,6),(ae,6),(ax,6)) 1:((ac,6),(-),(-)) 0:((a,1),(aa,6),(-)) <---- will TRANSFER with Left sibling ==================================================== Underflow !!!! ===> Transfer with L sibling ((a,1),(aa,6),(-)) == After remove(ac): 2:((m,6),(-),(-)) 3:((ka,6),(l,6),(-)) 1:((kb,6),(-),(-)) 0:((j,6),(k,6),(-)) 1:((h,8),(-),(-)) 2:((g,7),(-),(-)) 0:((e,5),(f,6),(-)) 0:((ba,6),(d,4),(i,9)) 1:((ca,6),(-),(-)) 1:((c,3),(-),(-)) 0:((bb,6),(-),(-)) 3:((b,2),(-),(-)) 2:((af,6),(-),(-)) <---- will MERGE with Left sibling 0:((aa,6),(ae,6),(ax,6)) 1:((ab,6),(-),(-)) 0:((a,1),(-),(-)) ======================================== Underflow !!!! ===> MERGE with L sibling ((af,6),(-),(-)) == After remove(b): 2:((m,6),(-),(-)) 3:((ka,6),(l,6),(-)) 1:((kb,6),(-),(-)) 0:((j,6),(k,6),(-)) 1:((h,8),(-),(-)) 2:((g,7),(-),(-)) 0:((e,5),(f,6),(-)) 0:((ba,6),(d,4),(i,9)) 1:((ca,6),(-),(-)) 1:((c,3),(-),(-)) 0:((bb,6),(-),(-)) 2:((af,6),(ax,6),(-)) 0:((aa,6),(ae,6),(-)) 1:((ab,6),(-),(-)) 0:((a,1),(-),(-))