Priority queue
- A priority queue is a
data structure where:
- The
stored
data items can be
ranked
by some field
rank in the
data
- The
dequeue( )
operation
will
always
remove the
item in the
priority queue that
has the
highest value
in the
rank field
|
- The priority queue is
important in
time critical
applications
Example:
- Select the
next job to
run
(pick the most urgent one)
- Select the
next patient to
treat...
|
|
Naive implementation #1 of
the priority queue
- A
naive implementation
of
the priority queue:
- Use an fixed size
array
-
Enqueue( )
must
make sure the
array is
sorted
all the time
(from large to
small)
-
Dequeue( )
removes the
first element
in the array
|
- Example: the
enqueue( ) operation
Priority queue:
+---+---+---+---+---+---+---+---+---+
| 9 | 7 | 6 | 3 | 2 | | | | |
+---+---+---+---+---+---+---+---+---+
enqueue(5):
---> shift these elements to right
+---+---+---+---+---+---+---+---+---+
| 9 | 7 | 6 | 5 | 3 | 2 | | | |
+---+---+---+---+---+---+---+---+---+
|
|
Naive implementation #1 of
the priority queue
- A
naive implementation
of
the priority queue:
- Use an fixed size
array
-
Enqueue( )
must
make sure the
array is
sorted
all the time
(from large to
small)
-
Dequeue( )
removes the
first element
in the array
|
- Example: the
dequeue( ) operation
Priority queue:
+---+---+---+---+---+---+---+---+---+
| 9 | 7 | 6 | 3 | 2 | | | | |
+---+---+---+---+---+---+---+---+---+
dequeue(): (returns 9)
<--- shift these elements to left
+---+---+---+---+---+---+---+---+---+
| 7 | 6 | 3 | 2 | | | | | |
+---+---+---+---+---+---+---+---+---+
|
|
Naive implementation #2 of
the priority queue
- Another
naive implementation
of
the priority queue:
- Use an fixed size
array
-
Enqueue( )
insert the element
at
the end
-
Dequeue( )
searches for the
largest element
and remove it.
|
- Example:
Priority queue:
+---+---+---+---+---+---+---+---+---+
| 7 | 5 | 9 | 2 | 6 | | | | |
+---+---+---+---+---+---+---+---+---+
enqueue(8):
+---+---+---+---+---+---+---+---+---+
| 7 | 5 | 9 | 2 | 6 | 8 | | | |
+---+---+---+---+---+---+---+---+---+
|
|
Naive implementation #2 of
the priority queue
- Another
naive implementation
of
the priority queue:
- Use an fixed size
array
-
Enqueue( )
insert the element
at
the end
-
Dequeue( )
searches for the
largest element
and remove it.
|
- Example:
Priority queue:
+---+---+---+---+---+---+---+---+---+
| 7 | 5 | 9 | 2 | 6 | | | | |
+---+---+---+---+---+---+---+---+---+
dequeue( ): (returns 9)
<--- all elements shifted to left
+---+---+---+---+---+---+---+---+---+
| 7 | 5 | 2 | 6 | | | | | |
+---+---+---+---+---+---+---+---+---+
|
|
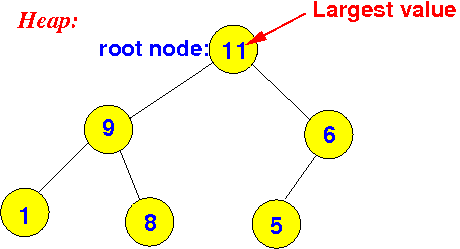
An efficient implementation
of the
priority queue
❮
❯