- Editing operations:
- A source (text) string
x[0..(n-1)]
- A target (destination) string
y[0..(m-1)]
- Possible editing operations
on strings:
- del(k): delete the
kth character
in
x[0..(n-1)]
Example:
0123456 del(3) abcdefg ----------> abcefg
- ins(c, k): insert
c as the
kth character
in
x[0..(n-1)]
Example:
0123456 ins(x,3) 01234567 abcdefg ------------> abcxdefg
- sub(c, k): replace
the
kth character
in
x[0..(n-1)] by
c
Example:
0123456 sub(x,3) 0123456 abcdefg ------------> abcxefg
- del(k): delete the
kth character
in
x[0..(n-1)]
- A source (text) string
x[0..(n-1)]
- Edit distance:
- The edit distance = the number of edit operations used to transform the source string x[0..(n-1)] into the target string y[0..(m-1)]
- Examples:
- Edit distance from:
man ⇒ moon
012 del(1) man -------------> mn 01 ins('o',2) mn -------------> mon 012 ins('o',2) mon -------------> moonEditDistance( "man", "moon" ) = 3
- Another way
to edit from:
man ⇒ moon is:
012 sub('o',1) man -------------> mon 012 ins('o',2) mon -------------> moonWhich gives EditDistance( "man", "moon" ) = 2
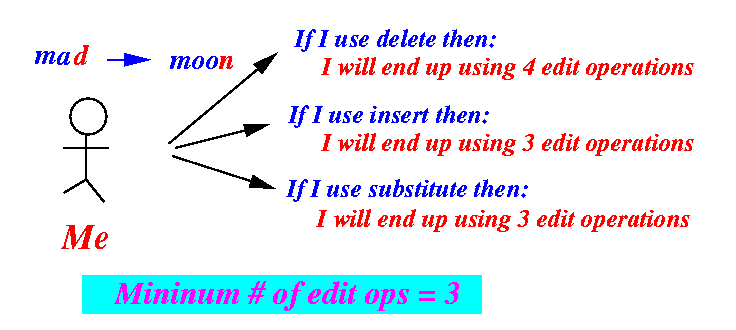
- Edit distance from:
man ⇒ moon
- Minimum edit distance between x[1..(n-1)] and y[0..(m-1)]:
- Minimum edit distance = minumum # edit operations used to transform source string x[0..(n-1)] to the target string y[0..(m-1)]
- Levenshtein distance:
- The minimum edit distance
(based
on the above 3 editing operations)
is
called: the
Levenshtein distance
Wikipedia page: click here
(Named after Vladimir Levenshtein)
- The minimum edit distance
(based
on the above 3 editing operations)
is
called: the
Levenshtein distance
- Finding a
divide and conquer
procedure to edit strings
----- part 1
- Case 1:
last characters are
equal
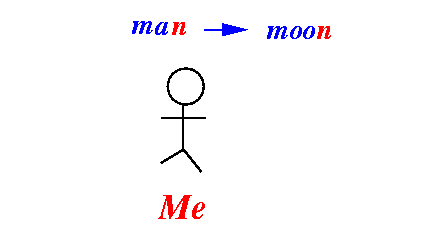
-
Divide and conquer strategy:
- Fact:
- I do not need to
perform any editing on
the last letters
- I can remove both letters.... (and have a smaller problem too !)
- I do not need to
perform any editing on
the last letters
- The following
smaller problem will
help me solve the
original problem:
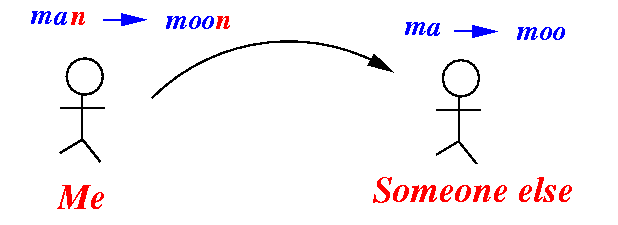
- How to solve the
orginal problem with
his solution:
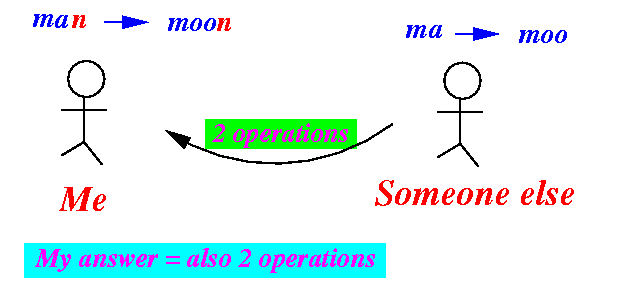
- Fact:
- Case 1:
last characters are
equal
- Finding a
divide and conquer
procedure to edit strings
----- part 2
- Case 2:
last characters are
not equal
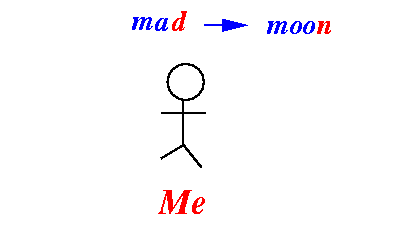
- Divide and conquer strategy:
- Fact:
- We must perform some editing operation of the last character position in the source string
- The editing operation
that can be performed on the
last letter position in
the source string
can be
one of the following:
- A delete operation:

- An insert operation:
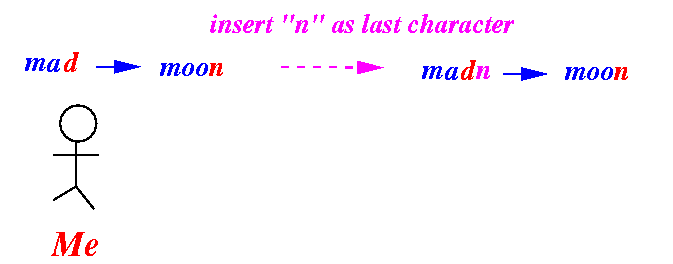
- A substitute operation:
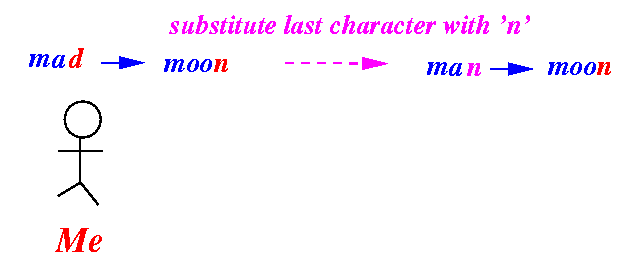
- A delete operation:
- We must find a
smaller (size) problem
to help us
solve the
original problem in
each case !!!
- The smaller problems
that will help us
solve the
original problem:
- If the
editing operation
is a delete operation:
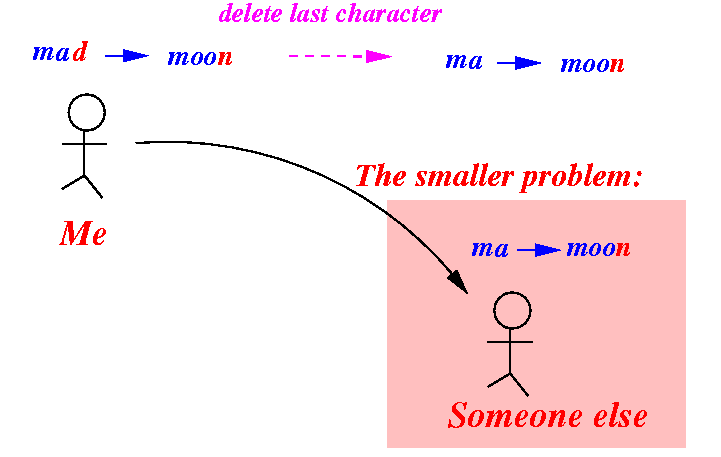
How to use the solution to solve the original problem:
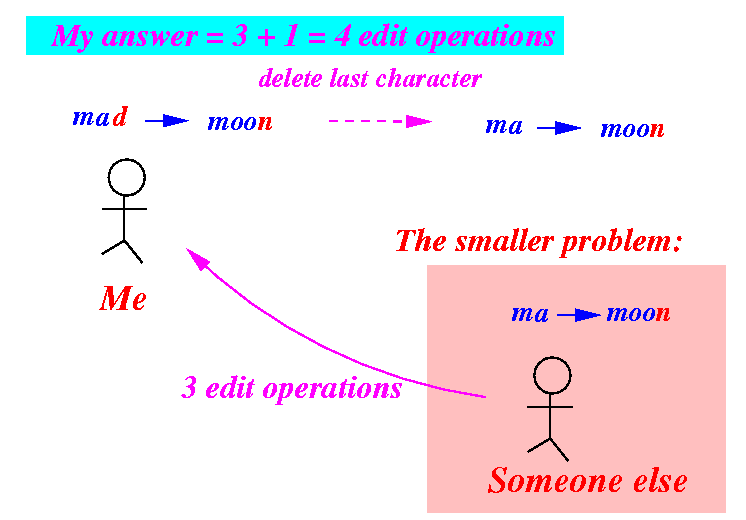
- If the
editing operation
is an insert operation:
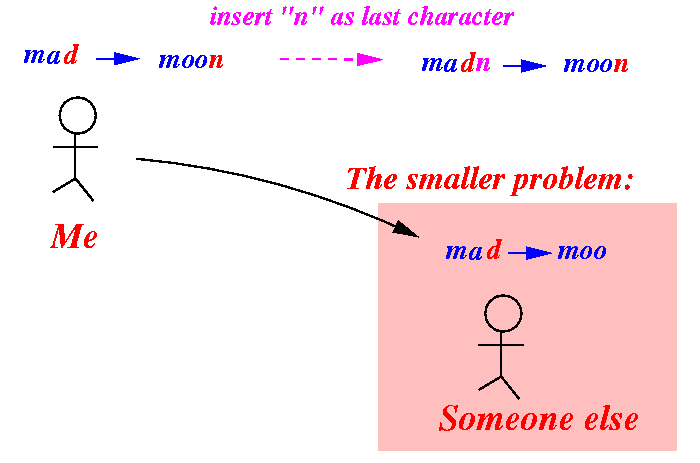
How to use the solution to solve the original problem:
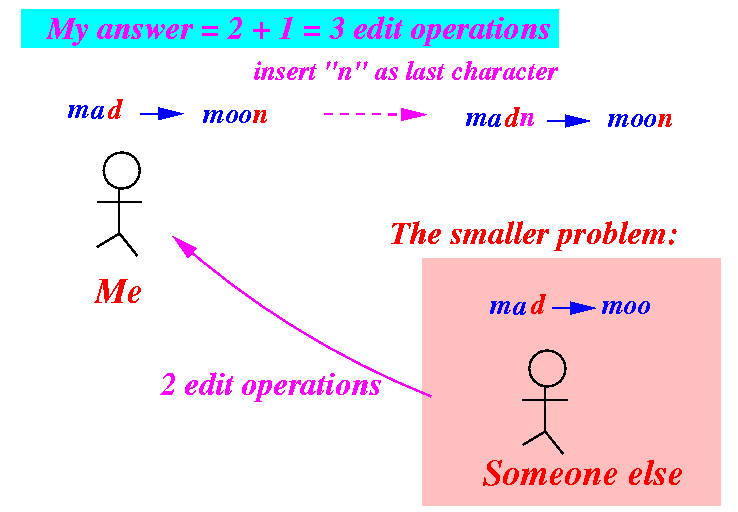
- If the
editing operation
is a substitute operation:
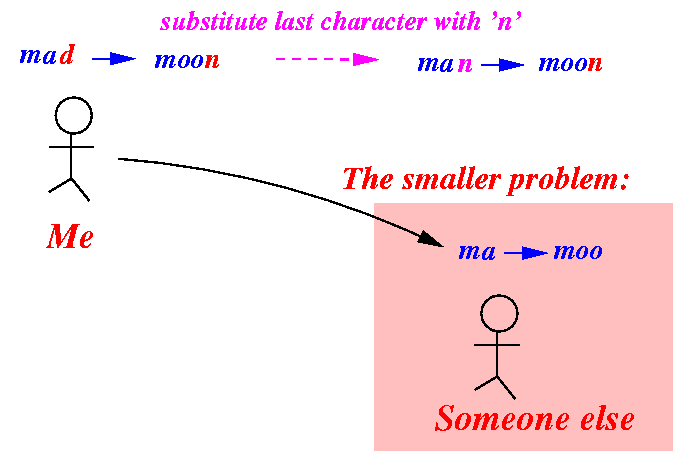
How to use the solution to solve the original problem:
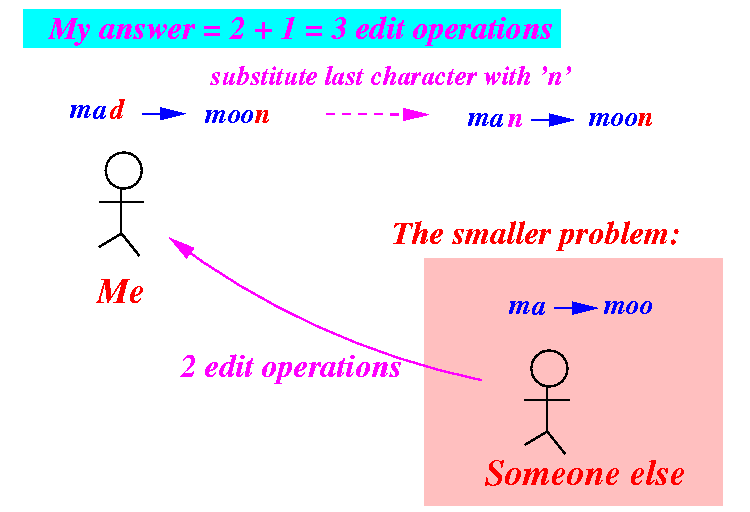
- If the
editing operation
is a delete operation:
- How to
obtain the
final answer:
- Fact:
- Case 2:
last characters are
not equal
- Define:
- T(i,j) =
the minumum # edit operations
needed to transform:
x[0..(i-1)] -----> y[0..(j-1)] (length=i) (length=j)
- T(i,j) =
the minumum # edit operations
needed to transform:
- The minimum edit distance problem:
- Given a source and
target string:
x = x[0..(n-1)] (length = n) y = y[0..(m-1)] (length = m)
- Find:
T(n,m)
- Given a source and
target string:
- Summary of the
divide and conquer procedure:
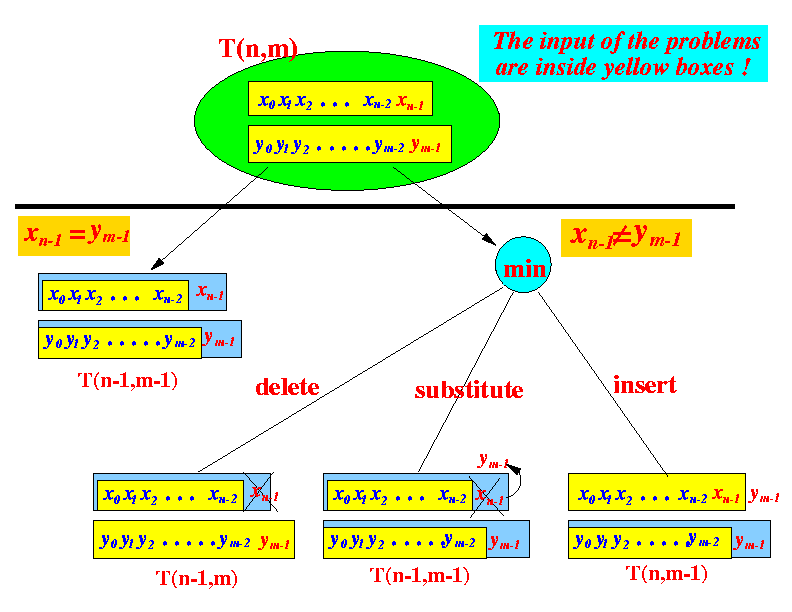
- Psuedo code
of the algorithm in the
above diagram:
T( x, y, n, m ) { // I will ignore the base cases for now.... /* ================================== The divide and conquer procedure =================================== */ if ( last char in x == last char in y ) { /* ------------------------------------ Last char's in strings are equal ------------------------------------ */ sol1 = T( x, y, n-1, m-1 ); // Solve smaller problem MySol = sol1 + 0; // Use solution to solve my problem return(MySol); } else { /* ------------------------------------------- Last char's in strings are NOT equal Divide: Try: delete, insert or substitute ------------------------------------------- */ sol1 = T(x, y, i-1, j); // Subproblem when edit oper is delete sol2 = T(x, y, i, j-1); // Subproblem when edit oper is insert sol3 = T(x, y, i-1, j-1); // Subproblem when edit oper is substit /* ------------------------------------------- Conquer: solve original problem using solution from smaller problems ------------------------------------------- */ MySol1 = sol1 + 1; // Cost of my solution if I used delete MySol2 = sol2 + 1; // Cost of my solution if I used insert MySol3 = sol3 + 1; // Cost of my solution if I usde substitute MySol = min( MySol1, MySol2, MySol3 ); return(MySol); } }
- The Base Case(s):
- If string x is
empty,
then only way to
edit x to y is:
- Insert the characters
of y
- We will need to use m insert operations
Example:
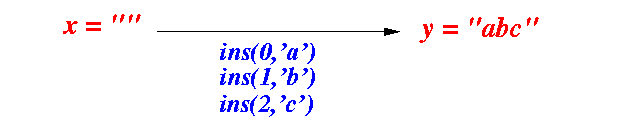
- Insert the characters
of y
- If string y is
empty,
then only way to
edit x to y is:
- Delete the characters
in x
- We will need to use n delete operations
Example:
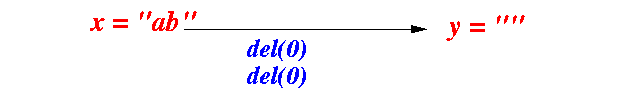
- Delete the characters
in x
- If string x is
empty,
then only way to
edit x to y is:
- Therefore:
T(0, m) = m (we need to insert m characters into x to get y) T(n, 0) = n (we need to delete n characters from x to get y)
- The recursive solution
(divide and conquer) is:
int MinEditDistance(String x, String y, int i, int j) { int sol1, sol2, sol3, MySol; /* --------------------------- Base cases --------------------------- */ if ( i == 0 ) // x = "" { return(j); // Uses j insertions } if ( j == 0 ) // y = "" { return(i); // Uses i deletions... } /* -------------------------------------------------- The other cases.... -------------------------------------------------- */ if ( x.charAt(i-1) == y.charAt(j-1) ) { /* ------------------------ Divide step ------------------------ */ sol1 = T(i-1, j-1); /* --------------------------------------- Conquer: solve original problem using solution from smaller problems --------------------------------------- */ MySol = sol1; // No edit necessary... return(MySol); } else { /* ------------------------ Divide step ------------------------ */ sol1 = T(i-1, j); // Try delete step as last sol2 = T(i, j-1); // Try insert step as last sol3 = T(i-1, j-1); // Try replace step as last /* --------------------------------------- Conquer: solve original problem using solution from smaller problems --------------------------------------- */ sol1 = sol1 + 1; sol2 = sol2 + 1; sol3 = sol3 + 1; /* --------------------------------------- Return min(sol1, sol2, sol3) --------------------------------------- */ if ( sol1 <= sol2 && sol1 <= sol3 ) MySol = sol1; if ( sol2 <= sol1 && sol2 <= sol3 ) MySol = sol3; if ( sol3 <= sol1 && sol3 <= sol2 ) MySol = sol3; return( MySol ); } }
- Example Program:
(Demo above code)

- Prog file: click here
How to run the program:
- Right click on link(s) and
save in a scratch directory
- To compile: javac MED.java
- To run: java MED
Sample output:
String x = man String y = moon Min. Edit Distance = 2
String x = mad String y = moon Min. Edit Distance = 3
- The beginner's way to
obtain a non-recursive (bottom-up)
Dynamic Programming solution is:
- Re-write the recursive program
into a program that uses
memoization
- Look at how the
array (table) variables are
updated
- Specifically:
find the statements used to
compute the
array variable that
is used to
store the
value of the computed solution
by the function call
- In the "Min. Edit distance" method, the method call MinEditDistance(x,y,i,j) will be stored in the array variable T[i][j]
- Specifically:
find the statements used to
compute the
array variable that
is used to
store the
value of the computed solution
by the function call
- Write an iterative method
that compute
T[i][j]
that runs the
indices
"with the data flow"
This direction is always from small to large:
for ( i = 0; i < x.length()+1; i++ ) for ( j = 0; j < y.length()+1; j++ ) compute T[i][j] = .....
- Re-write the recursive program
into a program that uses
memoization
- Advanced programming practice:
- With practice, we can skip the memoization step and write the non-recursive (bottom-up) dynamic programming solution using the recusive solution
Let's try to do that now....
- Consider the
Recursive Algorithm for
Min. Edit Distance:
int MinEditDistance(String x, String y, int i, int j) { int sol1, sol2, sol3, MySol; /* --------------------------- Base cases --------------------------- */ if ( i == 0 ) // x = "" { return(j); // Uses j insertions } if ( j == 0 ) // y = "" { return(i); // Uses i deletions... } /* -------------------------------------------------- The other cases.... -------------------------------------------------- */ if ( x.charAt(i-1) == y.charAt(j-1) ) { /* ------------------------ Divide step ------------------------ */ sol1 = T(i-1, j-1); /* --------------------------------------- Conquer: solve original problem using solution from smaller problems --------------------------------------- */ MySol = sol1; // No edit necessary... return(MySol); } else { /* ------------------------ Divide step ------------------------ */ sol1 = T(i-1, j); // Try delete step as last sol2 = T(i, j-1); // Try insert step as last sol3 = T(i-1, j-1); // Try replace step as last /* --------------------------------------- Conquer: solve original problem using solution from smaller problems --------------------------------------- */ sol1 = sol1 + 1; sol2 = sol2 + 1; sol3 = sol3 + 1; /* --------------------------------------- Return min(sol1, sol2, sol3) --------------------------------------- */ if ( sol1 <= sol2 && sol1 <= sol3 ) MySol = sol1; if ( sol2 <= sol1 && sol2 <= sol3 ) MySol = sol3; if ( sol3 <= sol1 && sol3 <= sol2 ) MySol = sol3; return( MySol ); } }
- Array definition:
- Since the method has
2 indices
(MinEditDistance(x, y,
i, j)),
we need to make a
2-dimensional array
to store the values for the
memoization (and the dynamic program):
int T[][] = new int[x.length()+1][y.length()+1];
- The dimensions of the
arrays are
x.length()+1 and
y.length()+1
because the values
of i and
j can
take on:
i = 0, 1, 2, .... x.length()+1 j = 0, 1, 2, ......... y.length()+1
- Since the method has
2 indices
(MinEditDistance(x, y,
i, j)),
we need to make a
2-dimensional array
to store the values for the
memoization (and the dynamic program):
- Base cases:
- The base cases
statements are:
/* --------------------------- Base cases --------------------------- */ if ( i == 0 ) // x = "" { return(j); // Uses j insertions } if ( j == 0 ) // y = "" { return(i); // Uses i deletions... }
- These statements
result
in the following values for
T[i][j]:
T[i][j] = j when i = 0 and T[i][j] = i when j = 0
- The non-recursive statements that
compute these same values are:
for ( j = 0; j <= y.length(); j++ ) T[0][j] = j; // T[i][j] = j when i = 0 for ( i = 0; i <= x.length(); i++ ) T[i][0] = i; // T[i][j] = i when j = 0
- The base cases
statements are:
- The other cases:
- The solution MySOl
of the function call
MinEditDistance(x, y, i, j)
will be stored in the array element
T[i][j]:
MySol <======> T[i][j]
- The statements used to
compute
the solution MySol are:
- In the then part:
if ( x.charAt(i-1) == y.charAt(j-1) ) { MySol = T(i-1, j-1); }
Because: T(i-1, j-1) is stored in T[i-1][j-1] MySol is stored in T[i][j] this would result in the following update: if ( x.charAt(i-1) == y.charAt(j-1) ) { T[i][j] = T[i-1][j-1]; }
- And in the else part:
sol1 = T(i-1, j); // Try delete step as last sol2 = T(i, j-1); // Try insert step as last sol3 = T(i-1, j-1); // Try replace step as last /* --------------------------------------- Conquer: solve original problem using solution from smaller problems --------------------------------------- */ sol1 = sol1 + 1; sol2 = sol2 + 1; sol3 = sol3 + 1; /* --------------------------------------- Return min(sol1, sol2, sol3) --------------------------------------- */ if ( sol1 <= sol2 && sol1 <= sol3 ) MySol = sol1; if ( sol2 <= sol1 && sol2 <= sol3 ) MySol = sol3; if ( sol3 <= sol1 && sol3 <= sol2 ) MySol = sol3;
Becomes: sol1 = T[i-1][j]; // Try delete step as last sol2 = T[i][j-1]; // Try insert step as last sol3 = T[i-1][j-1]; // Try replace step as last /* --------------------------------------- Conquer: solve original problem using solution from smaller problems --------------------------------------- */ sol1 = sol1 + 1; sol2 = sol2 + 1; sol3 = sol3 + 1; if ( sol1 <= sol2 && sol1 <= sol3 ) T[i][j] = sol1; if ( sol2 <= sol1 && sol2 <= sol3 ) T[i][j] = sol2; if ( sol3 <= sol1 && sol3 <= sol2 ) T[i][j] = sol3;
- In the then part:
- The solution MySOl
of the function call
MinEditDistance(x, y, i, j)
will be stored in the array element
T[i][j]:
- Notice
that the "data flow" direction
is as follows:
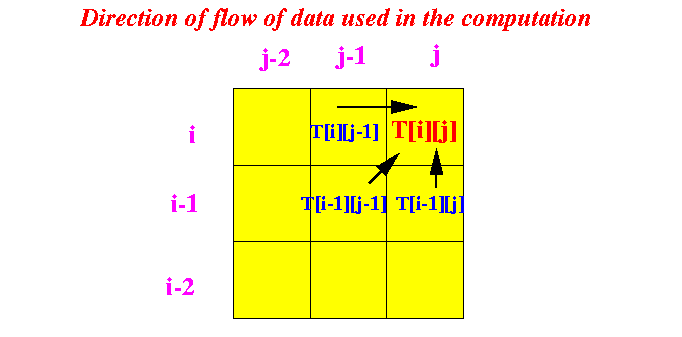
so you avoid using recursion if we compute the values T[i][j] in the following order:
for ( i = 0; i < x.length()+1; i++ ) for ( j = 0; j < y.length()+1; j++ ) { compute T[i][j] according to the recursive algorithm }
- Now put it together...
Botton-up Dynamic Programming for Min. Edit Distance:
static int[][] T; // Store the result of T(i,j) static int compT(String x, String y) { int sol1, sol2, sol3; int i, j; /* --------------------------- Base cases --------------------------- */ for ( i = 0; i <= x.length(); i++ ) T[i][0] = i; for ( j = 0; j <= y.length(); j++ ) T[0][j] = j; /* ------------------------ The other cases... ------------------------ */ for ( i = 1; i <= x.length(); i++ ) for ( j = 1; j <= y.length(); j++ ) { if ( x.charAt(i-1) == y.charAt(j-1) ) { sol1 = T[i-1][j-1]; T[i][j] = sol1; } else { /* ------------------------ Divide step ------------------------ */ sol1 = T[i-1][j]; // Try delete step as last step sol2 = T[i][j-1]; // Try insert step as last step sol3 = T[i-1][j-1]; // Try replace step as last step /* --------------------------------------- Conquer: solve original problem using solution from smaller problems --------------------------------------- */ sol1 = sol1 + 1; sol2 = sol2 + 1; sol3 = sol3 + 1; if ( sol1 <= sol2 && sol1 <= sol3 ) T[i][j] = sol1; if ( sol2 <= sol1 && sol2 <= sol3 ) T[i][j] = sol2; if ( sol3 <= sol1 && sol3 <= sol2 ) T[i][j] = sol3; } } /* ----------------------------- Return the final answer... ----------------------------- */ return(T[x.length()][y.length()]); }
- Example Program:
(Demo above code)

- Prog file: click here
- The subproblems that the
program solves are:
- L(i,j) where i = 1..n and j = 1..m
- So there are n × m
subproblems
Each subproblem can be solved with O(1) time (find the minimum of 3 numbers)
- Hence:
- running time = O(n × m)