- Purpose:
- A hash function maps a key (value) to an integer in the range [0..(N-1)]
- A hash function usually consists
of 2 parts:
- A hash code that
maps a key (value)
to an integer
(unbounded)
- A compression function that maps an arbitrary integer (value) to an integer in the range [0..(N-1)]
Graphically:
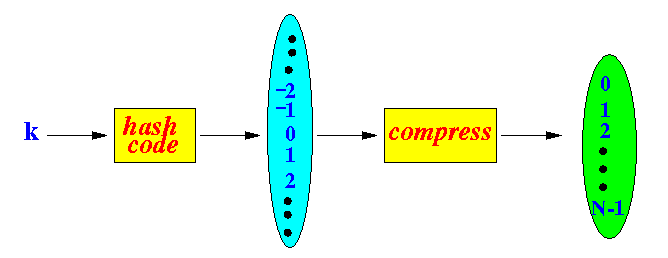
- A hash code that
maps a key (value)
to an integer
(unbounded)
- Property:
- The hash code should
avoid collisions
(I.e.: different keys should hash to different values)
- The hash code should map the same keys to the same value
- The hash code should
avoid collisions
- Example of a poor hash function:
- h(x) = the address of the object (variable) x
Reason:
- Consider these 2 objects:
- k1 = "abc"
- k2 = "abc"
- The different objects
k1 and
k2 have:
- different addresses
- But: the same key ("abc") !!!
Graphically depicted:
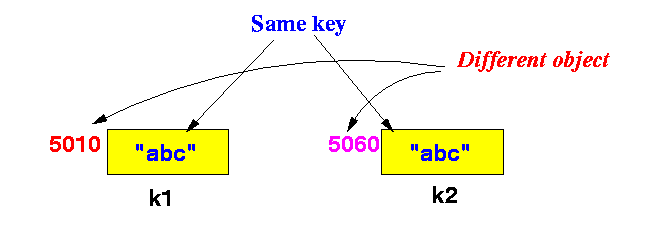
The hash function should map the objects k1 and k2 to the same hash value (because hash value must be based on the value of the key !)
- However,
because k1
and k1
are different objects,
they have
different memory addresses
- When using the address as hash function h(x), this map function will assign the objects k1 and k2 to different hash values !!!
- Overview common hash codes:
- Casting (converting) to integer (e.g.: byte → int and char → int)
- Summing
the components
(e.g.: fold a
double into an int)
- Polynomial hash codes (e.g.: String → int)
- Cyclic shift hash codes (e.g.: String → int)
- Converting byte and short to
integer:
- Use the cast operator (int)
(This operation will not change the value of the byte or short)
- Use the cast operator (int)
- Converting float to
integer:
- Use the cast operator (int)
(This operation will not change the value of the byte or short)
- Better:
because a float
representation uses 4 bytes
(just like integer), we can
use the bit pattern in the
float
as an integer
Example:
int x; float f; x = Float.floatToIntBits(f);
- Use the cast operator (int)
- Example Program:
(Demo above code)

- Prog file: click here
- Converting long and double values
to integer:
- Long values and
double values are
(both) represented using
8 bytes
- When a value of type long or double (8 bytes) is hashed to an integer (4 bytes), we can split the representation into 2 parts and sum the parts
- Long values and
double values are
(both) represented using
8 bytes
- Summing the 2 parts of a long:
static int hashCode(long x) { int p1, p2; p1 = (int) x; // lower 32 bits p2 = (int) (x >> 32); // upper 32 bits return(p1 + p2); }
- Summing the 2 parts of a double:
static int hashCode(double d) { int p1, p2; long x; x = Double.doubleToRawLongBits(d); // Use the bits as a long.... p1 = (int) x; // lower 32 bits p2 = (int) (x >> 32); // upper 32 bits return(p1 + p2); }
- Polynomial hsah codes
are used to hash
String typed keys
- String:
- A string is a
sequence of characters
encoded using
ASCII code
---
See: Wikipedia at
click here
(ASCII code is an integer code)
Example:
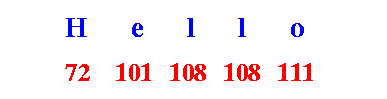
- A string is a
sequence of characters
encoded using
ASCII code
---
See: Wikipedia at
click here
- Caveat:
- The string Hello is
not the same as
Holle or
Holel, and so on.
- Therefore:
- Summing the
character code (values)
is not a good
hashing method for Strings
(Because different strings containing the same characters will hash to the same value)
- Summing the
character code (values)
is not a good
hashing method for Strings
- The string Hello is
not the same as
Holle or
Holel, and so on.
- Polynomial hash code:
- Given a string
s = "xk-1xk-2 ...
x0"
- h(s) = xk-1 × ak-1 + xk-2 × ak-2 + ... + x0 × a0
Example:
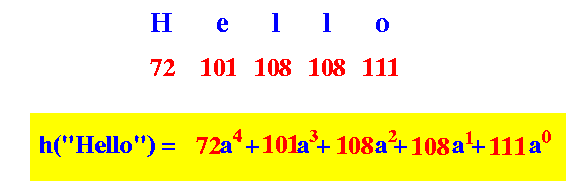
- Given a string
s = "xk-1xk-2 ...
x0"
- Implementation:
- Notice that:
h(s) = xk-1 × ak-1 + xk-2 × ak-2 + ... + x0 × a0 = x0 × a0 + x1 × a1 + + x2 × a2 + ... + xk-1 × ak-1 = x0 + x1 × a1 + + x2 × a2 + ... + xk-1 × ak-1 = x0 + a1 × (x1 + x2 × a1 + ... + xk-1 × ak-2) = x0 + a1 × (x1 + a1 × (x2 + ... + xk-1 × ak-2) ) ..... = x0 + a × (x1 + a × (x2 + a × ( ... + xk-3 + a × ( xk-2 + a × xk-1 ) ) ) ) - Repeated step:
- Multiply result by a
- Add the next digit to the right
- Psuedo code:
public static int hashCode(String s) { int i; int r = 0; char c; for (i = 0; i < s.length(); i++) { c = s.charAt(i); // process next character r = (int) c + a*r; // Cascaded evaluation of the polynoimal (classic trick) } return(r); }
- Notice that:
- Example Program:
(Demo above code)

- Prog file: click here
- The choice of the value of
a is important for a
spread of the
hash value
- Empirically found "good" values:
- 33,
37,
39,
41
(All prime numbers)
(In the test program, I used a = 100 to show the effect of the polynomial computation)
- 33,
37,
39,
41
- A cyclic shift hash code is
nothing more than a
polynomial hash code
using the
shift operation to perform a
multiplication
Example:
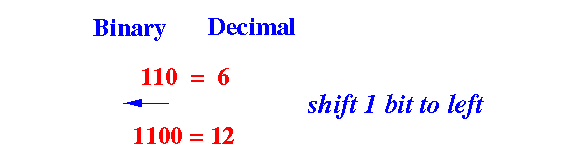
- Example: polynomial hash code with
a = 2 implemented with
a shift operator
public static int hashCode(String s) { int i; int r = 0; char c; for (i = 0; i < s.length(); i++) { c = s.charAt(i); // process next character r = (int) c + (r << 1); // Left shift 1 = multiply by 2 } return(r); }
- Example: polynomial hash code with
a = 3 implemented with
a shift operator
public static int hashCode(String s) { int i; int r = 0; char c; for (i = 0; i < s.length(); i++) { c = s.charAt(i); // process next character r = (int) c + ((r << 1) + r << 0)); // (2 + 1)r } return(r); }Faster (but approximate) implementation:
public static int hashCode(String s) { int i; int r = 0; char c; for (i = 0; i < s.length(); i++) { c = s.charAt(i); // process next character r = (int) c + ((r << 1) | r << 0)); // Bit-wise OR os faster than an addition } return(r); }
- Simplest compression function:
modulo N
Hash index = hashCode % N
- Advantage:
- Efficient
- Disadvantage:
- The ability to
spread
hash code is limited
(If the hash code produces value of the form p×N + q, all these value will be compressed to q)
- The ability to
spread
hash code is limited
- The MAD compression method:
Hash index = ( (a × hashCode + b) % p ) % N
with: p = prime number > N a = integer from range [1..(p-1)] b = integer from range [0..(p-1)]Note:
- To avoid
using negative indices
(which can result from
overflow),
we use:
Hash index = ( abs(a × hashCode + b) % p ) % N
- To avoid
using negative indices
(which can result from
overflow),
we use:
- Advantage:
- From Mathemical analysis (group theory), this compression function will spread integer (more) evenly over the range [0..(N-1)] if we use a prime number for p.
- Disadvantage:
- More complex
- The compression operation
will spread the
hash code over
all possible value
between [0 .. N]
when you use a
prime number
This is not so when you use a non-prime number
- Example 1:
use a non-prime p
----- hash index =
(3×k + 1) %
12) % 10
(notice 12 is divisble by 3)
any key / | \ / | \ (will result in some hash code) / | \ hash code x = 0 1 2 3 4 5 6 7 8 9 10 11 12 ... | compress V (3×x + 1) % 12) % 10 = 1 4 7 0 1 4 7 0 1 4 7 0 1 ... | | | | | | +------------+ +------------+ +------------+ repeat repeat repeatNotice that:
- Not every number in the
range [0..9] are used as
hash index !!!
- Result:
- More collisions !!!
- Not every number in the
range [0..9] are used as
hash index !!!
- Example 2:
(modulo operation with the
prime number 13)
----- hash index =
(3×k + 1) %
13) % 10
any key / | \ / | \ (will result in some hash code) / | \ hash code: k = 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15... | compress V (3×k + 1) % 13) % 10 = 1 4 7 0 0 3 6 9 2 2 5 8 1 1 4 7 ... | | +------------------------------------------------+ repeatNotice that:
- Every number in the range
[1..9]
are used as hash index !!!
Better spread !!!
- Every number in the range
[1..9]
are used as hash index !!!
- Program used to generate the MAD code:

- Prog file: click here