- Open addressing:
- In Open address, each bucket
stores
(upto) one entry
(i.e., one entry per
hash location/address)
- When the hash location is occupied, a specific search (probe) procedure is invoked to locate the searched key or an empty slot
- In Open address, each bucket
stores
(upto) one entry
(i.e., one entry per
hash location/address)
- Linear Probing:
- When a bucket i is
used, the
next bucket you will try is
bucket i+1
- The search can wrap around and continue from the start of the array.
- When a bucket i is
used, the
next bucket you will try is
bucket i+1
- Input keys: (the values associated with the keys
are omitted for brevity)
- 18, 41, 22, 44, 59, 32, 31, 73
- Hash array size: 13
Hash function: h(k) = k % 13
- 18, 41, 22, 44, 59, 32, 31, 73
- Insertions:
- insert key 18:
18 % 13 = 5

- insert key 41:
41 % 13 = 2

- insert key 22:
22 % 13 = 9

- insert key 59:
59 % 13 = 7
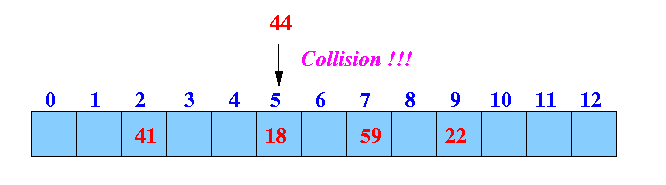
- insert key 44:
44 % 13 = 5 ------
collision !!!

Solution: search (= probe) for an empty slot in hash table:
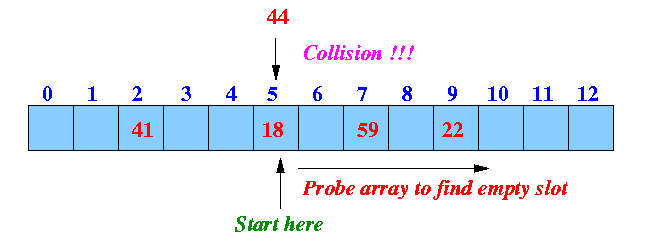
Simplest probing procedure: linear probing --- look in next slow
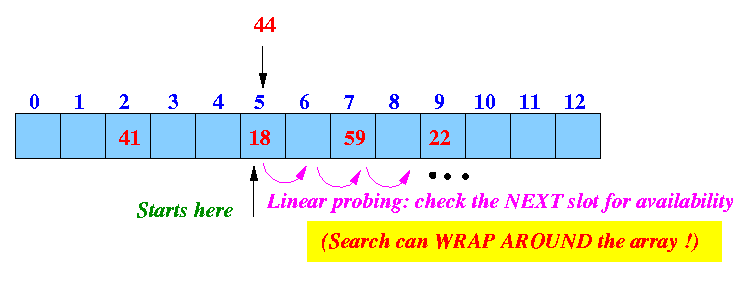
Result:

Note:
- Keys that hash to the
same hash bucket
(= array element)
will always
be clustered together
(= occupy consecutive array elements(
- But,
unrelated keys
can cluster !!!
Example:
- The unrelated key 59 and keys 18 and 44 has formed a cluster
- Keys that hash to the
same hash bucket
(= array element)
will always
be clustered together
(= occupy consecutive array elements(
- insert key 32:
32 % 13 = 6

Note:
- Bucket 6 is
used
- We keep looking for an empty bucket
to store the new key
- We found an (first) empty slot in bucket 8
- We keep looking for an empty bucket
to store the new key
- BTW, the cluster gets bigger (snow ball effect :-))
- Bucket 6 is
used
- insert key 31:
31 % 13 = 5

Note:
- Bucket 5 is
used
- We keep looking for an empty bucket
to store the new key
- We found an (first) empty slot in bucket 10
- We keep looking for an empty bucket
to store the new key
- Bucket 5 is
used
- insert key 73:
73 % 13 = 8

Note:
- Bucket 8 is
used
- We keep looking for an empty bucket
to store the new key
- We found an (first) empty slot in bucket 11
- We keep looking for an empty bucket
to store the new key
- Bucket 8 is
used
- insert key 18:
18 % 13 = 5
- Pseudo code for
linear probing:
start = HashValue( key ); // Start looking in the Hash location search_i = start; // Start here while ( bucket[sreach_i] != EMPTY /* not empty */ && "search did not wrap around" ) { search_i = (search_i + 1) % N; // Keep looking in the NEXT hash bucket }
- Notice:
- Increased occupancy level will increase the likelihood of collisions
- Lookup procedure for the key k
- i =
hash the key k to
find the bucket index b
- Starting at
bucket b,
look for the key k using the
same probing procedure
- There will be 3 possible outcomes:
- You find the key k:
- In this case, you can perform the operation on the entry.
- E.g.: return the value, update the value of delete the entry
- You find an empty slot
before you find the key k
- Then the key k is
not stored in the
hash table
- You return not found
- Then the key k is
not stored in the
hash table
- The search wrapped around
(you end up where you started):
- Then the hash table is
completely filled up and
the key k is
not stored in the
hash table
- You return not found
- Then the hash table is
completely filled up and
the key k is
not stored in the
hash table
- You find the key k:
- i =
hash the key k to
find the bucket index b
- Example: get(31)
- get(31):
find the hash index (location)
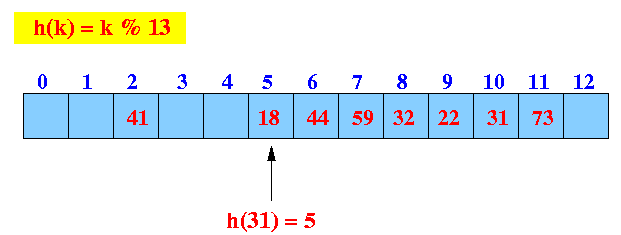
Start looking at location 5
- Linear probe procedure:
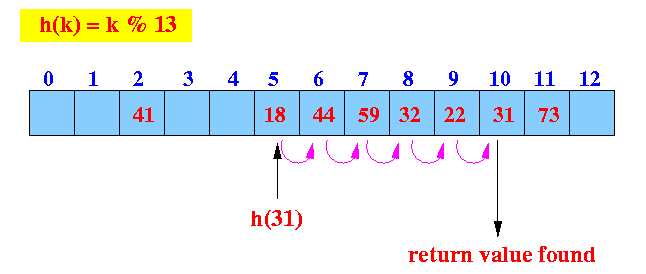
We found the key (31) ==> return found.
- get(31):
find the hash index (location)
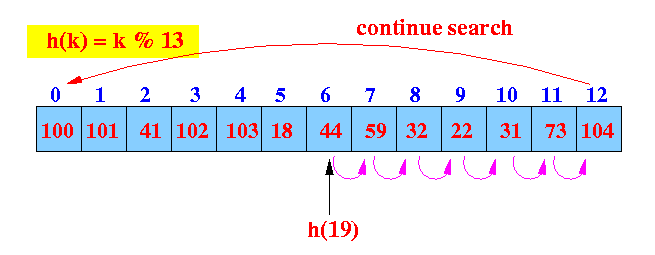
- Example: get(19)
- get(19):
find the hash index (location)
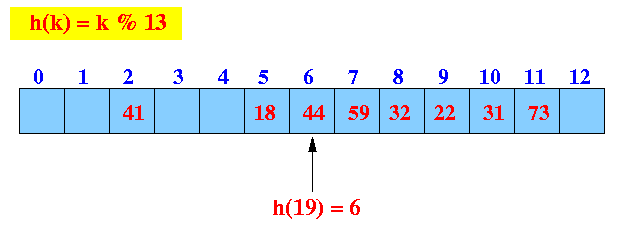
Start looking at location 6
- Linear probe procedure:
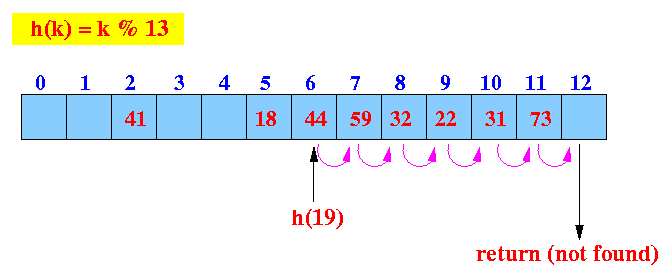
We reach an empty slow before finding the key 19.
Return not found !!!
- get(19):
find the hash index (location)
- Example: get(19)
in a full hash table
- get(19):
find the hash index (location)
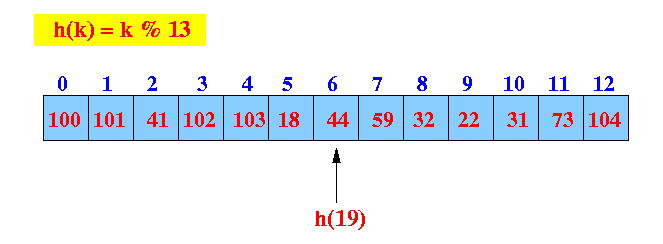
Start looking at location 6
- Linear probe procedure:
We reach the end, the search continues from the start of the array:
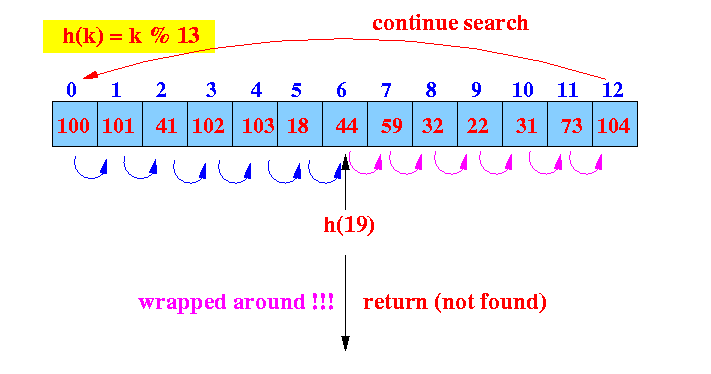
The search has wrapped around complete ==> key is not in the hash table.
Return not found !!!
- get(19):
find the hash index (location)
- Commonly used search procedures in
Hashing:
- Linear probing:
- The location for the
ith probe is
hashIndex + i
Graphically:
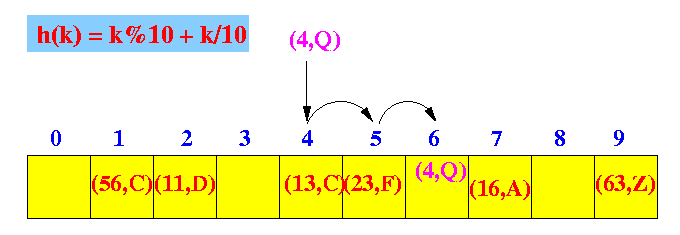
- The location for the
ith probe is
hashIndex + i
- Quadratic probing:
- The location for the
ith probe is
hashIndex + i2
Graphically:
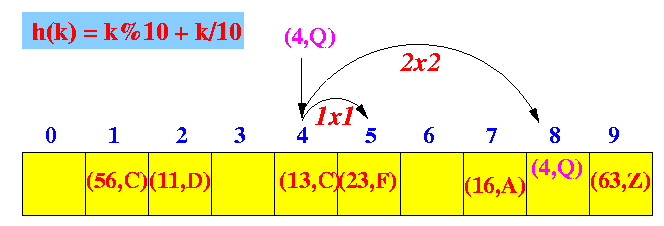
- The location for the
ith probe is
hashIndex + i2
- Double hashing:
- Uses 2 different hash functions:
h(k) and h2(k):
- h(k) is used to
find the hash location (hashIndex)
- h2(k) is used to probe
- h(k) is used to
find the hash location (hashIndex)
- The location for the
ith probe is
hashIndex + i × h2(k)
Graphically:
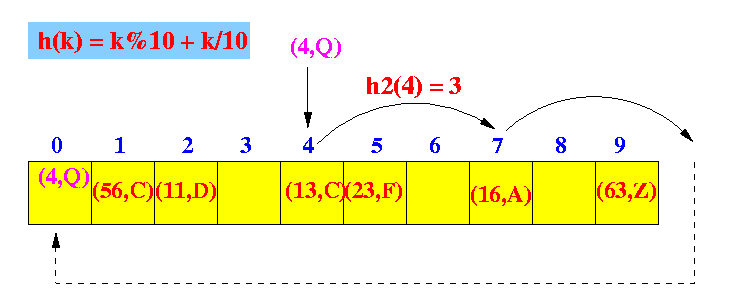
- The secondary hash function:
- Cannot produce
zero as hash result !
- Commonly used one:
- h2(k) = q − (k % q) (q = a prime number < N)
- Cannot produce
zero as hash result !
- Uses 2 different hash functions:
h(k) and h2(k):
- Linear probing:
- Pro's and con's:
- Linear probing:
- Simple to implement
- But can create
clusters
(series of occupied cells
of
unrelated keys)
Example:
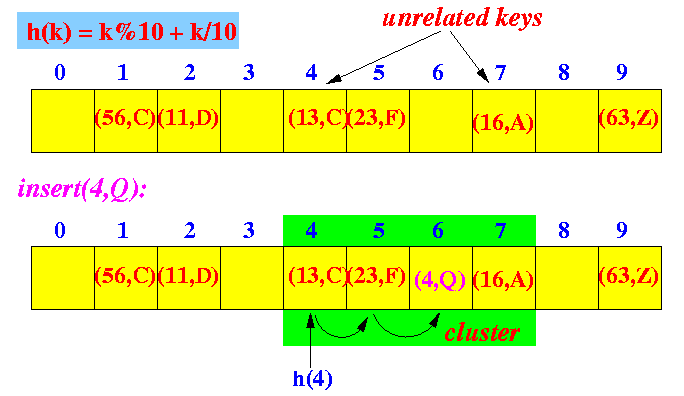
- Simple to implement
- Quadratic probing:
- More complex
- Can avoid the
clustering problem
created by linear probing
- However, the method can create a
different kind of clustering
called
secondary clustering
Example:
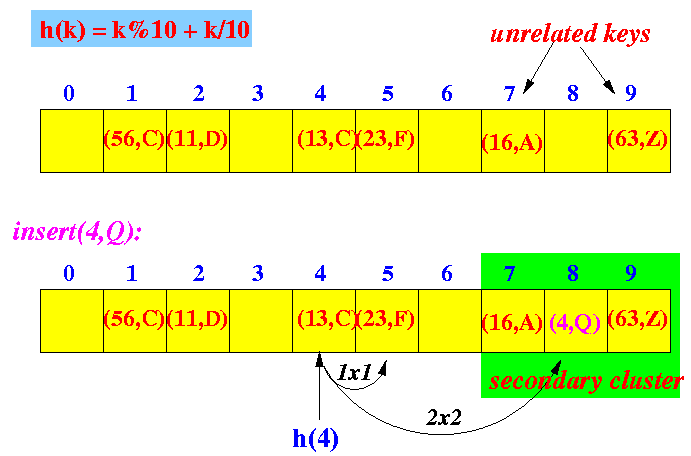
- More complex
- Linear probing: