Insert operations on AVL trees

Inserting a new entry into a binary search tree
- Example binary search tree:
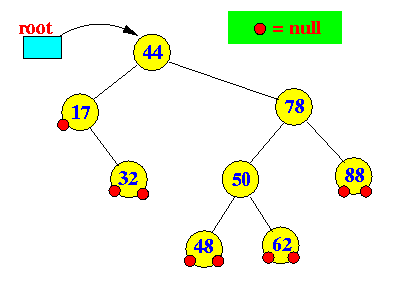
- Example: insert entry 46:
- Note:
Insertion in an AVL tree can lead to imbalance
- Sample AVL tree:
- Inserting an entry (node) can cause an AVL tree to become height imbalanced:
  (The resulting tree is no longer an AVL tree !!)

The precise effect of inserting a new node into an AVL tree

The two effects of inserting a node in an AVL tree:

Effect 1:
Example:
Therefore:

Effect 2:

If there are some nodes that have become height imbalanced, then the difference between the heights of the left and right trees is exactly = 2
Also: the larger value of the height is found in the nodes on the path from the newly inserted node to the root

Example:

(Because before the insertion, the difference between the heights was ≤ 1.

The insertion increased the height of one of the sub tree by ONE.

The difference between the heights is ≤ 2)

Re-balancing an AVL tree

Re-balance:

Re-balance = re-organize the nodes in an out-of-balanced AVL tree so that the resulting tree will satisfy the height constraint of an AVL tree
(I.e., the result of the re-balance operation is an AVL tree

Example:

AVL tree before inserting node 78:
AVL tree after inserting node 78:
The AVL tree is now out-of-balance because there are nodes in the tree with (height(left tree) - height(right tree)) = 2 :

We can re-arrange the shaded subtree as follows:

Before re-arranging nodes in shaded subtree	After re-arranging nodes in shaded subtree

Notice that:

The node re-arrangement must preserve the properties of a Binary Search Tree:
After the node re-arrangement, the resulting tree is an AVL tree !!!!

In what follows, I will explain the "node re-arrangement" operation that can re-balance an out-of-balance AVL tree
This "node re-arrangement" operation is called tri-node reconstruction operation (by Goodrich).
(BTW, the classic way to do re-balancing is with a bunch of "left-rotation", "right-rotation", "right-left-rotation", "right-right-rotation", etc..)

Re-arranging/re-balancing a binary tree: The tri-node restructuring operation

Consider the following sub tree of a binary tree:
From their relative positions of the nodes x, y and z , and the subtrees T₀, T₁, T₂ and T₃ in the AVL (binary) tree, we can conclude that:
In the node re-arrangement operation, we will always make a tree that look like this:
To preserve the property of a Binary Search Tree (left subtree with smaller keys and right subtree with larger keys), we must attach the subtrees T₀, T₁, T₂ and T₃ to the nodes x, y and z as follows:
This is the first tri-node reconstruction operation:

Note:

There are 4 different tri-node reconstruction operation (depending on the relative positions of the nodes x, y and z)
Here are the 4 different relative positions of the nodes x, y and z:

Teaching note:

Each configuration has its own tri-node reconstration operation

I have listed all 4 tri-node reconstration operations below if you want to take look at them: click here
I don't want to present the details of all 4 tri-node reconstration operations (because they are similar and you will hear the same story 4 times --- some of you will bored to death...)

So I will discuss the details of the first tri-node reconstration operation only

Rebalancing an AVL Tree - in general (for all 4 configurations)

How to use a tri-node reconfiguration operation to re-balance an AVL tree:

If after an insertion, the AVL tree is still balanced:

If after an insertion, the AVL tree becomes imbalanced:

Find the first imbalanced node from the point of insertion
(Recall that only node from inserted node ⇒ root can become imbalanced):
Apply the (appropriate for that configuration)) tri-node reconstruction operation on the tree rooted at the first imbalanced node = x:
The resulting tree will become balanced (i.e., an AVL tree !!!)

A concrete example:

After inserting node 46, the AVL tree becomes imbalanced:
Starting at the inserted node (46), traverse up the tree and find the first imbalanced node:
The AVL tree will become balanced again after we performed the (approriate) tri-node restructuring operation:

Procedure summary:

I did the example using configuration 1
The other configurations are similar

Precedure for re-balancing an AVL tree after insertion

Starting at the inserted node, traverse up the tree to find the first node
If not found, then done
Otherwsie: apply the (appropriate) tri-node restructuring operation using x as the first imbalanced node

$64,000 question:

Will this procedure guarantee that the resulting tree is an AVL tree ???
(If you can believe that without proof, I have a bridge in Brooklyn for sale :-))

Proposition: the tri-node restructuring operation will repair an imbalanced subtree due to insertion

Proposition:

Proof:

Suppose the AVL tree becomes imbalanced after we inserted a node w:
Since the node x is the first imbalanced node, its height must have increased by 1 !!!
The increase in height of node x can only be caused by a height increase in node y (and in node z)
Let's figure out what are the value of all the ? in the figure are first.
Because the tree was balanced before the insertion of w, we have that:
The height of T₁ can only be h−1 or h because the difference in height (with subtree T₀) is at most 1
(BTW, height of T₁ cannot be h+1, because otherwise node z will have height = h+2 !!!)
Then because node x is the first imbalanced node, we can conclude that:
The height of T₁ must be equal to h (otherwies, node z will be an earlier imbalanced node)
The height of T₂ must be equal to h+1 (otherwies, node y will be an earlier imbalanced node)
The height of T₃ must be equal to h+1 (otherwies, node x will be an balanced node)
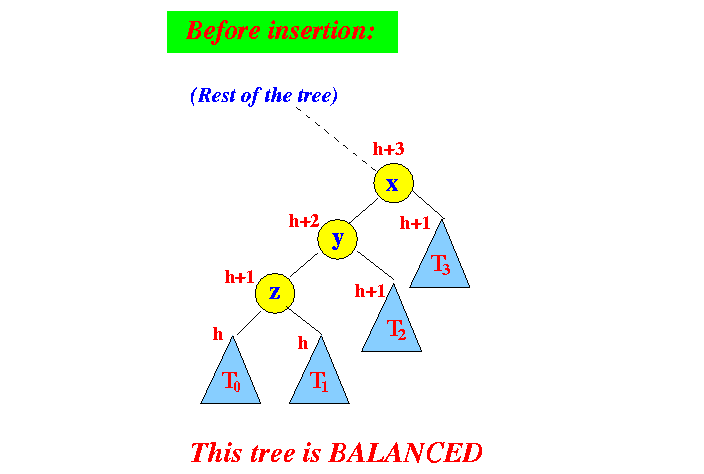
We now know the exact height before the insert operation:
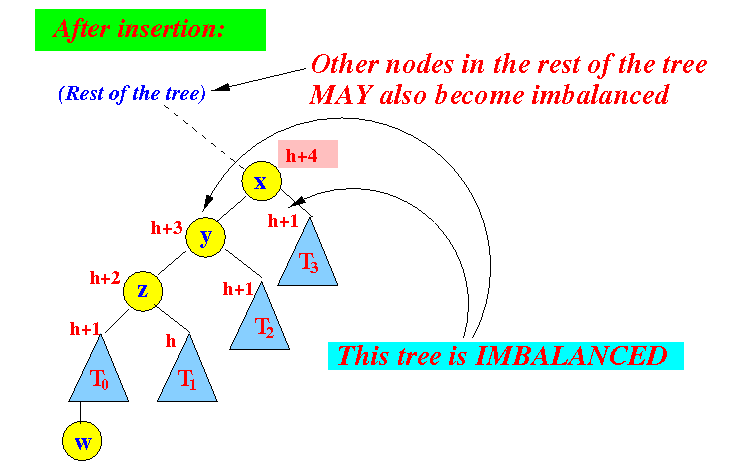
After the insert operation, the tree is:
After the tri-node reconstruction operation, the tree is:
We can see the tri-node reconstruction operation has fixed the height violation in node x
Question that remains:
Answer: yes because the height of the root node of the subtree after the tri-node reconstruction operation is the same as the original tree !!!
See:
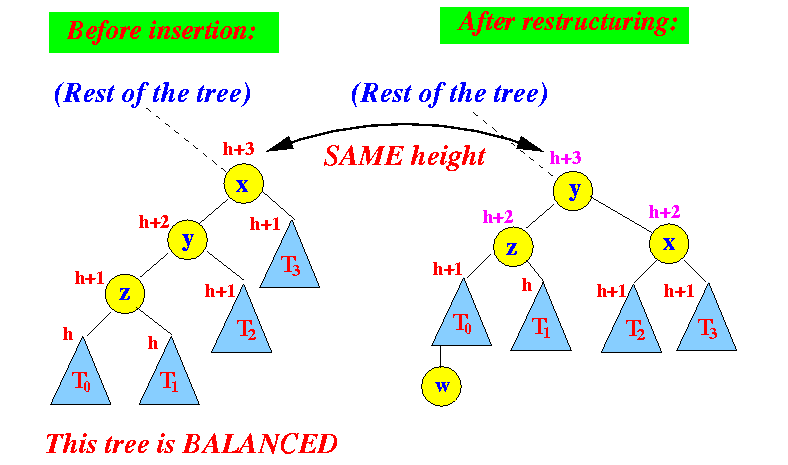
Since the rest of the tree was balanced when the subtree had height = h+3, therefore, the rest of the tree will be balanced because the subtree still has height = h+3 !!!

Conclusion:

The entire tree is re-balanced after the tri-node reconstruction operation !!!

The different (all possible) ways that an AVL tree can become height inbalanced

Notations:

w = the newly inserted node in the AVL tree
x = the first node in the (previously) AVL tree on the path from w to the root that is imbalanced
y = the child node of x in the (previously) AVL tree on the path from w to the root
z = the child node of y in the (previously) AVL tree on the path from w to the root

Graphically:

There are 4 possible parent/child relations between the nodes x, y and z:

The configurations can be characterized as follows:

Left-left configuration: y is left child of x and z is left child of y
Left-right configuration: y is left child of x and z is right child of y
Right-left configuration: y is right child of x and z is right child of y
Right-right configuration: y is right child of x and z is left child of y

Remember that:

Node x is always the first imbalanced node from the inserted node to the root !!!

Examples:

The 4 kinds of tri-node restructuring operations

Fact:

For each kind of configuration, there is a corresponding tri-node operation that re-balance the height of an imbalanced AVL tree !!!
Recall the 4 kinds of configurations:

If you want to discover the 4 different tri-node reconstruction operations yourself, you can do so by applying the following property:
I have spare you the discovery.... here are the 4 different tri-node reconstruction operations

Notation:

Because a tri-node reconstruction operation will always make the one of the following 4 configuration (of 3 nodes):
it is useful (especially when we write the code) to fix the different node with labels.
Labelling scheme:
In other words (or picture):

The 4 tri-node reconstruction operations:

Configuration 1:

Correspondence of node: a = z b = y c = x

Remember that the reconstruction operation must produce a Binary Search Tree.
In other words, you must preserve the property that the left subtree contains smaller key values and the right subtree contains larger key values !!!

Configuration 2:
Correspondence of node: a = y b = z c = x
Configuration 3:
Correspondence of node: a = x b = y c = z
Configuration 4:
Correspondence of node: a = x b = z c = y

The tri-node restructuring Algorithm

Peusdo code:

Let x = first imbalanced node Let y = child node of imbalance node x (on the way to the inserted node) Let z = grand child of imbalance node x (on the way to the inserted node) (1) Identify the configuration; which node is a ? which node is b ? which node is c ? where is subtree T0 (= root of subtree T0) ? where is subtree T1 (= root of subtree T1) ? where is subtree T2 (= root of subtree T2) ? where is subtree T3 (= root of subtree T3) ? (2) Make the links according to the tri-node reconstruction operation (build from the top first) (2.a) Make b the root of the new subtree x's parent must now point to b ! (Be careful: if x is the root node, b will become the new root !) (2.b) Now make these links: b / \ Note: don't forget the PARENT links !!! a c (2.c) Then these links: b / \ a c / \ T0 T1 (2.d) And finally these links: b / \ a c / \ T2 T3 Recompute the heights of a, c, b and all nodes from b to root. Done.

Tri-node restructuring algorithm in Java (my own version):

(Goodrich's code is Chinese to me... took me a while to figure out what he was trying to do, ain't not way in hell I'm using it to teach.....)

/* ======================================================= tri_node_restructure(x, y, z): x = parent(y) y = parent(z) ======================================================= */ public void tri_node_restructure( BSTEntry x, BSTEntry y, BSTEntry z) { /* ******************************************************************* Determine the parent child relationships between (y,z) and (x,y)) ******************************************************************* */ /* ======================================================= Determine the node configuration: find out which nodes are in positions a, b and c given in the following legend: b / \ a c / \ / \ T0 T1 T2 T3 ======================================================= */ BSTEntry a, b, c; BSTEntry T0, T1, T2, T3; boolean zIsLeftChild = (z == y.left); boolean yIsLeftChild = (y == x.left); if (zIsLeftChild && yIsLeftChild) { /* Configuration 1 */ a = z; // x=c b = y; // / \ c = x; // y=b T3 T0 = a.left; // / \ T1 = a.right; // z=a T2 T2 = b.right; // / \ T3 = c.right; // T0 T1 } else if (!zIsLeftChild && yIsLeftChild) { /* Configuration 2 */ a = y; // x=c b = z; // / \ c = x; // y=a T3 T0 = a.left; // / \ T1 = b.left; // T0 z=b T2 = b.right; // / \ T3 = c.right; // T1 T2 } else if (zIsLeftChild && !yIsLeftChild) { /* Configuration 4 */ a = x; // x=a b = z; // / \ c = y; // T0 y=c T0 = a.left; // / \ T1 = b.left; // z=b T3 T2 = b.right; // / \ T3 = c.right; // T1 T2 } else { /* Configuration 3 */ a = x; // x=a b = y; // / \ c = z; // T0 y=b T0 = a.left; // / \ T1 = b.left; // T1 z=c T2 = c.left; // / \ T3 = c.right; // T2 T3 } /* ------------------------------------------------------------------ Old Tree: New tree: x's parent x's parent | | x b Put b at x's place ------------------------------------------------------------------ */ if ( x == root ) { /* If x is the root node, handle the replacement differently.... */ root = b; // Need to update root ! b.parent = null; } else { BSTEntry xParent; xParent = x.parent; // Find x's parent if ( x == xParent.left ) { /* Link b to the left branch of x's parent */ b.parent = xParent; xParent.left = b; } else { /* Link b to the right branch of x's parent */ b.parent = xParent; xParent.right = b; } } /* ====================================================== Now we can make the REST of the tree (from b down) b / \ a c / \ / \ T0 T1 T2 T3 ======================================================= */ /* ------------------ Make: b / \ a c ------------------ */ b.left = a; a.parent = b; b.right = c; c.parent = b; /* ------------------ Make: b / \ a c / \ T0 T1 ------------------ */ a.left = T0; if ( T0 != null ) T0.parent = a; a.right = T1; if ( T1 != null ) T1.parent = a; /* ------------------ Make: b / \ a c / \ T2 T3 ------------------ */ c.left = T2; if ( T2 != null ) T2.parent= c; c.right= T3; if ( T3 != null ) T3.parent= c; /* ====================================== Recompute the heights of the nodes ====================================== */ recompHeight(a); recompHeight(c); }

The insert method for the AVL tree

It is now very straightforward to write the put()/insert method for an AVL tree:

public void put(String k, Integer v) { insert (k,v) using the ordinary BST put(k,v) algorithm; (I leave the code out for brevity) /* -------------------------------------------- Recompute the height of all parent nodes... -------------------------------------------- */ recompHeight(p); /* -------------------------------------------------------- Check for height violation starting at insert location -------------------------------------------------------- */ BSTEntry x, y, z; x = y = z = q; // Start search at q (new node) while ( x != null ) // Traverse all the way up to the root node.... { if ( diffHeight(x.left, x.right) <= 1 ) { /* ============================================= No violation --> continue to the next level ============================================= */ z = y; // Go up the tree one level y = x; x = x.parent; } else { break; // Found the first violation } } if ( x != null ) { tri_node_restructure( x, y, z ); // Re-balance the AVL tree } }

Example program
- Example Program: (Demo above code)
  - The BSTEntry.java Prog file: click here
  - The AVL_BST.java Prog file: click here
  - The test program TestAVL.java Prog file: click here
  How to run the program:
- Output of TestAVL: