Denominions of the coins:

Problem:   find the smallest # coins to make change for K cents

Example: make change for 5c:

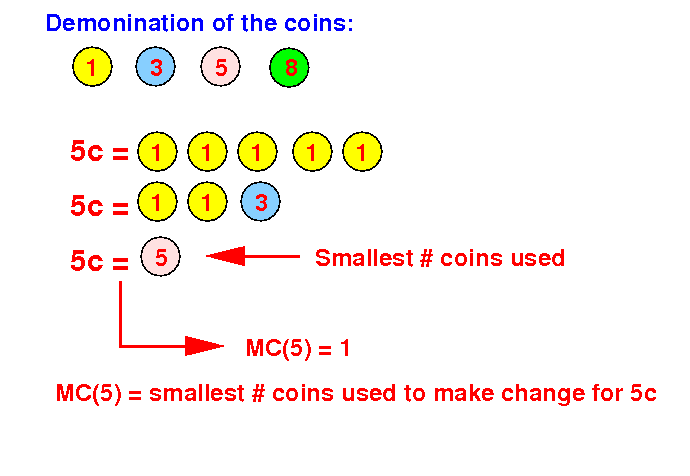
Solution:   MC(5) = 1 (coin)

Caveta:   the greedy method will not work:

Problem:   design an algorithm to find the smallest # coins to make change for the given values

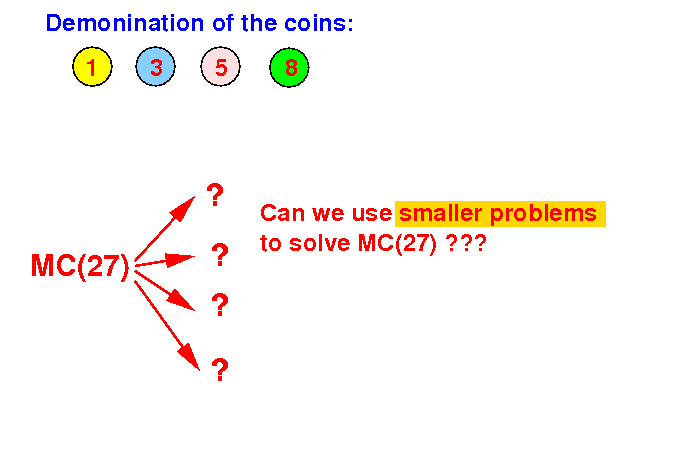
Problem description:   find smallest # coins to make change for 27c

Divide step:   find the smaller problems that are helpful

Hint:   we must use one of the 4 coins to make change !!!... Try all posibilties !!!

Divide step:   find the smaller problems that are helpful

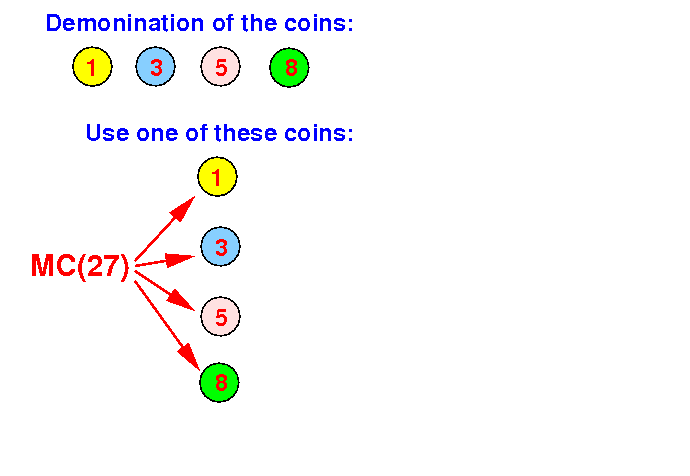
Question:   which smaller problems do we need to use ??

Divide step:   if we use coin with value 1, we need to make change for 27 − 1 = 26c:

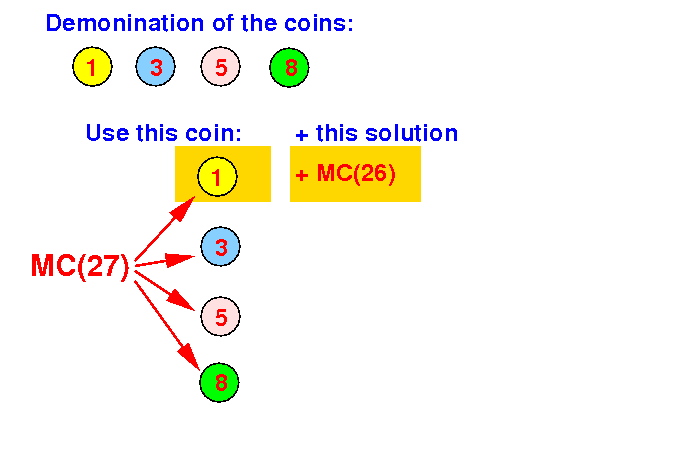
Question:   which smaller problems do we need to use ??

Divide step:   if we use coin with value 3, we need to make change for 27 − 3 = 24c:

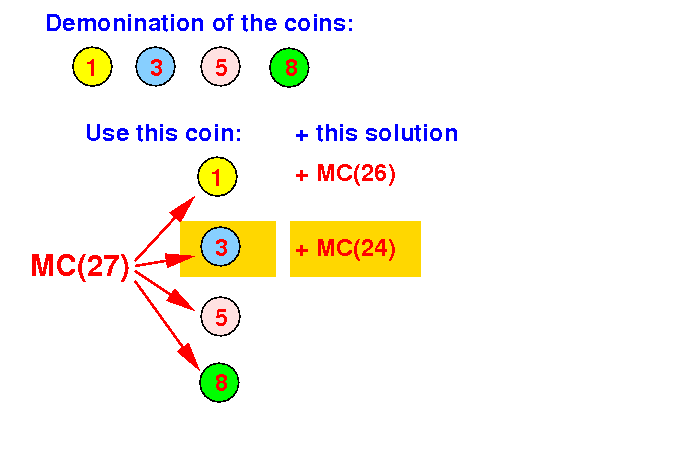
Question:   which smaller problems do we need to use ??

Divide step:   if we use coin with value 5, we need to make change for 27 − 5 = 22c:

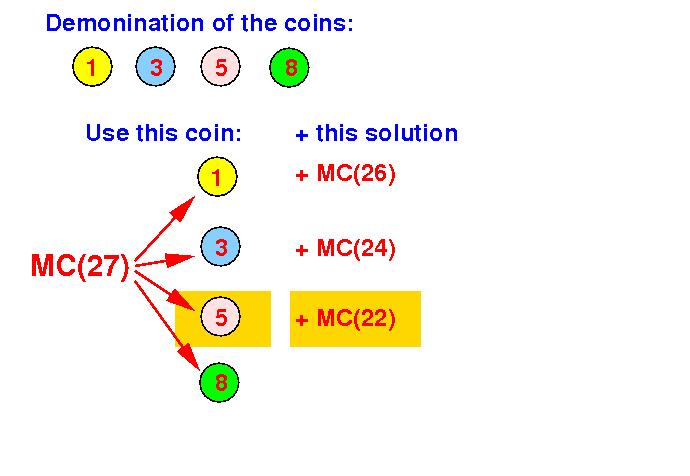
Question:   which smaller problems do we need to use ??

Divide step:   if we use coin with value 8, we need to make change for 27 − 8 = 19c:

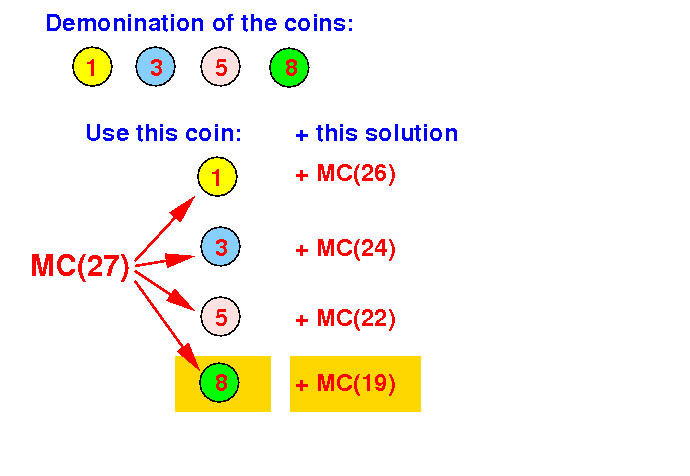
Question:   which smaller problems do we need to use ??

Divide step completed:   we have found the smaller problems that are helpful

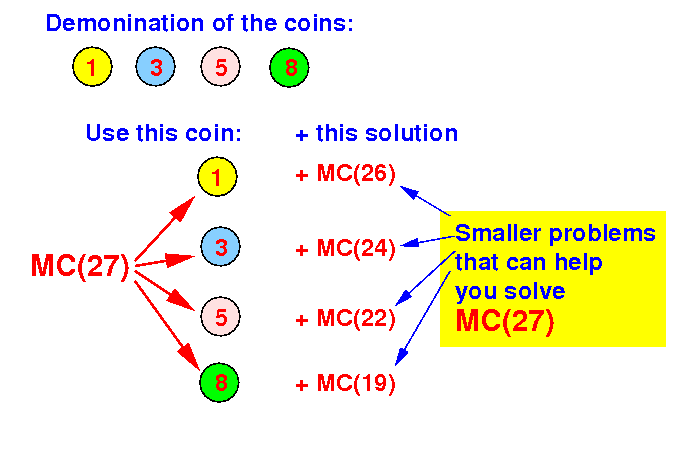
Conquer step:   how do we solve MC(27) if we are given the solutions for the smaller problems ?

Conquer:   suppose that you know these solutions:

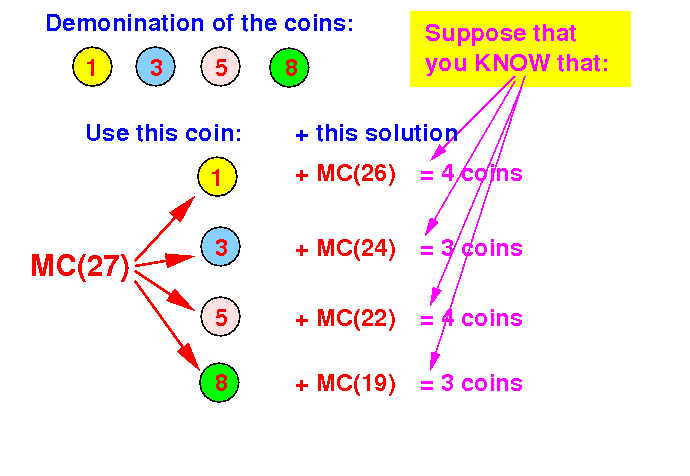
What is the smallest # coins used to make change for 27c ???

Conquer:   find the smallest number of coins that we need to use:

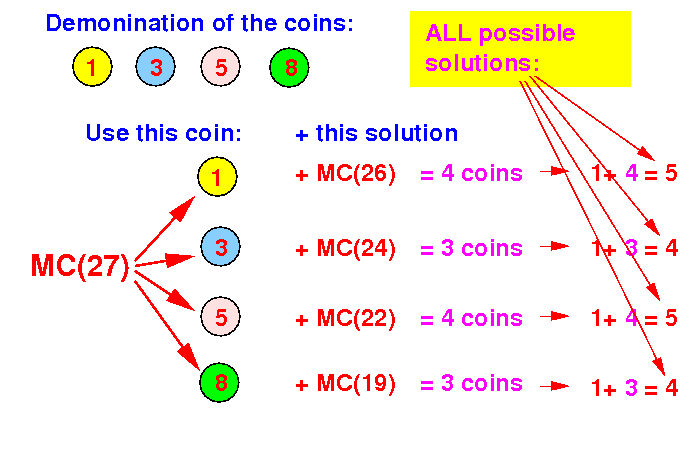
What is the smallest # coins used to make change for 27c ???

Divide and conquer:   use the solutions of the smaller problems

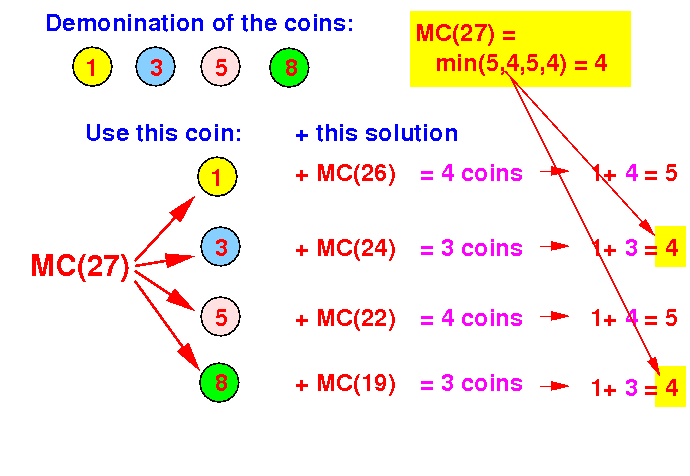
Answer:   MC(27) = 4 coins (3 + 1)

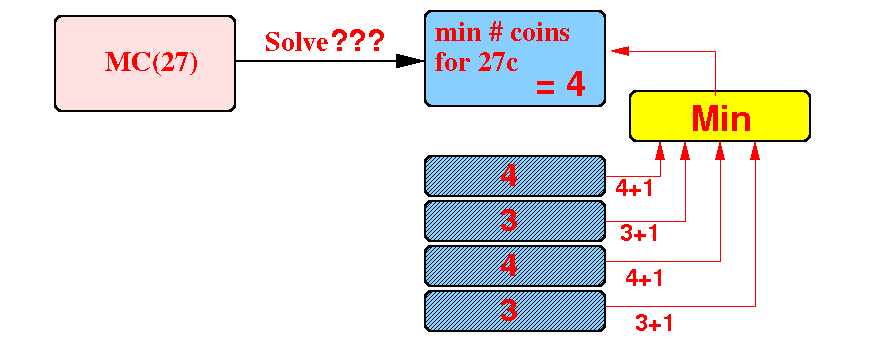
Suppose we need to solve the MC(27) problem:

Find the (useful) smaller problems to solve MC(27)

Use the solutions for the smaller problems to solve the original problem:

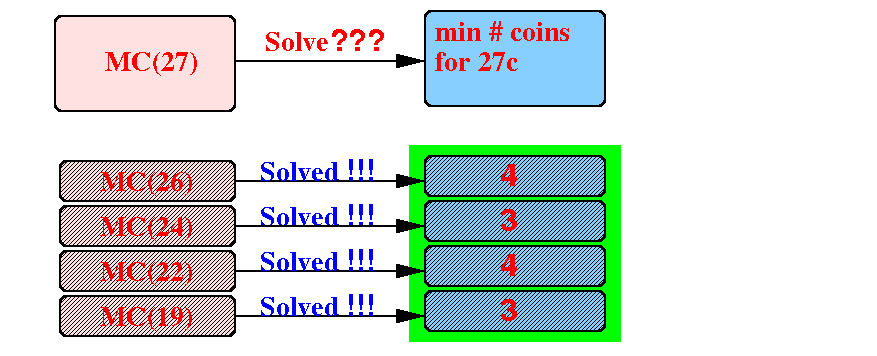
Note: we already have the solution, e.g., we know that MC(26) is equal to 4, etc !

We solve MC(27) using the values 4+1.3+1.4+1.3+1:

This is the essence of a recursive algorithm

def MC(amount):
    helpSol = [None,None,None,None] # These are my SOLVED problems

    # Base case: change for $0 uses no coins
    if (amount == 0):
        return 0

    # Find solutions for the smaller problems used to solve MC(amount)

    # 1st smaller problem when I use a coin with value 8
    # ** I can only use this coin if we make change for an amount >= 8 **
    if ( amount >= 8 ):
        helpSol[0] = MC(amount-8)      # DELEGATE !
                     # min num coins used to make change for amount-8

    # 2nd smaller problem when I use a coin with value 5
    # ** I can only use this coin if we make change for an amount >= 5 **
    if ( amount >= 5 ):
        helpSol[1] = MC(amount-5)      # DELEGATE !
                     # min num coins used to make change for amount-5

    # 3rd smaller problem when I use a coin with value 3
    # ** I can only use this coin if we make change for an amount >= 3 **
    if ( amount >= 3 ):
        helpSol[2] = MC(amount-3)      # DELEGATE !
                     # min num coins used to make change for amount-3

    # 4th smaller problem when I use a coin with value 1
    # ** I can only use this coin if we make change for an amount >= 1 **
    if ( amount >= 1 ):
        helpSol[3] = MC(amount-1)      # DELEGATE !
                     # min num coins used to make change for amount-1

    # Solve my problem USING the smaller solutions:
    mySol = min( x for x in helpSol if x != None) + 1 
    return mySol
   

DEMO:   C:\ClassUp\mc.py