- Matrix multiplication:
- Matrix multiplication = an operation on 2 matrices where you multiply the row vectors of the first matrix with the column vectors of the second matrix
- Example of
matrix multiplication:
Multiply two 3×3 matrices: +- -+ |A11 A12 A13| A = |A21 A22 A23| |A31 A32 A33| +- -+ +- -+ |B11 B12 B13| B = |B21 B22 B23| |B31 B32 B33| +- -+ Then: +- -+ |C11 C12 C13| C = A*B = |C21 C22 C23| |C31 C32 C33| +- -+ where: Cij = Ai1*B1j + Ai2*B2j + Ai3*B3j (for i = 1, 2, 3 and j = 1, 2, 3) or: +- -+ | B1j | Cij = ( Ai1 Ai2 Ai3 ) * | B2j | | B3j | +- -+
+- -+ +- -+ +- -+ | 2 3 1 | | 3 6 2 | | 2*3 + 3*2 + 1*1 2*6 + 3*2 + 1*1 ... | | 6 2 3 | * | 2 2 4 | = | 6*3 + 3*2 + 3*1 | | 4 7 1 | | 1 1 3 | | 4*3 + 7*2 + 1*1 | +- -+ +- -+ +- -+ +- -+ | 13 19 19 | = | 25 43 29 | | 27 39 39 | +- -+
- Mathematically expressed:
Cij = ∑k=0..N-1 AikBkj for i = 0, 1, 2, ..., N-1 j = 0, 1, 2, ..., N-1
- Matrix multiplication using
defined array variables
(we can define
a 2-dim array to store
a matrix):
int N = ...; // Some pre-defined value float A[N][N]; // Matrix 1 float B[N][N]; // Matrix 2 float C[N][N]; // Output matrix /* =============================================================== CPU matrix multiplication alg for static 2-dimensional arrays =============================================================== */ for (int i = 0; i < N; i++) for (int j = 0; j < N; j++) { /* --------------------------------- Compute the matrix element Cij = ∑k=0..N-1 AikBkj --------------------------------- */ C[i][j] = 0.0; for (int k = 0; k < N; k++) C[i][j] = C[i][j] + A[i][k]*B[k][j]; // Vector product }
- Example Program:
(Demo above code)

/home/cs355001/demo/CUDA/4-mult-matrix/cpu-mult-defined-matrix.c Compile: nvcc -g cpu-mult-defined-matrix.c -o cpu-mult-defined-matrix Run: cpu-mult-defined-matrix #rows Example: cs355@ghost01 (1886)> cpu-mult-defined-matrix 4 Elasped time = 1 micro secs Matrix A: 1.80 1.68 1.96 0.72 0.60 1.03 0.78 2.04 1.37 Matrix B: 0.85 1.71 0.42 1.65 1.19 1.35 1.10 1.97 1.54 Matrix C = A*B: 6.46 8.95 6.05 2.72 3.96 2.69 5.54 6.46 5.20Problem with defined arrays: limited size due to stack size:
cs355@ghost01 (2684)> cpu-mult-defined-matrix 1000 // Can't handle 1000x1000 matrix... Memory fault(coredump)
Solution:
- Allocate memory to store array using calloc( )/malloc( )
- Important fact:
- We can only dynamically allocate
one-dimensional arrays
- A matrix is a two-dimensional array !!
If we store a matrix using a dynamically allocated array:
- We must map the matrix elements onto the one-dimensional array !!!
- We can only dynamically allocate
one-dimensional arrays
- Mapping a
two-dimensional array
onto a
one-dimensional array:
- "Mapping" the
matrix elements:
- "Map the elements" = find a relationship of the indices of the matrix elements and the indices of the one-dimensional array
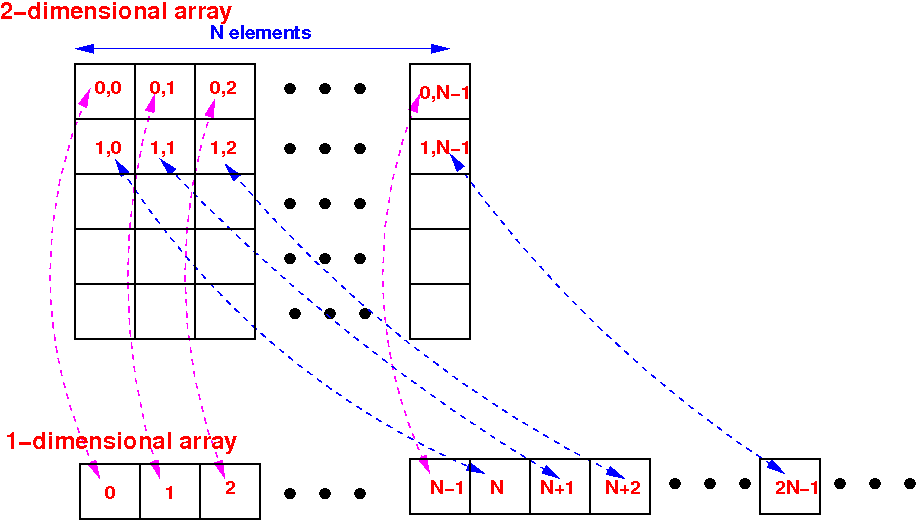
- The following diagram
shows a
mapping of
a two-dimensional array (matrix)
onto a
one-dimensional array:
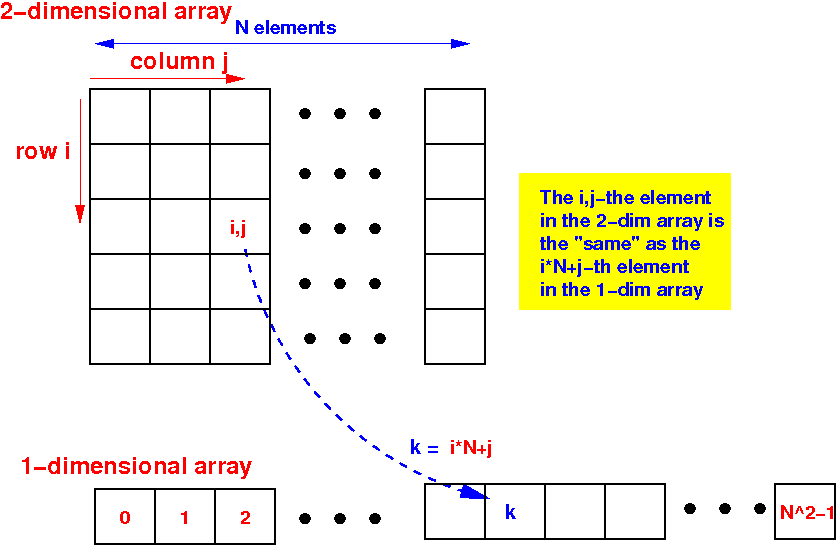
- The mapping function
for a 2-dimensional coordinate (i,j)
to a one-dimensional coordinate k is:
k = i×N + j
Graphically:
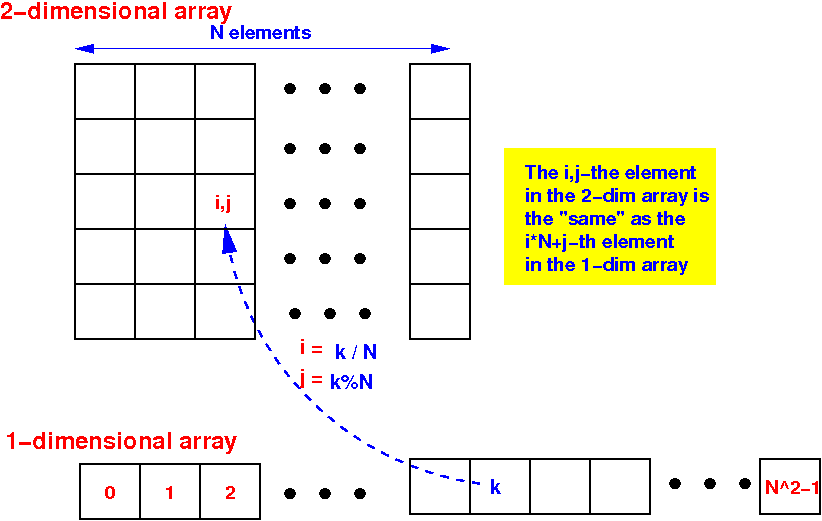
- The mapping function
for a 1-dimensional coordinate k
to a 2-dimensional coordinate (i,j) is:
i = k/N j = k%N
Graphically:
- "Mapping" the
matrix elements:
- How to allocate
dynamic array variables in
C:
float *A; A = calloc( N*N, sizeof(float) ); // Allocate an array of N*N elements of floats
How to use the allocated array:
A[0] = first element of array A[1] = second element of array A[i] = i-th element of the array
- Matrix multiplication using
dynamically allocated
array variables:
int N = ...; // Some pre-defined value float *A; // Dynamically allocated Matrix 1 float *B; // Dynamically allocated Matrix 2 float *C; // Dynamically allocated Output matrix /* ==================================== Allocate arrays ==================================== */ A = calloc(N*N, sizeof(float)); B = calloc(N*N, sizeof(float)); C = calloc(N*N, sizeof(float)); /* =============================================================== CPU matrix multiplication alg for dynamically allocated arrays =============================================================== */ for (int i = 0; i < N; i++) for (int j = 0; j < N; j++) { /* --------------------------------- Compute the matrix element Cij = ∑k=0..N-1 AikBkj --------------------------------- */ C[i*N+j] = 0.0; for (int k = 0; k < N; k++) C[i*N+j] = C[i*N+j] + A[i*N+k]*B[k*N+j]; // Vector product }
- Example Program:
(Demo above code)

/home/cs355001/demo/CUDA/4-mult-matrix/cpu-mult-matrix.c Compile: nvcc -g cpu-mult-matrix.c -o cpu-mult-matrix Run: cpu-mult-matrix #rows Example: cs355@ghost01 (1886)> cpu-mult-matrix 4 Elasped time = 1 micro secs Matrix A: 1.80 1.68 1.96 0.72 0.60 1.03 0.78 2.04 1.37 Matrix B: 0.85 1.71 0.42 1.65 1.19 1.35 1.10 1.97 1.54 Matrix C = A*B: 6.46 8.95 6.05 2.72 3.96 2.69 5.54 6.46 5.20 Stress test: cs355@ghost01 (1938)> cpu-mult-matrix 1000 Elasped time = 6570789 micro secs
- Thread organization and
workload for
each thread:
- We multiply a
N×N matrix
using N2 threads
- The workload for
the thread k is:
- Thread k will
compute the
matrix element Cij where:
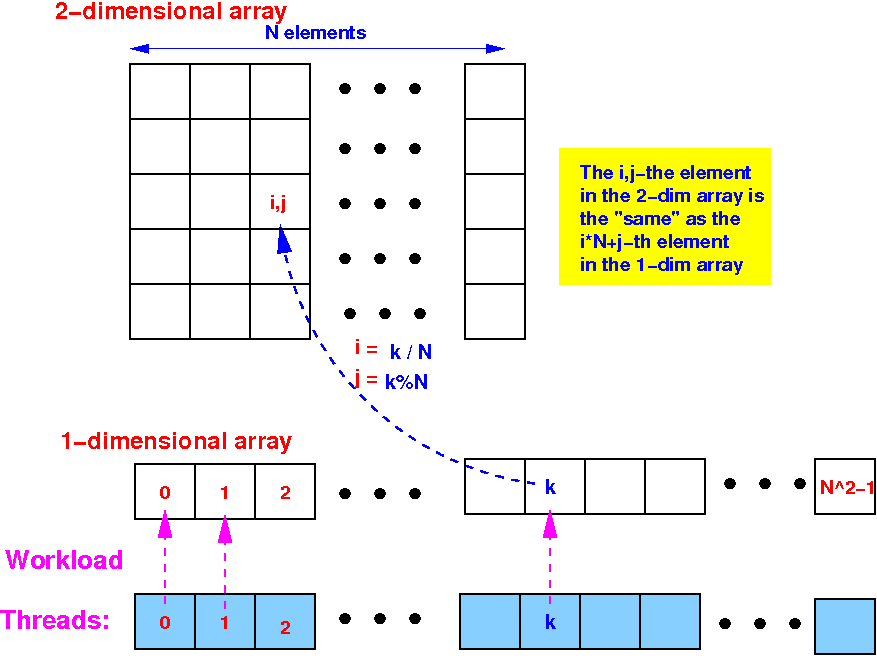
How to compute Cij:
Thread k computes Cij as follows: Cij = ∑k=0..N-1 AikBkj - Thread k will
compute the
matrix element Cij where:
- We multiply a
N×N matrix
using N2 threads
- GPU program for
matrix multiplication:
/* ================================================================== Kernel function to compute C[w] = C[i][j] where i = w/N, j = w%N Algorithm to compute C[i][j]: C[i][j] = sum_{k=0..n} A[i][k]*B[i][k] ================================================================== */ __global__ void matrixMult(int n, float *C, float *A, float *B) { int w = blockIdx.x*blockDim.x + threadIdx.x; // Unique thread ID if ( w < n*n ) { int row = w/n; // Row index int col = w%n; // Column index C[row*n+col] = 0.0; // We could also use: C[w] = 0.0 for ( int k = 0; k < n; k++ ) C[row*n+col] += A[row*n+k] * B[k*n+col]; // C[row*n+col] = C[w] // Computes: Cij = ∑k=0..N-1 AikBkj (row = i, col = j) } }
// We launch N*N threads in main( ) int main(int argc, char *argv[]) { ... initialization code omitted for brevity ... int K = 256; // My preferred K int NBlks = ceil((float) N*N / K ); // ================================================================== // Run kernel on the GPU using NBlks block, K thread/per block matrixMult<<<NBlks, K>>>(N, C, A, B); // Wait for GPU to finish before accessing on host cudaDeviceSynchronize(); // ==================================================================
- Example Program:
(Demo above code)

Program: /home/cs355001/demo/CUDA/4-mult-matrix/mult-matrix.cu Compile: nvcc -o mult-matrix.o -c mult-matrix.cu Sample: cs355@ghost01 (1939)> mult-matrix 1000 K = 256 N*N = 1000000/K = 256 = 3906.250000 ---> use 3907 blocks Elasped time = 43152 micro secs #errors = 0