Slideshow:
- Fact2:
- Because
all objects in
the subtree indexed by
its bounding box is
completely contained inside
the bounding box,
we can use the dimension of the
bounding box to
decide whether we
need to search the
subtree.
- Because bounding boxes can
overlap,
we may
need to
search in multiple subtrees
to find
the object
- The search algorithm in
an R-tree is
based on the depth-first search
tree traversal algorithm
- A branch of the R-tree will be search only if the object that you want to find is located within the corresponding bounding box (= search key !!!)
- Because
all objects in
the subtree indexed by
its bounding box is
completely contained inside
the bounding box,
we can use the dimension of the
bounding box to
decide whether we
need to search the
subtree.
- Searching problem
for a Point(x,y):
- Given a point (x,y)
- Find the object(s) in the R-tree that contains the point (x,y)
- Given a point (x,y)
- Search algorithm for
objects containing
a Point P(x,y) when the
current node is
n:
(initially n = root)
/* ==================================================================== Lookup( (x,y), n, result ): Look for object that contain point (x,y) (x,y) = coordinate of a point n = current node of search result = output Comment: it's a DFS algorithm with pruning on (x,y) ∉ Subtree ==================================================================== */ Lookup( (x, y), n, result ) { // n = current node of the search in the R-tree if ( n == internal node ) { for ( each entry ( BB, childptr ) in internal node n ) do { /* =============================================== Look in subtree if (x,y) is inside bounding box =============================================== */ if ( (x,y) ∈ BB ) { Lookup( (x,y), childptr, result); } } } else { /* ======================================= n is a leaf node.... ======================================= */ for ( each object Ob in node n ) do { if ( (x,y) ∈ MBB(Ob) ) { Add Ob to result; // Object Ob contains point (x,y) } } }
- Example 1:
Find the object(s) that contain
the point P(40,75):
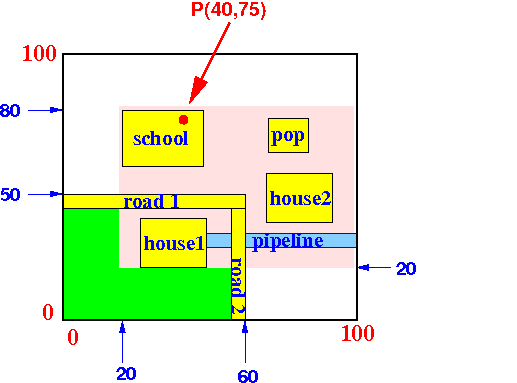
Execution of the search algorithm:
- Input:
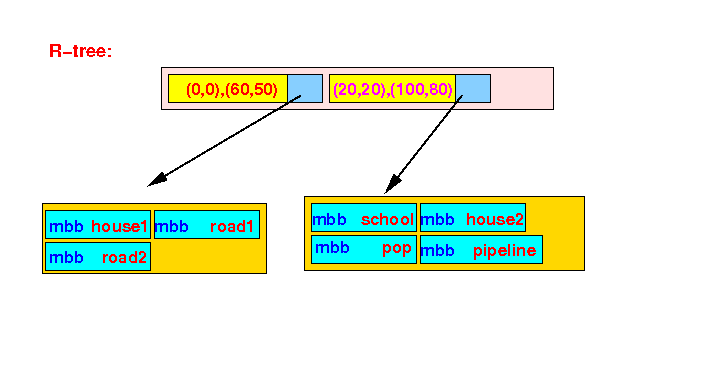
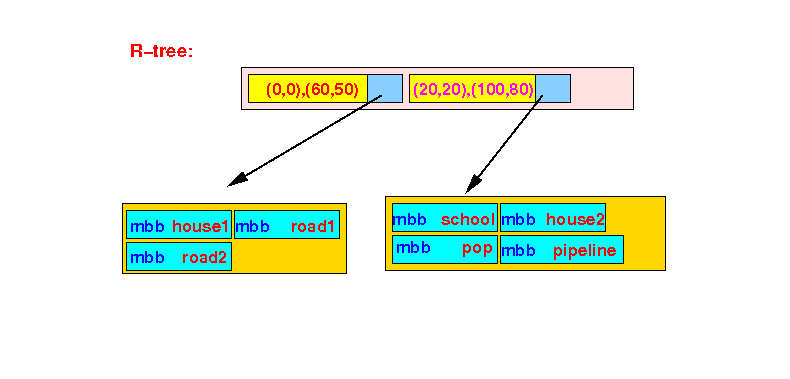
- R-tree:
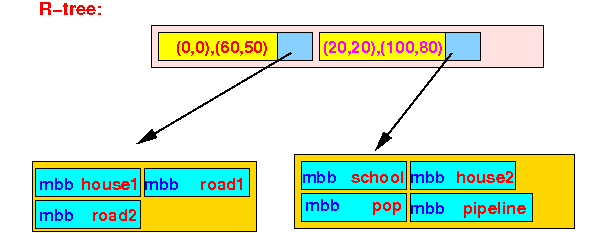
- Point (40,70)
- R-tree:
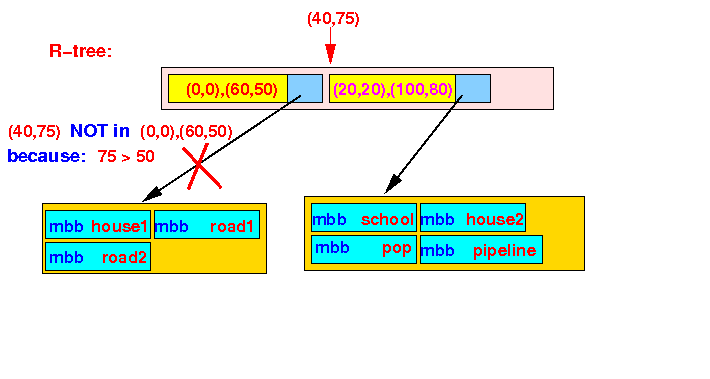
- Check in
first Bounding Box:
- point P(40,75) ∉ bounding box ((0,0),(60,50))
We skip the first subtree:
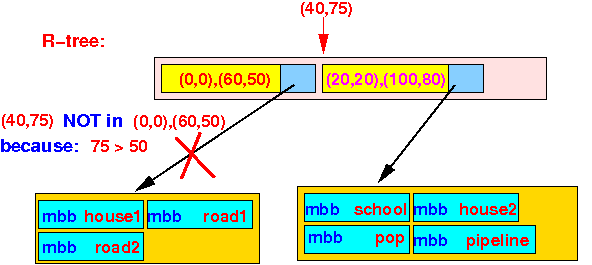
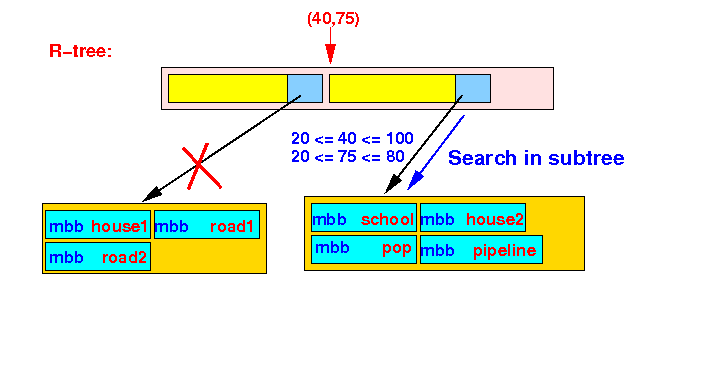
- Check in
second Bounding Box:
- point P(40,75) ∈ bounding box ((20,20),(100,80))
The search algorithm will recurse and search the 2nd subtree:
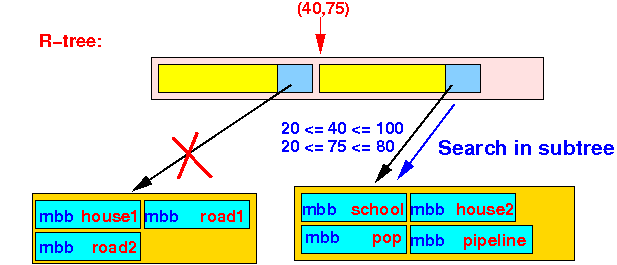
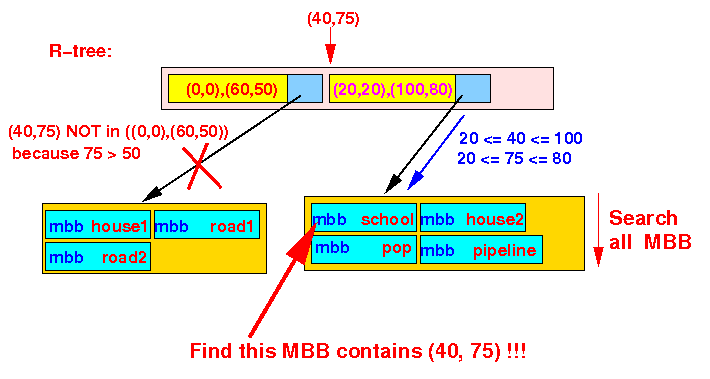
- We arrived at a
leaf node,
so we search the
MBBs (Min. Bounding Box) in
the leaf node:
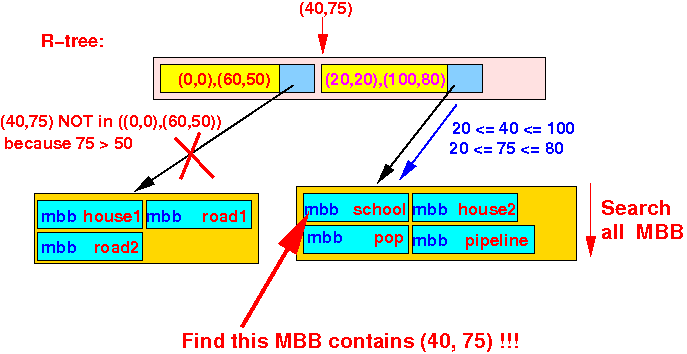
We find that the school object contain the point
- Input:
- Example 2:
Find the object(s) that contain
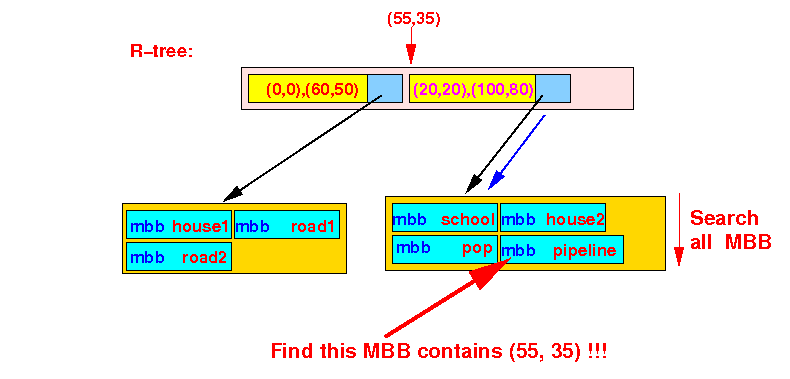
the point P(55,35):
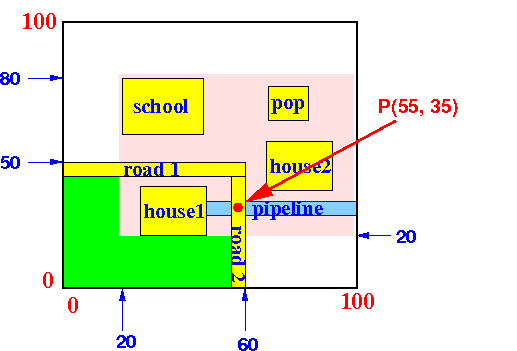
Execution of the search algorithm:
- Input:
- R-tree:

- Point (55,35)
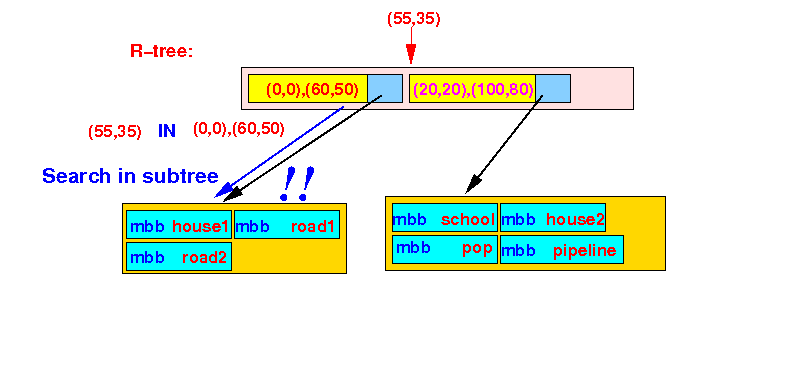
- R-tree:
- Check in
first Bounding Box:
- point P(55,35) ∈ bounding box ((0,0),(60,50))
The search algorithm will recurse and search the 1st subtree:
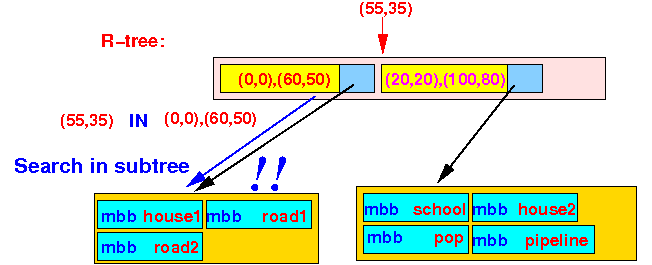
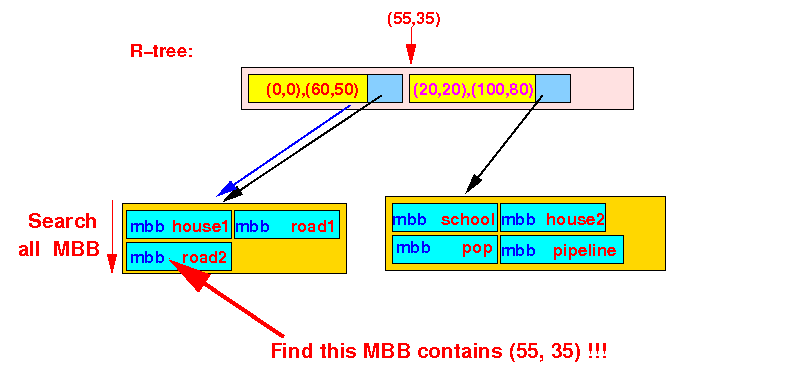
- We arrived at a
leaf node,
so we search the
MBBs (Min. Bounding Box) in
the leaf node:
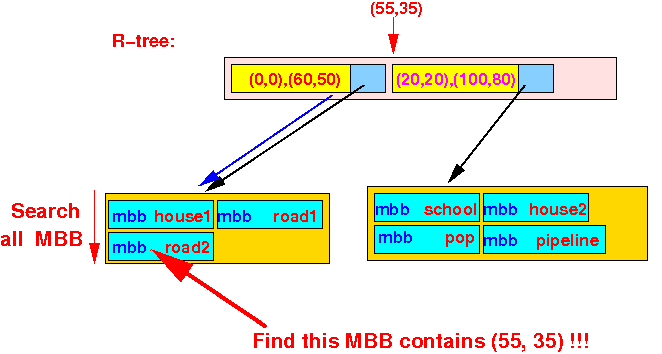
We find that the road2 object contain the point
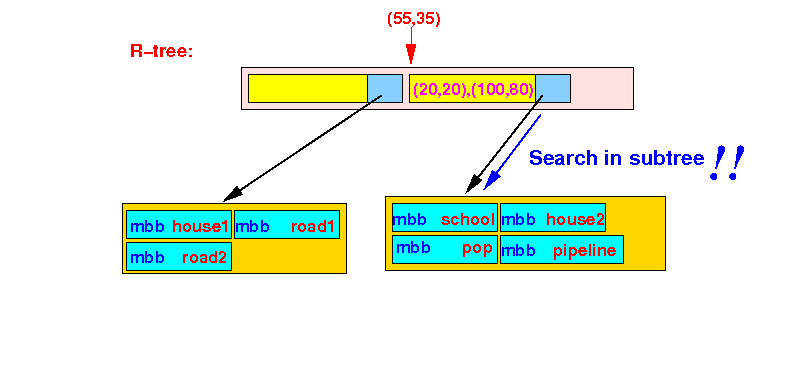
- Check in
second Bounding Box:
- point P(55,35) ∈ bounding box ((20,20),(100,80))
The search algorithm will also recurse and search the 2nd subtree:
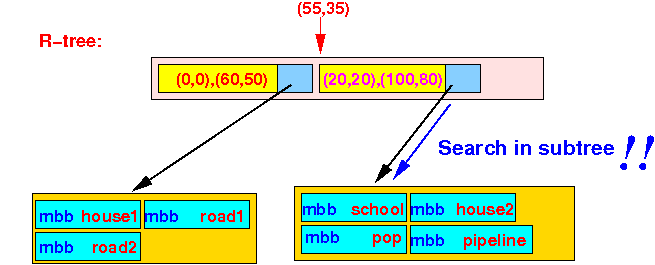
- We arrived at a
leaf node,
so we search the
MBBs (Min. Bounding Box) in
the leaf node:
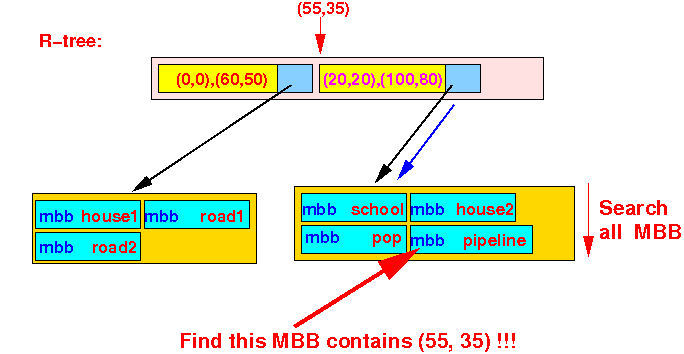
We find that the pipeline object contain the point
- Input:
- Simplification:
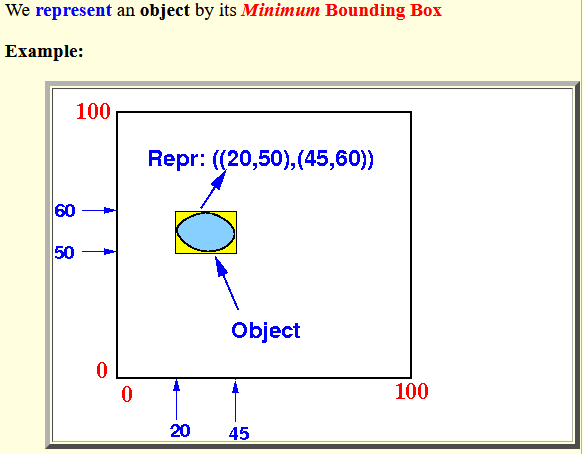
- We represent an
object by its
Minimum Bounding Box
Example:
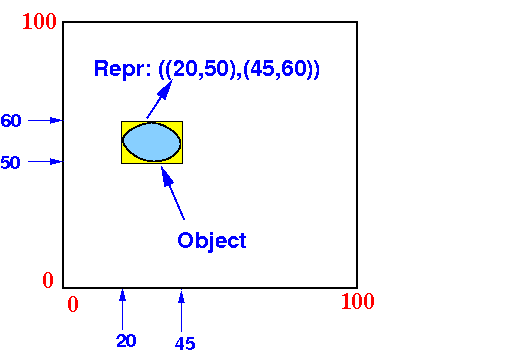
- We represent an
object by its
Minimum Bounding Box
- Containment relationship of
bounding boxes:
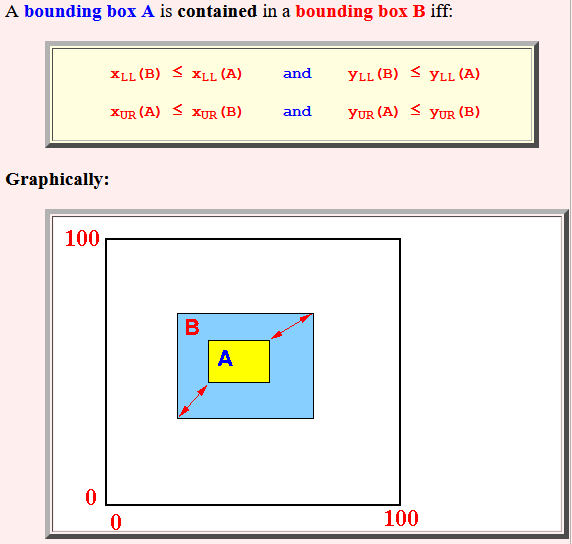
- A bounding box A is
contained in a
bounding box B iff:
xLL(B) ≤ xLL(A) and yLL(B) ≤ yLL(A) xUR(A) ≤ xUR(B) and yUR(A) ≤ yUR(B)Graphically:
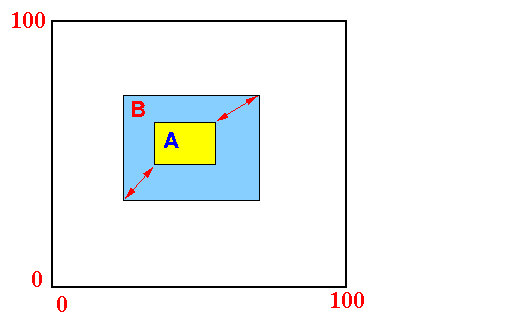
- A bounding box A is
contained in a
bounding box B iff:
- Search algorithm for
objects in an
R-tree:
- Is similar to the search algorithm for points using the containment relationship for bounding boxes.
Algorithm to find rectangle Obj
/* ==================================================================== Lookup( Obj, n, result ): Look for object that contain rectangle Obj Obj = representation of a rectangle object n = current node of search result = output ==================================================================== */ Lookup( Obj, n, result ) { // n = current node of the search in the R-tree if ( n == internal node ) { for ( each entry ( BB, childptr ) in internal node n ) do { /* =============================================== Look in subtree if Obj is inside bounding box =============================================== */ if ( Obj ⊆ BB ) { Lookup( Obj, childptr, result); } } } else { /* ======================================= n is a leaf node.... ======================================= */ for ( each object Ob in node n ) do { if ( MBB(Obj) == MBB(Ob) ) { Add Ob to result; // Object Ob contains point Obj return; // Obj found, done !! } } }