Slideshow:
Overflow condition
Causing an overflow condition...
How should be re-distribute the
indexes (= bounding boxes)
over 2 nodes ?
Because a smaller bounding box provides more accurate search "region"
How should be re-distribute the
indexes (= bounding boxes)
over 2 nodes ? -
criteria
How should be re-distribute the
indexes (= bounding boxes)
over 2 nodes ? -
criteria
Problem description:
A naive/brute force node partitioning algorithm
for the R-tree
Algorithm: try every possible combination of splits
Example: split this set of bounding boxes (= indexes) into 2 sets with smallest total area
A naive/brute force node partitioning algorithm
for the R-tree
Algorithm: try every possible combination of splits
Possible split #1:
A naive/brute force node partitioning algorithm
for the R-tree
Algorithm: try every possible combination of splits
Possible split #2:
A naive/brute force node partitioning algorithm
for the R-tree
Algorithm: try every possible combination of splits
Possible split #3:
A naive/brute force node partitioning algorithm
for the R-tree
Algorithm: try every possible combination of splits
Possible split #4: (and so on...)
A naive/brute force node partitioning algorithm
for the R-tree
Algorithm will find the best partition, but it has running time O(2n) (number of subsets is exponential) !
A (O(n2)) node partitioning algorithm
for the R-tree
Algorithm has
running time
O(n2)...
BUT:
it is
not guaranteed to
find the best (least area) partition
(The R-tree paper (see below in webpage) describes another algorithm that is O(n))
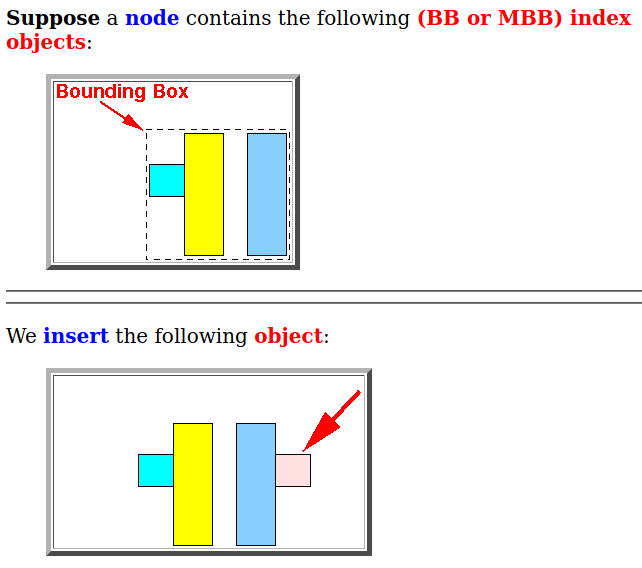
- Suppose a node
contains the
following (BB or MBB) index objects:
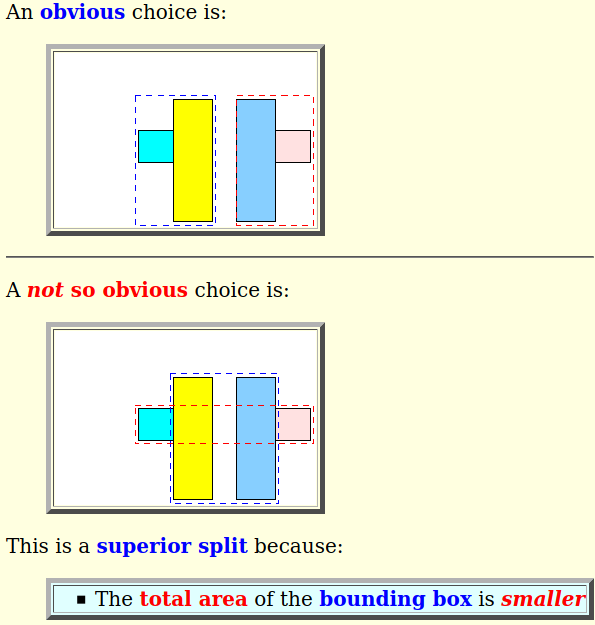
- We insert the following
object:
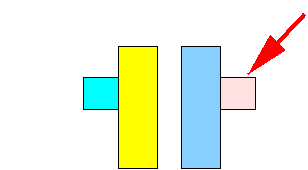
- The node is now
overflow and we
want to
split the
objects into
2 groups.
How should the objects be split ????
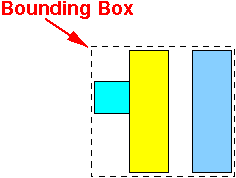
- An obvious choice is:
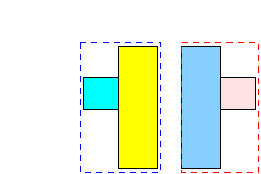
- A not so obvious choice is:
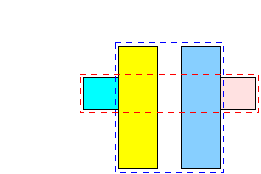
This is a superior split because:
- The total area of the bounding box is smaller
- An obvious choice is:
- Fact:
- The smaller a Bounding Box, the more precisely the Bounding Box describes a search area
Therefore:
- When we split the
(search) Bounding Boxes in
a node:
- We want to minimize the total area of the bounding boxes of the split
- Problem description:
- Given a set of n
objects
- Find the partitioning
of the n
objects
into
2 groups A and B such that:
AreaOfMBB(objects in A) + AreaOfMBB(objects in B) = minimal
- Given a set of n
objects
- Naive Algorithm:
S = all possible subsets of {1 , 2, 3,...., n}; Initialize minArea: s1 ∈ S; // Pick the first subset in S best_A = s1 best_B = {1,2,3,...,n} - s; // Completement set minArea = AreaOfBB(objects in A) + AreaOfBB(objects in B); /* ================================================= Brute force: test every possible split... ================================================= */ for ( each subset s ∈ S - s1 ) do { A = s; B = {1,2,3,...,n} - s; Area = AreaOfBB(objects in A) + AreaOfBB(objects in B); if ( Area < minArea ) { minArea = Area; // New best !!! best_A = A; best_B = B; } }
- Example:
- Split the following
Bounding boxes:
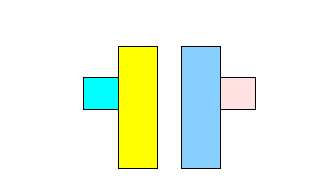
- Brute force consider
all the following
split cases:
-
1.
-
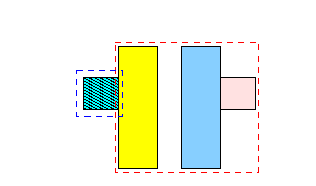
2.
-
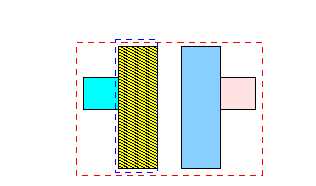
3.
-
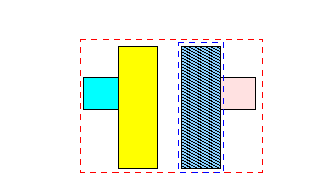
4.
-
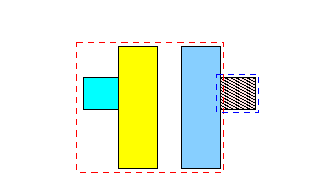
5.
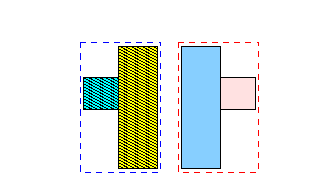
6.
And so on....
Running time of the naive (brute-force) algorithm:
Complexity of the naive re-distribute alg = O(2n-1) (# subsets of a set of n elements = 2n) (We need to consider half of all subsets due to symmetry) - Split the following
Bounding boxes:
- There exists a
O(n2)
algorithm
to find the
reasonably good partitioning
Abstractly:
1. Pick 2 "seed" objects e1 and e2 that are "as far apart" from each other as possible Group1 = { e1 }; Group2 = { e2 }; 2. while ( remaining elements ≠ ∅ ) { nextElem1 = the un-inserted element that will increase the BB of Group1 by the least amount nextElem2 = the un-inserted element that will increase the BB of Group2 by the least amount if ( increase in BB when adding nextElem1 to Group1 < increase in BB when adding nextElem1 to Group2 ) { Add nextElem1 to Group1; } else { Add nextElem2 to Group2; } }This O(n2) algorithm is described in this reference paper: click here