- Important fact:
- The join (⋈) operation is an essential operation in query processing
Therefore, it is very important that:
- The join (⋈) operation
have a
flexible
(= wide variety) of
implementation algorithms
varying from:
-
Very efficient:
with low disk I/O cost
but
high memory requirement)
E.g.: the one-pass join (⋈) algorithm --- click here
- Extremely low memory requirement but high disk I/O cost
-
Very efficient:
with low disk I/O cost
but
high memory requirement)
- Nested-loop
Join algorithm:
- Nested-loop Join =
a "family" of
algorithms for the
join operator
that can be used
for relations of
any size
(i.e.: algorithm uses very little memory buffers)
- Nested-loop Join =
a "family" of
algorithms for the
join operator
that can be used
for relations of
any size
- Algorithm for
R(X,Y) ⋈ S(Y,Z):
for ( each tuple s ∈ S ) do { for ( each tuple r ∈ R ) do { if ( r(Y) == s(Y) ) { output (r, s); } } }
Worst case performance:
# Disk I/O = T(S) × T(R)Advantage:
- Requires only
2 input buffers
(1 buffer to read tuples for relation S and 1 buffer to read tuples for relation R)
- Requires only
2 input buffers
- Note:
- The tuple-based nested-loop join can be implemented as an iterator
- Iterator for
the R ⋈ S
operation:
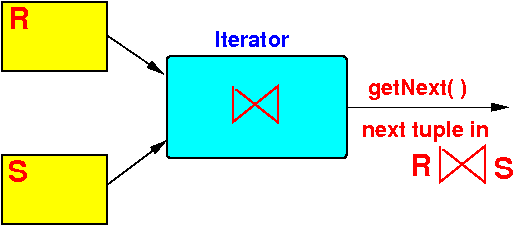
- Implementation of
Open( ):
Open( ) { R.Open( ); S.Open( ); s = S.getNext(); // s = current tuple of S }Graphically:
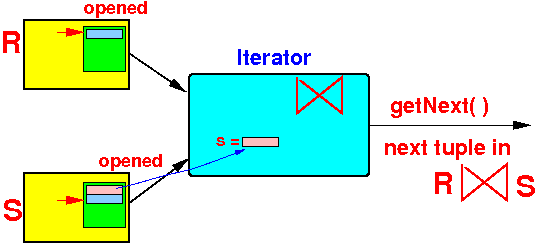
- Implementation of
getNext():
Note:
- getNext( ) will
output the
next tuple in
R ⋈ S
I.e.:
- Initially:
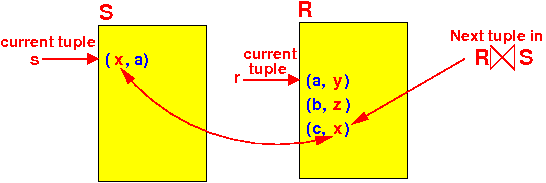
- getNext( ) will
return
the tuple
(x, a, c,
x)
New state of the iterator:
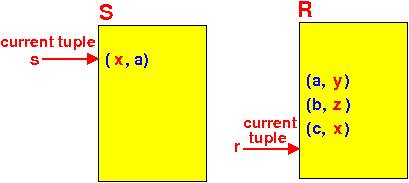
- Initially:
getNext( ) algorithm in pseudo code:
/* ------------------------------------------------------------------ getNext( ): output the next (just 1 !!!) tuple in the join R ⋈ S ----------------------------------------------------------------- */ getNext( ) { /* ============================================================== Note: s already has the current (next ?) tuple of relation S ============================================================== */ while ( true ) { // Loop exits when: // 1. we found a tuple ∈ R that joins with s // 2. R ⋈ S is done (returns NotFound) /* ================================================= Get the next tuple r ∈ R to Join ================================================ */ r = R.getNext(); // Get next tuple in R to perform Join if ( r == NotFound ) { /* --------------------------------------------------- Tuple s has joined with every tuple ∈ R Use next tuple ∈ S in the Join --------------------------------------------------- */ s = S.getNext( ); if ( s == NotFound ) { /* *********************************** We have processed the last tuple ∈ S ********************************** */ return NotFound; // Done !!! } /* =========================================== We have a new tuple s ∈ S Restart R from the beginning =========================================== */ R.Close(); // Close first R.Open( ); // Reset R to beginning r = R.getNext(); // Get current tuple in R } /* ================================================= When we reach here, we have: s = current tuple in S for the Join operation r = current tuple in R for the Join operation ================================================ */ if ( r(Y) == s(Y) ) { return (r,s); // Return next tuple of Join } // Repeat and try the next tuple in R } }
- getNext( ) will
output the
next tuple in
R ⋈ S
- Close( ):
Close( ) { R.Close( ); S.Close( ); }
- Assumption:
- There are M buffers
available
- B(S) ≤ B(R)
- Neither relation
(R nor S)
will fit in the
available buffers
(Otherwise, we can use the efficient one-pass Join algorithm !!!)
- There are M buffers
available
- Block-based
nested loop join
algorithm
in a nutshell:
- The block-based
nested-loop
join algorithm is
based on:
- The one-pass join (⋈) algorithm
- The block-based
nested-loop
join algorithm
accesses the
chunks of
(M−1) blocks of
S
For each chunk:
- Run the one-pass join (⋈) algorithm on that chunk
- The block-based
nested-loop
join algorithm is
based on:
- Organization:
- Use (M − 1) buffers
to read and
index
data blocks from
the smaller relation S
- Use 1 buffer to read data blocks from the larger relation R and compute the Join result
- Use (M − 1) buffers
to read and
index
data blocks from
the smaller relation S
- The "block-based"
nested-loop join algorithm:
while ( S ≠ empty ) { Read M - 1 blocks of S: organize these tuples into a search structure (e.g., hash table)' Rewind R; while ( R ≠ empty ) { Read 1 block (b) of R; for ( each tuple t ∈ block b ) do { Find the tuples s1, s2, ... of S (in the search structure) that join with t Output (t,s1), (t,s2), ... } } }Graphically:
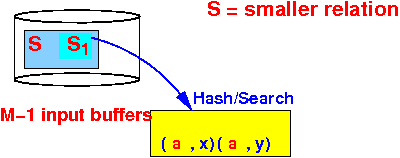
- Step 1-1: read
(M−1) blocks
of the
smaller relation
S and
hash the
tuples:
- Step 1-2:
read the
entire relation R and
compute
R ⋈ S1 (fragment 1 of S):
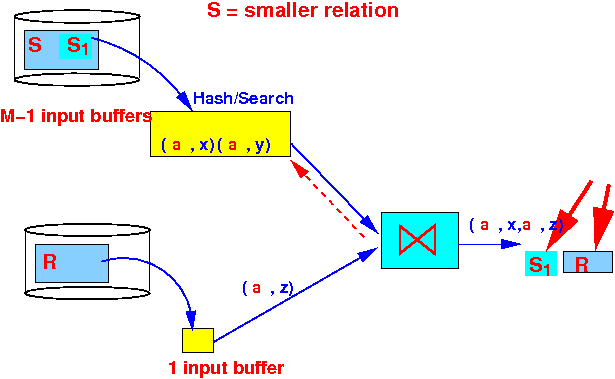
Use the hash table to find the tuples of S !!!
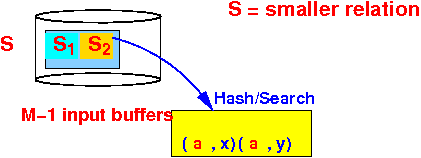
- Step 2-1: read the
next
(M−1) blocks
of the
smaller relation
S and
hash the
tuples:
- Step 2-2:
read the
entire relation R and
compute
R ⋈ S2 (fragment 2 of S):
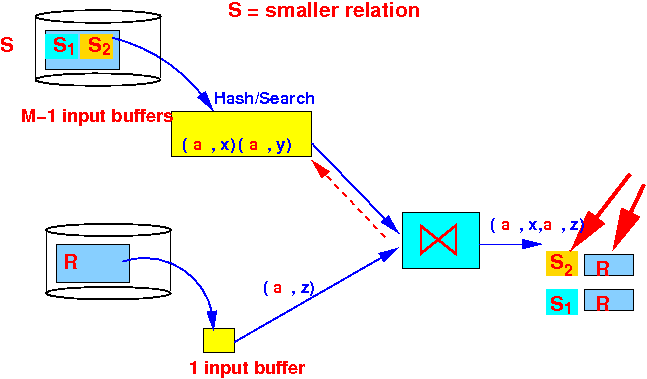
Use the hash table to find the tuples of S !!!
- Repeat until relation S is processed completely
- Step 1-1: read
(M−1) blocks
of the
smaller relation
S and
hash the
tuples:
- # disk I/O used:
(1) The algorithm will read S once: # disk I/Os = B(S) (2) # fragments Si read: B(S)/(M−1) times For each fragment Si, algorithm read R once # disk I/Os = B(S)/(M−1) × B(R)
So: B(S) Total cost = B(S) + ------- B(R) M-1
- Memory requirement:
- M ≥ 2 buffer
- Cost when
using smaller
relation S in
the outer loop:
(Presented previously !!!)
(1) The algorithm will read S once: # disk I/Os = B(S) (2) # fragments Si read: B(S)/(M−1) times For each fragment Si, algorithm read R once # disk I/Os = B(S)/(M−1) × B(R)
So: B(S) Total cost = B(S) + ------- B(R) M-1
- Cost when
using larger
relation R in
the outer loop:
(Presented previously !!!)
(1) The algorithm will read R once: # disk I/Os = B(R) (2) # fragments Ri read: B(R)/(M−1) times For each fragment Ri, algorithm read S once # disk I/Os = B(R)/(M−1) × B(S)
So: B(S) Total cost = B(R) + ------- B(R) M-1