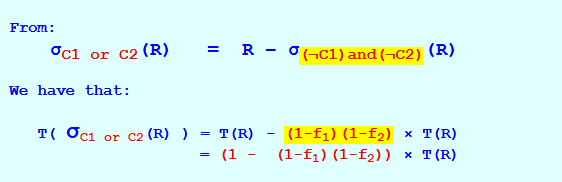---

Estimating the (size of the) result set of a selection (σ)

---

---

---

 

Slideshow:

Overview
 
We will estimate the # tuples in the following σ expressions

A is an attribute and c is a constant value
Estimating the size of the result of σ_{A = c}(R)
 
Estimating the size of the result of σ_{A ≠ c}(R)
 
Estimating the size of the result of σ_{A < c}(R)
 
Estimating the size of the result of σ_{A > c}(R)
 
Estimating the size of the result of σ_{C1 and C2}(R)
 
Given that:

Problem:   estimate the size of   B( σ_{C1 and C2}(R) )   and   T( σ_{C1 and C2}(R) )
Estimating the size of the result of σ_{C1 and C2}(R) - Simplifying Assumption
 
Given that:
 
Estimating the size of the result of σ_{C1 and C2}(R)
 
Given that:
 
If C1 and C2 are statistically independent then:   Probab( C1 and C2 ) = Probab(C1) × Probab(C2)

Estimating the size of the result of σ_{C1 and C2}(R) - Example
 
Estimating the size of the result of σ_{C1 and C2}(R) - Counter example
 
If C1 and C2 are not statistically independent, then do not apply this result !!
Example: a = 10   and   a > 20

Estimating the size of the result of σ_{C1 or C2}(R)
 
Given that:

Problem:   estimate the size of   B( σ_{C1 or C2}(R) )   and   T( σ_{C1 or C2}(R) )
Mathematical pre-requisite
 
Converting σ_{C1 or C2}(R) into an equivalent expression using AND conditions:
Logic law:    not (C1 or C2)   ≡   ( (not C1) and (not C2) )
Therefore:

Estimating the size of the result of σ_{C1 or C2}(R) - Simplifying Assumption
 
Given that:
 
Estimating the size of the result of σ_{C1 and C2}(R)
Given that:

Previously, we have derived this equality:

Therefore: (applying statistical indepencence of ¬C1 and ¬C2)

Estimating the size of the result of σ_{C1 and C2}(R) - Example
 
❮ ❯



---

---

---

---

• Intro

  • Cases that we will study:

    σ A = c (R) σ A < c (R) σ C1 and C2 (R)              σ C1 or C2 (R)

  ---

  ---

  ---

  ---

• S = σ _{A = c} (R)
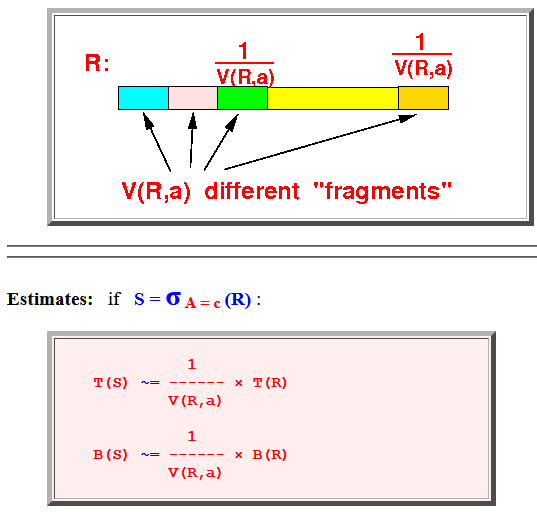
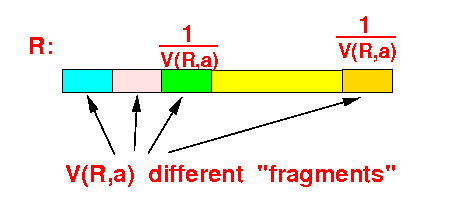
  • Situation:

    ---

    ---

  • Estimates:   if   S = σ _{A = c} (R) :

    1 T(S) ~= ------ × T(R) V(R,a) 1 B(S) ~= ------ × B(R) V(R,a)

  ---

  ---

  ---

  ---

• Related: S = σ _{A ≠ c} (R)
  • Fact:

    σA ≠ c(R) ∪ σA = c(R) = R <==> σA ≠ c(R) = R − σA = c(R)

    ---

    Therefore: if   S = σ _{A ≠ c} (R) :

    1 T(S) ~= T(R) × ( 1 - ------ ) V(R,a) 1 B(S) ~= B(R) × ( 1 - ------ ) V(R,a)

  ---

  ---

  ---

  ---

• S = σ _{A < c} (R)
  • Heuristic used to estimate the result set of σ _{A < c} (R) is use the 50/50 rule:

    1 T(S) ~= --- × T(R) 2 1 B(S) ~= --- × B(R) 2

    ---

    ---

  • The text book proposes the following estimate:

    1 T(S) ~= --- × T(R) 3 1 B(S) ~= --- × B(R) 3

    We will go with the text book proposal as estimate for this course.

  ---

  ---

  ---

  ---

• Related: S = σ _{A > c} (R)
  • We will also use:

    1 T(S) ~= --- × T(R) 3 1 B(S) ~= --- × B(R) 3

    as an estimate for S = σ _{A > c} (R) !!!

    (The logic is people are always more interested in finding out about less common facts).

  ---

  ---

  ---

  ---

• S = σ _{C1 and C2} (R)
  • Given:

    B( σC1(R) ) = f1 B( R ) T( σC1(R) ) = f1 T( R ) B( σC2(R) ) = f2 B( R ) T( σC2(R) ) = f2 T( R )

    ---

  • Simplifying assumption:

    The conditions C1 and C2 are (statistically) independent

    ---

    ---

  • Then:

    S = σC1 and C2(R) = σC1 ( σC2(R) ) T(S) = f1 × f2 T(R) // From the independence assumption // ⇒ we use the product rule of Probability Theory B(S) = f1 × f2 B(R)

    ---

    ---

  • Example:

    S = σ b=10 and a <20 (R) It is given that: V(R,a) = 50 Estimate the size of the result set S: S1 = σb=10(R) ⇒ T(S1) ~= 1/50 × T(R) S2 = σa<20(R) ⇒ T(S2) ~= 1/3 × T(R) Then: T(S) = (1/50) × (1/3) × T(R) = 1/150 × T(R)

    ---

  • Warning: use common sense when you apply any rule !!!

    When the conditions C1 and C2 are dependent, we must not use the independence assumption !!! Example: S = σa=10 and a >20(R) Because: a=10 and a>20 are contradictory, we have: T(S) = 0 !!!

  ---

  ---

  ---

  ---

• S = σ _{C1 or C2} (R)
  • Given:

    B( σC1(R) ) = f1 B( R ) T( σC1(R) ) = f1 T( R ) B( σC2(R) ) = f2 B( R ) T( σC2(R) ) = f2 T( R )

    Problem:

    What is the size of B( σ C1 or C2(R) )   (and T( σ C1 or C2(R) )) ???

    ---

    ---

  • Preparatory step:

    σC1 or C2(R) ∪ σ¬(C1 or C2)(R) = R ⇒   σC1 or C2(R) = R − σ¬(C1 or C2)(R)   = R − σ(¬C1)and(¬C2)(R)

    ---

  • Simplifying assumption:

    The conditions (¬C1) and (¬C2) are (statistically) independent

    Then:

    From:   σC1 or C2(R) = R − σ(¬C1)and(¬C2)(R) We have that: T( σC1 or C2(R) ) = T(R) - (1-f1)(1-f2) × T(R)   = (1 - (1-f1)(1-f2)) × T(R)

    ---

    ---

  • Example:

    S = σ a=10 or a <20 (R) It is given that: V(R,a) = 50 Estimate the size of the result set S: S1 = σa=10(R) ⇒ T(S1) ~= 1/50 × T(R) S2 = σa<20(R) ⇒ T(S2) ~= 1/3 × T(R) Then: T(S) = ( 1 - (1 - 1/50)(1 - 1/3) ) × T(R)