- Two Phase Locking (2PL):
- Two Phase Locking =
a ordering of
locking operations in a
transaction
where:
- All the lock operations precedes all the unlock operations
- Two Phase Locking =
a ordering of
locking operations in a
transaction
where:
- Schematically:
Transaction: lock(A) ... lock(B) ... ... lock(X) ... ... unlock(B) ... unlock(X) ... unlock(A) ...The 2 phases:
- Phase 1:
- Acquire locks
- Phase 2:
- Release locks
- Phase 1:
- Example:
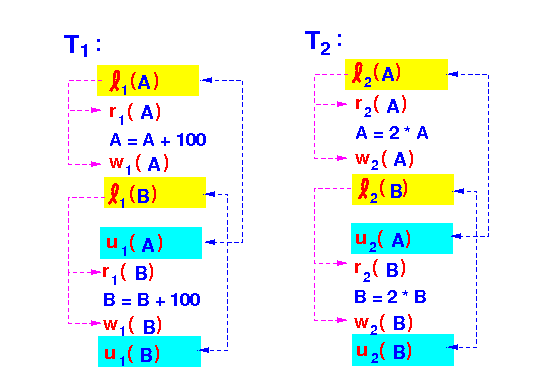
Notice:
- All lock operations precedes all unlock operations !!!
Execution results in consistent database state:
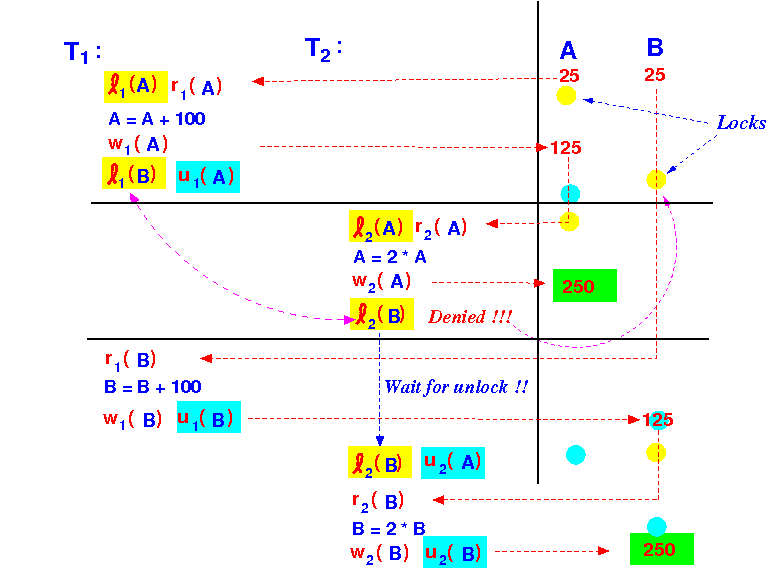
- Counter example:
non-2PL transactions
can result in
inconsistsent DB state
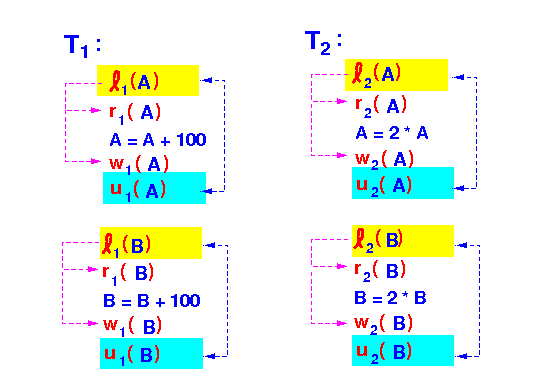
Notice:
- The transactions are
not
two-phase !!!
- The unlock operation ui(A) happens before an lock operation (ℓi(B)
Execution results in INconsistent database state:
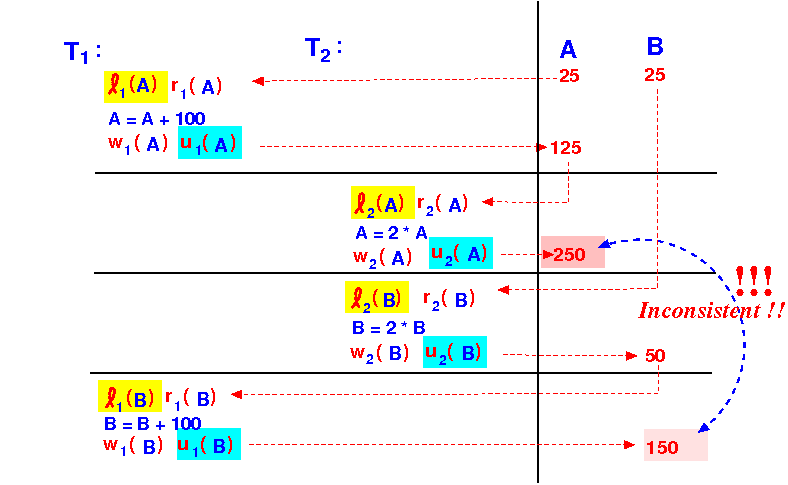
- The transactions are
not
two-phase !!!
- Theorem:
- Let
T1,
T2, ...
Tn be
n transactions that
obey the
2PL rule:
- T1, T2, ... Tn do not execute any unlock operation before a lock operation
- Let Sn = a
schedule of the
(read, write, lock and unlock) operations
found in
T1,
T2, ...
Tn
(that obey the
locking semantics !!!)
- Then:
- Sn is a conflict-serializable schedule
- Let
T1,
T2, ...
Tn be
n transactions that
obey the
2PL rule:
- Proof: by induction
- The base case:
n = 1
- T1 is
1 transaction that
obey the
2PL rule
- S1 = a
schedule of the
(read, write, lock and unlock) operations
found in
T1
- Then:
- S1 is
serial schedule
- Therefore, S1 is trivially a conflict-serializable schedule
- S1 is
serial schedule
- T1 is
1 transaction that
obey the
2PL rule
- The induction case:
- Induction asumption:
- Every schedule Sn−1 of the (read, write, lock and unlock) operations found in n−1 transactions T1, T2, ... Tn−1 (that obey the locking semantics !!!) is conflict-serializable
- Let Sn = a
schedule of the
(read, write, lock and unlock) operations
found in n transactions
T1,
T2, ...
Tn
(that obey the
locking semantics !!!)
- We must show that Sn is a conflict-serializable schedule
- Let ui(•)
be the first unlock operation
found in
schedule Sn:
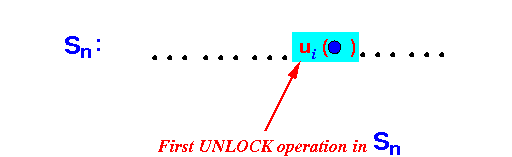
Claim:
- We can move all the operations ri(•) and wi(•) by transaction Ti forward in schedule Sn without passing any conflicting operation by another transaction
- Proof of the claim:
- Consider an aribitrary operation by transaction Ti: e.g., wi(Y)
- Consider
an arbitrary conflicting operation
by some other transaction Tj: e.g.,
wj(Y)
- We will prove that
this ordering of
operations is
not possible:
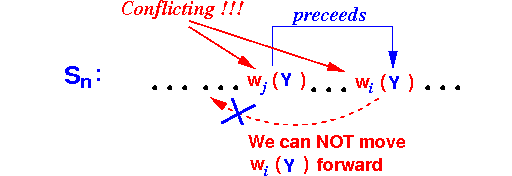
- In order for this ordering to be
legal
(obey the locking rules),
we must have
the following lock/unlock sequence on
DB element Y:
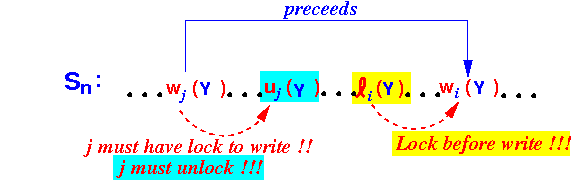
- Since every transaction is
2PL, the
unlock operations must
follow the
lock operation
ℓi(X):
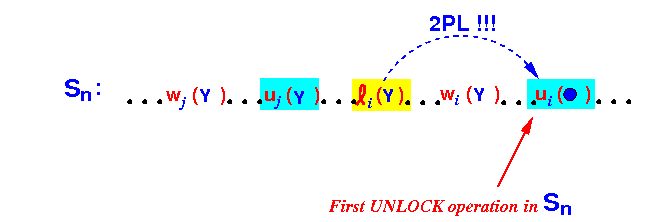
Theorefore, in schedule Sn, the transcation j will perform an unlock operation before transcation i:
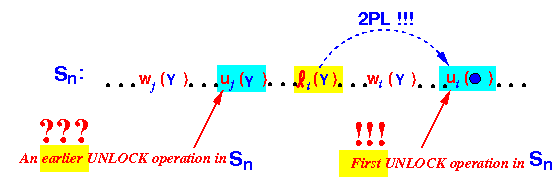
This is a contradiction of the fact that transcation i performs the first unlock operation !!
So this claim is true:
- We can move
all
the operations
ri(•) and wi(•)
by
transaction Ti
forward in
schedule Sn
without passing
any
conflicting operation by
another transaction:
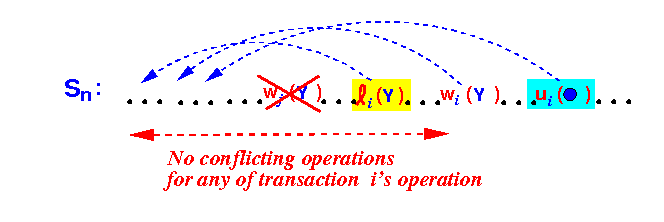
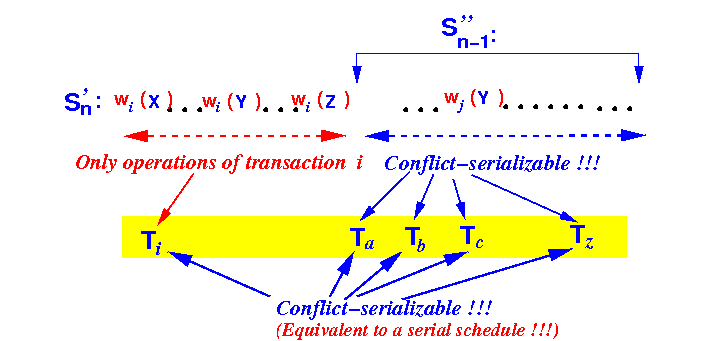
Therefore, the schedule Sn is conflict-equivalent to the following schedule S'n:
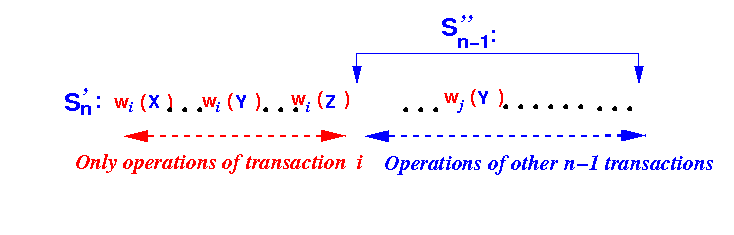
Schedule S'n consists of:
- All operations by
transaction Ti
(the first transaction that performs an
unlock operation
- A sub-schedule S''n−1 of n−1 (2PL) transactions
By the Induction asumption:
- Every schedule
Sn−1 of the
(read, write, lock and unlock) operations
found in n−1 transactions
T1,
T2, ...
Tn−1
(that obey the
locking semantics !!!) is
conflict-serializable
- Therefore:
the sub-schedule S''n−1
is
conflict-serializable:
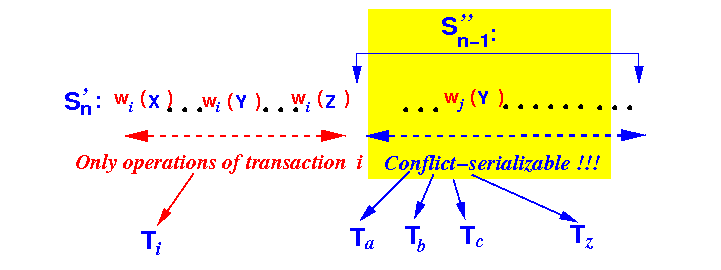
Consequently:
- The schedule Sn
is
conflict-serializable:
Q.E.D.
- Induction asumption: