---

Summary: Analysis of the Carrier Sense Multiple Access (CSMA) scheme

---

• Unslotted Aloha
  • When is a transmission successful:

    The transmission x is successful: if and only if: There are no transaction attempts that begins (= arrives) during the time interval (t-1, t+1]

    ---

  • Therefore:

    Probab[ a transmission attempt is successful ] = Probab[ 0 arrivals in the period (t-1,t+1] ] = Prabab[ 0 arrivals in 2 time units ] (G × 2)0 e(−G × 2) = ---------------- 0! = e−2G

    G = offered load

    ---

  • Throughput:

    Throughput = #transmission attempts × Probab[ attempt is successful ] = G × e−2G

  ---

  ---

• Slotted Aloha
  • When is a transmission successful:

    The transmission x is successful: if and only if: There are no transaction attempts that begins (= arrives) during the time interval (t-1, t]

    ---

  • Therefore:

    Probab[ a transmission attempt is successful ] = Probab[ 0 arrivals in the period (t-1,t] ] = Prabab[ 0 arrivals in 1 time units ] (G × 1)0 e(−G × 1) = ---------------- 0! = e−G

    G = offered load

    ---

  • Throughput:

    Throughput = #transmission attempts × Probab[ attempt is successful ] = G × e−G

  ---

  ---

• Non-persistent CSMA
  • Non-persistent CSMA protocol:

    Station listens before transmitting packet If station detects idle channel, it transmits immediately Otherwise (station detects busy channel), the station waits a random amount of time and tries again

    ---

  • Simplifying assumptions:

    All packets have the same length T (So the transmission time for any packet is the same duration)              Assume that the propagation delay between any two nodes is equal to τ seconds Like this: Define: τ a = --- T which is the normalized propagation delay The packet arrival process is a Poisson process with rate λ The offered load (new arrivals and retransmission attempts combined) is also Poisson distributed with rate g (We will see that the offered load g is dependent on the arrival rate λ)

    ---

  • Throughput computation of the non-persistent CSMA protocol:

  • Throughput of the unslotted non-persistent CSMA protocol:

    U Snon-persistent CSMA = ------ ...... (1) B + I

  • where:

    B = the average duration of a busy period in the non-persistent CSMA cycle A busy period can be useful (i.e., successful transmission) or not useful (i.e., collision) U = the average duration of a busy period that is useful in the non-persistent CSMA cycle I = the average duration of a idle period in the non-persistent CSMA cycle

  ---

  ---

• Average length of an idle period (I)
  • Idle period ends with an arrival:

  • Cumulative density function of an idle period I is:

    Ҏ[ I ≤ x ] = 1 - Ҏ[ I > x ] = 1 - Ҏ[ no packet arrives in x sec ] (gt)k Ҏ[ k arrivals in t sec ] = ---- e-gt k! (gx)0 Ҏ[ I ≤ x ] = 1 - ---- e-gx 0! <=> Ҏ[ I ≤ x ] = 1 - e-gx

    ---

  • Average duration of an idle period I:

    I = 0∫∞ x fI(x) dx 1 ==> I = --- g

  ---

  ---

• Average length of a useful period U
  • Average length of the useful period:

    U = T × Ҏ[ transmission successful ] + 0 × (1 - Ҏ[ transmission successful ])

    ---

  • Ҏ[ transmission successful ]:

    Ҏ[ transmission successful ] = Ҏ[ 0 arrivals within "vulnerable period" ] = Ҏ[ 0 arrivals within τ sec ] (gt)k Ҏ[ k arrivals in t sec ] = ---- e-gt k! (gτ)0 Ҏ[ transmission successful ] = ----- e-gτ 0! <=> Ҏ[ transmission successful ] = e-gτ

    ---

  • Therefore:

    U = T × Ҏ[ transmission successful ] + 0 × (1 - Ҏ[ transmission successful ]) = T × e-gτ + 0 × (1 - e-gτ) U = T × e-gτ

  ---

  ---

• Average length of busy period B
  • Average length of a busy period B

    Notes:

    B = T + τ + y where: T = length of a packet transmission (constant) τ = (max) end-to-end delay (constant) y = time lag of the last transmission (random) From Theory of probability: E[B] = E[ T + τ + y ] <=> E[B] = T + τ + E[y] <=> B = T + τ + y

    ---

  • The random variable y is an hybrid (mixed discrete/continuous) random variable:

    fy(t) = e-gτ × &delta(t) + g e-g(τ-t) (with t ∈ [0, τ))

    ---

  • The expected value E[y]:

    E[y] = -∞∫∞ t × fy(t) dt = 0∫τ t × fy(t) dt Split off the discontinuous point t = 0           => E[y] = 0 × Ҏ[ y = 0 ] + 0+∫τ t × fy(t) dt = 0 × e-gτ + 0+∫τ t × g e-g(τ-t) dt 1 - e-gτ = τ - --------- g

    ---

  • Therefore:

    1 - e-gτ B = T + τ + ( τ - --------- ) g 1 - e-gτ = T + 2τ - --------- g

    ---

  • Summary:

    1 I = --- g U = T × e-gτ 1 - e-gτ B = T + 2τ - --------- g

    ---

  • Therefore:

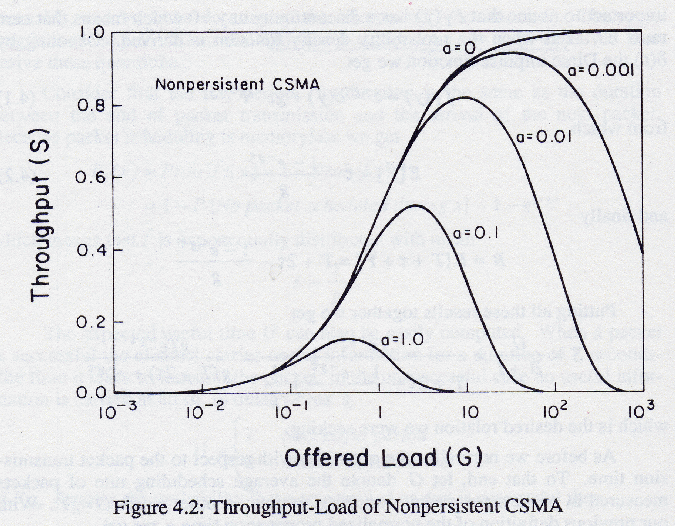
    U S = ------- B + I gT × e-agT ==> S = ------------------- gT(1 + 2a) + e-agT

  • Performance graphs:

  ---

  ---

  ---

  ---

• 1-persistent CSMA
  • 1-persistent CSMA protocol:

    Station listens before transmitting packet If station detects idle channel, it transmits immediately Otherwise (station detects busy channel), the station waits until transmission ends and transmits packet

    ---

  • Definitions of the different states:

    State 0 = the number of packet arrivals at the start of the transmission period is equal to 0 State 1 = the number of arrivals at the start of the transmission period is equal to 1 State 2 = the number of arrivals at the start of the transmission period is equal to 2

    ---

  • The state transition diagram of the 1-persistent (unslotted) CSMA protocol:

  • Example state transitions:

    ---

  • Preliminary Throughput expression of the unslotted 1-persistent CSMA protocol:

    π0T × Ҏ[ success in T0 ] + π1T × Ҏ[ success in T1 ] + π2T × Ҏ[ success in T2 ] S = --------------------------------------------------------------------------------- π0T0 + π1T1 + π2T2 π0T × 0 + π1T × Ҏ[ 0 arrival in τ sec ] + π2T × 0 <=> S = ---------------------------------------------------------- π0T0 + π1T1 + π2T2 π1T × e-gτ <=> S = --------------------- (T = packet length) π0T0 + π1T1 + π2T2

    ---

    ---

  • T₀ = idle period:

    1 T0 = --- (Idle period) (See: click here) g

  • The average duration of a type 1 period and type 2 period is:

    E[T1] = T + τ + E[y] E[T2] = E[T1] Result: 1 - e-gτ T1 = T + 2τ - --------- g 1 - e-gτ T2 = T + 2τ - --------- g

    ---

    ---

  • Solving &pi₀, &pi₁ and &pi₂:

    p10 π0 = --------- 1 + p10 p10 + p11 π1 = ----------- 1 + p10 1 - p10 - p11 π2 = -------------- 1 + p10

    where:

    p10 = Ҏ[ 0 arrivals in (T + y) sec ] = (1 + gτ) e-g(T+τ)

    p11 = Ҏ[ 1 arrivals in (T + y) sec ] = g e-g(T+τ) (T + gτ(T + τ/2))

    ---

  • Throughput of 1-persistent CSMA:

    gT e-g(T+2τ) [ 1 + gT + gτ(1 + gT + gτ/2) ] S = -------------------------------------------- g(T + 2τ) - (1 - e-gτ) + (1 + gτ)e-g(T+τ)