Suppose we need to solve some problem of size n:
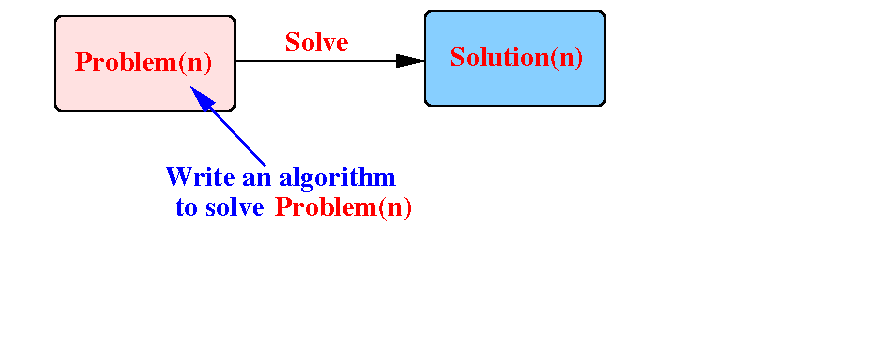
Consider the other identical (but) smaller problems:
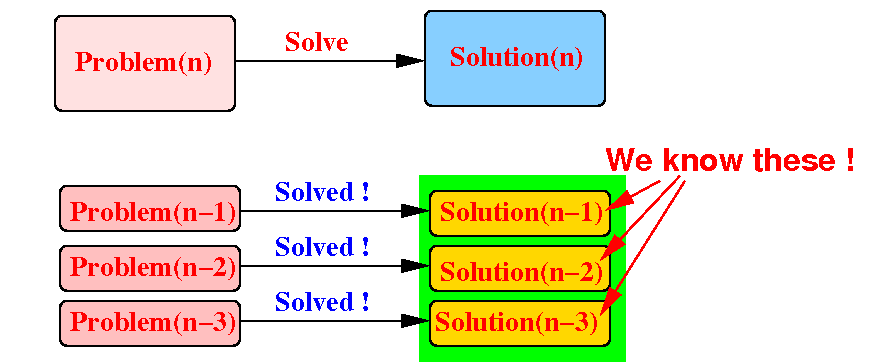
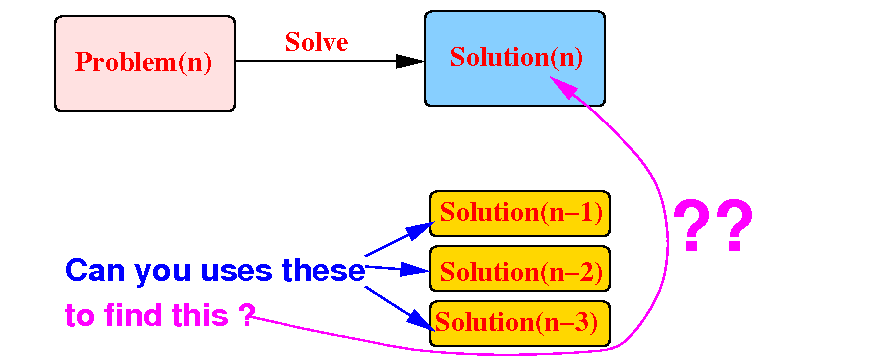
Suppose that we (already) have the solutions for all the smaller problems, i.e.: we do not need to solve them
If we can use the solutions of the smaller problems to find Solution(n) (= solution of the original problem):
Then: we can use recursion to solve the Problem(n)
The main difficulty of using recursion is to find a way to use the smaller solutions to construct Solution(n):
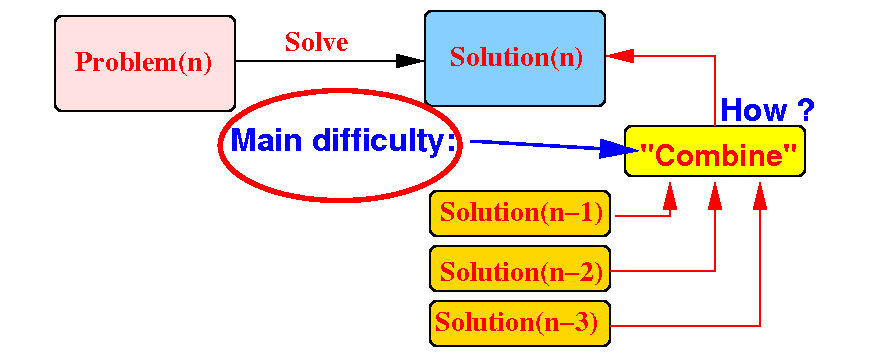
The "combine" step is problem-dependent
Suppose we need to compute factorial(10):
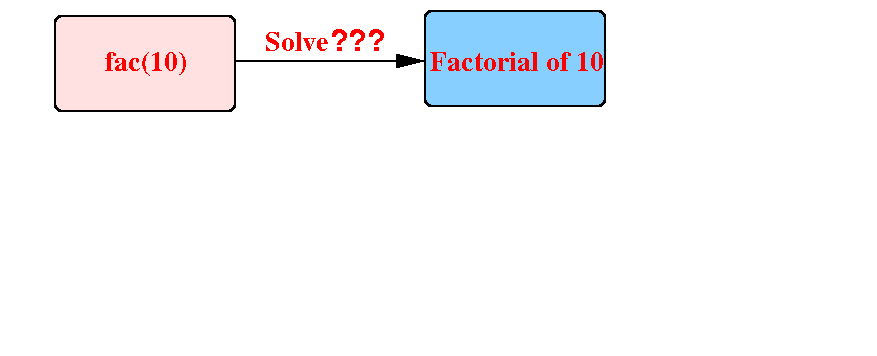
Suppose we have the solution for the smaller problem factorial(9):
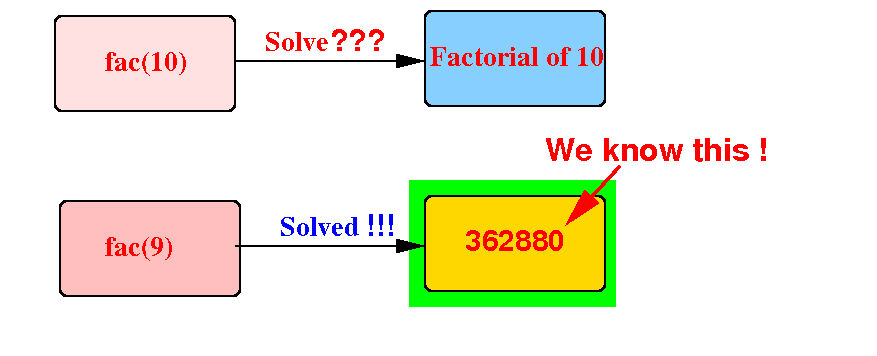
Question: can we use 362880 to compute factorial(10) ?
We can compute factorial(10) using the value 362880 as follows: 10! = 10 × 362880
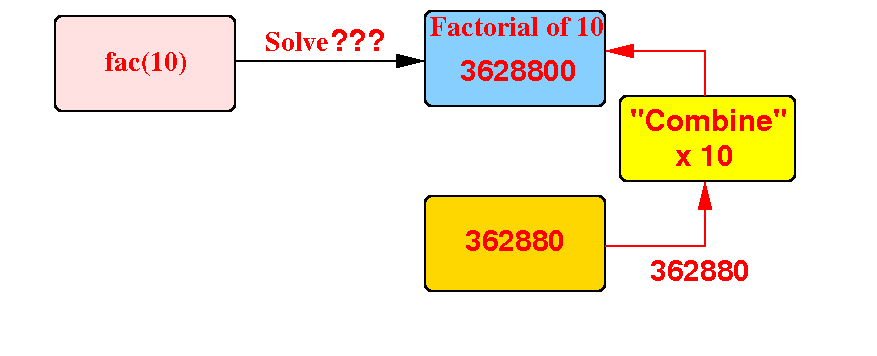
Therefore: we can use recursion to solve the factorial problem
How to write factorial( ) as a divide-and-conquer algorithm:
int factorial(int n)
{
}
|
Let's write the factorial( ) method again, but this time exposing the divide-and-conquer technique
The base case(s) is unchanged:
int factorial(int n)
{
if ( n == 0 )
return 1; // Base case
}
|
In the divide step, we delegate someone else to solve some smaller problem(s) that can be used to solve the original problem
Divide: tell someone else to solve the smaller problem factorial(n-1):
int factorial(int n)
{
int helpSol; // Solution to the smaller problem
if ( n == 0 )
return 1; // Base case
else
{
helpSol = factorial(n-1); // Tell someone to solve this
// (We receive the solution in helpSol)
}
}
|
Next: in the conquer step, we use helpSol to find solution for the original problem
Conquer: we solve factorial(n) using helpSol:
int factorial(int n)
{
int helpSol; // Solution to the smaller problem
int mySol; // Solution to my problem
if ( n == 0 )
return 1; // Base case
else
{
helpSol = factorial(n-1); // Tell someone to solve this
// (We receive the solution in helpSol)
mySol = n*helpSol; // Solve original problem using the
// solution of the smaller problem
}
}
|
Finally, we return the solution...
The factorial(n) method written as a divide-and-conquer algorithm:
int factorial(int n)
{
int helpSol; // Solution to the smaller problem
int mySol; // Solution to my problem
if ( n == 0 )
return 1; // Base case
else
{
helpSol = factorial(n-1); // Tell someone to solve this
// (We receive the solution in helpSol)
mySol = n*helpSol; // Solve my problem using the
// solution of the smaller problem
return(mySol);
}
}
|
DEMO: demo/07-recursion/01-factorial/DivideAndConquer.java
You must distinguish between:
|
I like to use the roles you and your helper to make the distinction:
int factorial(int n) <--- This factorial( ) represents "YOU" { int helpSol; int mySol; if ( n == 0 ) return 1; else { helpSol = factorial(n-1); <--- This factorial( ) is your "helper" // This factorial( ) solves a smaller problem mySol = n*helpSol; return (mySol); } } |
What happens in recursion: recursion will run another copy of the same method
Previously: the factorial(n) method written as a divide-and-conquer algorithm:
int factorial(int n)
{
int helpSol; // Solution to the smaller problem
int mySol; // Solution to my problem
if ( n == 0 )
return 1; // Base case
else
{
helpSol = factorial(n-1); // Tell someone to solve this
// (We receive the solution in helpSol)
mySol = n*helpSol; // Solve my problem using the
// solution of the smaller problem
return(mySol);
}
}
|
We can simplify the algorithm with substitution...
Substitute helpSol with factorial(n-1) :
int factorial(int n)
{
|
We can simplify the algorithm further with short-circuiting some computations...
Return the result n*factorial(n-1) directly:
int factorial(int n)
{
|
We can simplify the algorithm with substitution...
Result: we get back the original factorial( ) method
int factorial(int n)
{
if ( n == 0 )
return 1; // Base case
else
{
return n*factorial(n-1); // Solve my problem using the
// solution of the smaller problem
}
}
|