MST and TSP
Due: written 5pm Friday 3/30, program 11:59pm Wednesday 4/4
Homework 4
If I get written hw1 graded and back to you by Monday, then these are
due 5pm Friday, on paper. Otherwise you do not have to do these,
except for review. Or alternatively, you can do them as a ``makeup''
for a previous written homework (you have to tell me which one).
Suppose 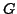 is a connected undirected graph, and each edge
is a connected undirected graph, and each edge
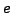 has a non-negative length
has a non-negative length 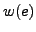 . Let
. Let 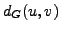 denote the
shortest path distance between vertices
denote the
shortest path distance between vertices 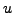 and
and 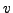 in graph
in graph 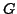 (if
they are not connected, say the distance is
(if
they are not connected, say the distance is 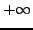 ). . Also,
suppose
). . Also,
suppose 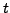 is a real number,
is a real number, 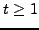 . Consider this algorithm:
. Consider this algorithm:
xxxxxx xxxx
Let 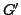 contain all the vertices of
contain all the vertices of 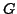 , but (initially) no edges.
, but (initially) no edges.
Let 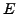 be the set of edges in
be the set of edges in 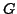 , sorted by weight.
, sorted by weight.
For each edge 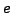 in
in 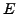 :
:
Let 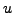 and
and 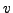 be the endpoints of
be the endpoints of 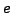 .
.
If 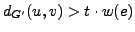 , then add
, then add 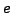 to
to 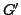 .
.
In the following questions, 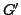 denotes the final version of
denotes the final version of 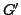 .
.
Argue that for any 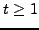 ,
, 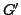 contains the MST of
contains the MST of 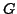 .
.
Argue that for any pair of vertices 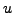 and
and 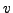 ,
,
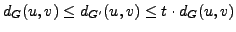 .
.
Suppose we have 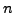 points in the plane. Between any two
points, we allow an edge whose weight is the Euclidean distance
between its endpoints (think of the edge as a line segment). Their
EMST (Euclidean MST) is their minimum spanning tree using such
edges.
points in the plane. Between any two
points, we allow an edge whose weight is the Euclidean distance
between its endpoints (think of the edge as a line segment). Their
EMST (Euclidean MST) is their minimum spanning tree using such
edges.
For simplicity, suppose no 4 of the 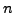 points lie on a circle. Their
Delaunay triangulation is a graph on the points, containing
edge
points lie on a circle. Their
Delaunay triangulation is a graph on the points, containing
edge 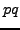 whenever there is a circle with points
whenever there is a circle with points 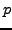 and
and 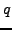 on its
boundary, but no point in its interior.
on its
boundary, but no point in its interior.
Argue that the Delaunay triangulation is planar. That is, edges do not intersect except at their endpoints.
Argue that the Delaunay triangulation contains the
Euclidean MST.
Suppose we have the Delaunay triangulation. Argue that
we can compute the EMST in 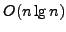 time.
time.
Suppose we again have 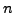 points in the plane.
We consider geometric graphs: the vertices are the
points in the plane.
We consider geometric graphs: the vertices are the 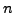 points,
and the weight of each edge is its length.
points,
and the weight of each edge is its length.
Fix some parameter 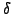 , and build a graph
, and build a graph
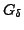 containing all edges of length at most
containing all edges of length at most 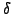 .
Argue that if
.
Argue that if 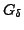 is connected, then its MST is the EMST.
is connected, then its MST is the EMST.
Fix some integer 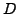 , and build graph
, and build graph 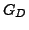 containing,
for each vertex
containing,
for each vertex 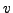 , edges to its
, edges to its 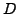 closest neighbors. Argue,
by example, that even if
closest neighbors. Argue,
by example, that even if 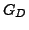 is connected, its MST may not
be the EMST.
is connected, its MST may not
be the EMST.
The homework files are not quite ready, expect them ready by Monday.
The basic idea is this: I will give you a program which computes a
geometric graph on points in the plane (but by a rather slow method).
From that geometric graph, we can compute the MST (by Kruskal's
algorithm in the book). Then from the MST, I want you to compute
an approximate solution to the TSP.
For extra credit, you may also try to speed up the MST computation.
More details Monday.
contain all the vertices of
, but (initially) no edges.
be the set of edges in
, sorted by weight.
in
:
and
be the endpoints of
.
, then add
to
.
![]() points lie on a circle. Their
Delaunay triangulation is a graph on the points, containing
edge
points lie on a circle. Their
Delaunay triangulation is a graph on the points, containing
edge ![]() whenever there is a circle with points
whenever there is a circle with points ![]() and
and ![]() on its
boundary, but no point in its interior.
on its
boundary, but no point in its interior.