Using a 2 dimensional grid in GPU matrix multiplication

Matrices are 2 dimensional structures: 

       +-              -+          +-              -+
       |A11    A12    A13|          |B11    B12    B13|
   A = |A21    A22    A23|      B = |B21    B22    B23|
       |A31    A32    A33|          |B31    B32    B33|
       +-              -+          +-              -+

 Then:

              +-              -+
              |C11    C12    C13|
   C =  A*B = |C21    C22    C23|
              |C31    C32    C33|
              +-              -+

 where:

    Cij = ∑k=0..N-1 AikBkj      
 
        (for i = 0, 1, .., N-1 and j = 0, 1, ..., N-1)

Using a 2 dimensional grid in GPU matrix multiplication

Matrix elements are organized using a 2 dimensional index: 

   int   N = ...;       // Some pre-defined value
   float A[N][N];       // Matrix 1
   float B[N][N];	// Matrix 2
   float C[N][N];	// Output matrix


   //CPU matrix mult alg for static 2-dimensional arrays
   for (int i = 0; i < N; i++)
      for (int j = 0; j < N; j++)
      {
         /* ---------------------------------
            Compute the matrix element
                    Cij = ∑k=0..N-1 AikBkj     
            --------------------------------- */
         C[i][j] = 0.0;

         for (int k = 0; k < N; k++)            
            C[i][j] = C[i][j] + A[i][k]*B[k][j];  // 1 vector product
      }

Previously, the CUDA program launches a 1 dimensional grid of threads

The previous CUDA program launches a 1-dimensional grid (as <<< B,T >>>) to perform the matrix multiplication: 

int main(int argc, char *argv[])
{
  int N = Matrix size
  int T = # threads per thread block (user choice)
  int B = ceil((float) N*N / T ); // # thread blocks needed 

  float *a, *b, *c;

  /* =======================================
     Allocate 3 shared matrices (as arrays)
     ======================================= */
  cudaMallocManaged(&a, N*N*sizeof(float));
  cudaMallocManaged(&b, N*N*sizeof(float));
  cudaMallocManaged(&c, *sizeof(float));

  // initialize x and y arrays (code omitted)

  matrixMult<<< B, T >>>(a, b, c, N);   // Launch kernel
}

It's more natural to use a 2 dimensional grid to execute matrix operations !!!

Designing a 2-dimensional grid for matrix multiplicaton

The number of matrix elements in a N × N matrix is N2:

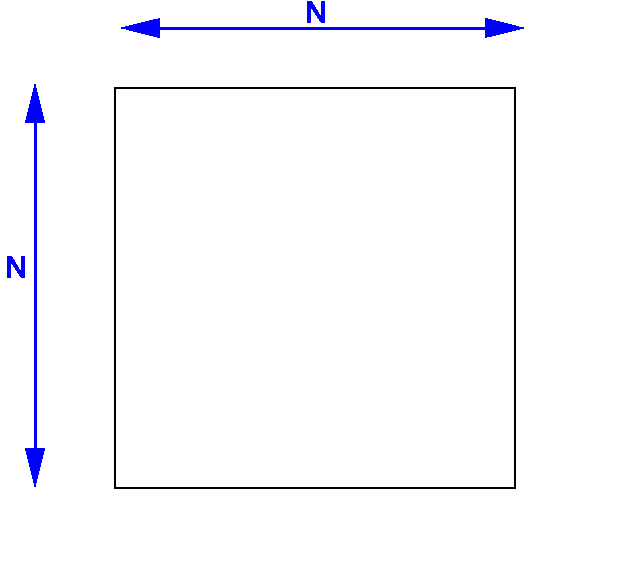
We will divide the matrix up into squares...

Designing a 2-dimensional grid for matrix multiplicaton

We will create thread block that is a square:

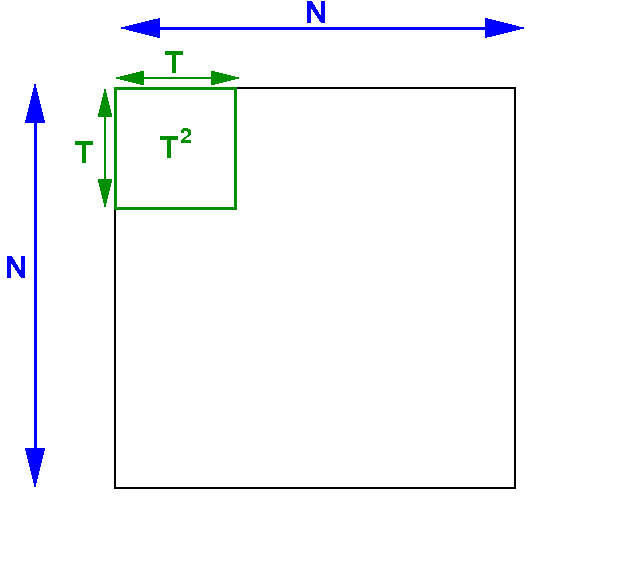
Each thread block will contain T2 threads
Note:   T2 ≤ 1024  or  T ≤ 32

Designing a 2-dimensional grid for matrix multiplicaton

The number of rows and columns of the grid is B:

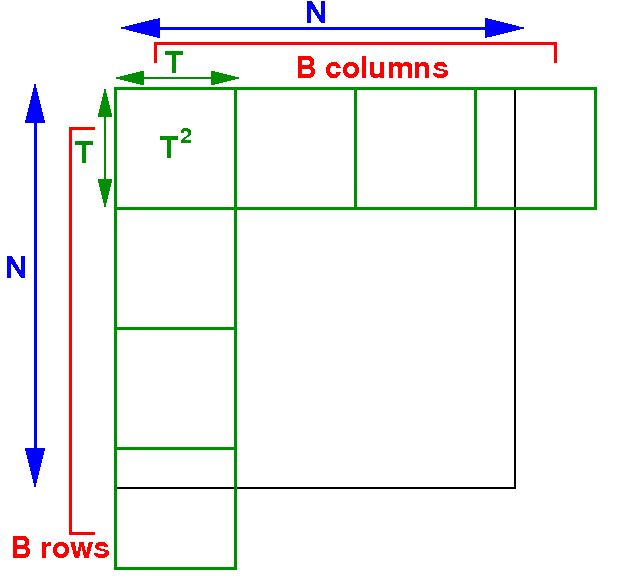
Question:   what is the value of B to accommodate a N × N matrix ?

Designing a 2-dimensional grid for matrix multiplicaton

The number of blocks that you need to use to span an N × N matrix is:

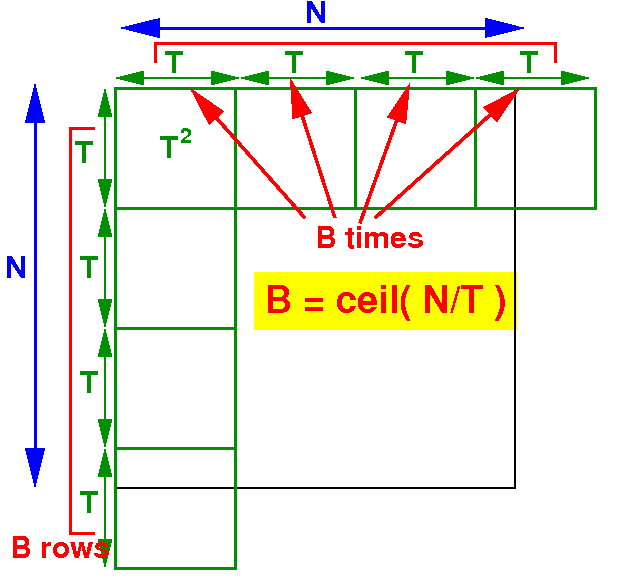
Answer:   we need B × B blocks where B = ceil(N/T)

The CUDA matrix multiplication algorithm - CPU part

The CPU code:   (1) allocate arrays and (2) then launches the threads: 

int main(int argc, char *argv[])
{
  int N = ..; // N × N matrix

  

 

  
    
    
 
 
  

  

  
}

N will be specified by the user input

The CUDA matrix multiplication algorithm - CPU part

T = the number of threads in a block in one dimension: 

int main(int argc, char *argv[])
{
  int N = ..; // N × N matrix
  int T = ..; dim3 blockShape = dim3(T, T); // TxT threads/block
 

 


  
    
  
 
 

  

  
}

 

The CUDA matrix multiplication algorithm - CPU part

We will create B2 thread blocks to perform the matrix multiplication: 

int main(int argc, char *argv[])
{
  int N = ..; // N × N matrix
  int T = ..; dim3 blockShape = dim3(T, T); // TxT threads/block
  int B = ceil( (double)N/T ); dim3 gridShape  = dim3(B, B);
  

  
    
    
 
  
  

  


  
}

Each dimension will have ≥ N threads !!!

The CUDA matrix multiplication algorithm - CPU part

We define the reference variables to help us allocate the shared arrays: 

int main(int argc, char *argv[])
{
  int N = ..; // N × N matrix
  int T = ..; dim3 blockShape = dim3(T, T); // TxT threads/block
  int B = ceil( (double)N/T ); dim3 gridShape  = dim3(B, B);

  float *a, *b, *c;


    
    
 
  
  

 

 
}

(This is CUDA syntax... i.e, how CUDA provide the dynamic shared array to us)

The CUDA matrix multiplication algorithm - CPU part

Allocate the 3 shared matrices (as 1-dim arrays): 

int main(int argc, char *argv[])
{
  int N = ..; // N × N matrix
  int T = ..; dim3 blockShape = dim3(T, T); // TxT threads/block
  int B = ceil( (double)N/T ); dim3 gridShape  = dim3(B, B);

  float *a, *b, *c;

  /* =======================================
     Allocate 3 shared matrices (as arrays)
     ======================================= */
  cudaMallocManaged(&a, N*N*sizeof(float));
  cudaMallocManaged(&b, N*N*sizeof(float));
  cudaMallocManaged(&c, N*N*sizeof(float));

  // initialize x and y arrays (code omitted)


}

(This is CUDA syntax... i.e, how CUDA provide the dynamic shared array to us)

The CUDA matrix multiplication algorithm - CPU part

Launch (at least) N2 threads as <<< gridShape, blockShape >>> to perform the matrix multiplication: 

int main(int argc, char *argv[])
{
  int N = ..; // N × N matrix
  int T = ..; dim3 blockShape = dim3(T, T); // TxT threads/block
  int B = ceil( (double)N/T ); dim3 gridShape  = dim3(B, B);

  float *a, *b, *c;

  /* =======================================
     Allocate 3 shared matrices (as arrays)
     ======================================= */
  cudaMallocManaged(&a, N*N*sizeof(float));
  cudaMallocManaged(&b, N*N*sizeof(float));
  cudaMallocManaged(&c, N*N*sizeof(float));

  // initialize x and y arrays (code omitted)

  matrixMult<<< gridShape, blockShape >>>(a, b, c, N); // 2 dim grid
}

We will write the kernel code for matrixMult( ) next...

The CUDA matrix multiplication algorithm - GPU part

First, compute a unique ID (i,j) for each thread within the <<< B, T >>> configuration: 

__global__ void matrixMult(float *A, float *B, float *C, int n)
{
   int i = blockIdx.x*blockDim.x + threadIdx.x;
   int j = blockIdx.y*blockDim.y + threadIdx.y;


   
          
      
           
        


        



}

 

The CUDA matrix multiplication algorithm - GPU part

The thread (i,j) on the GPU must compute the element C[i][j] in the output matrix: 

__global__ void matrixMult(float *A, float *B, float *C, int n)
{
   int i = blockIdx.x*blockDim.x + threadIdx.x;
   int j = blockIdx.y*blockDim.y + threadIdx.y;


   
      C[i*n+j] = 0.0;       // C[i*n+j] = C[i][j]

      /* ---------------------------------
         Compute the matrix element
            Cij = ∑k=0..N-1 AikBkj 
         --------------------------------- */

        
  

}

 

The CUDA matrix multiplication algorithm - GPU part

The algorithm to compute C[i][j] is: 

__global__ void matrixMult(float *A, float *B, float *C, int n)
{
   int i = blockIdx.x*blockDim.x + threadIdx.x;
   int j = blockIdx.y*blockDim.y + threadIdx.y;


   
      C[i*n+j] = 0.0;       // C[i*n+j] = C[i][j]

      /* ---------------------------------
         Compute the matrix element
            Cij = ∑k=0..N-1 AikBkj 
         --------------------------------- */
      for ( int k = 0; k < n; k++ )
         C[i*n+j] += A[i*n+k] * B[k*n+j]; // C[i*n+j] = C[i][j]
  
}

Notice:   we created more than N2 threads with <<< B, T >>> !!!

The CUDA matrix multiplication algorithm - GPU part

To prevent the computation of non-existing matrix elements by the extra threads, we use: 

__global__ void matrixMult(float *A, float *B, float *C, int n)
{
   int i = blockIdx.x*blockDim.x + threadIdx.x;
   int j = blockIdx.y*blockDim.y + threadIdx.y;

   if ( i < n && j < n )
   {
      C[i*n+j] = 0.0;       // C[i*n+j] = C[i][j]

      /* ---------------------------------
         Compute the matrix element
            Cij = ∑k=0..N-1 AikBkj 
         --------------------------------- */
      for ( int k = 0; k < n; k++ )
         C[i*n+j] += A[i*n+k] * B[k*n+j]; // C[i*n+j] = C[i][j]
   }
}

DEMO: /home/cs355001/demo/CUDA/4-mult-matrix/2d-mult-matrix.cu

Postscript

  • Compare the execution time of the 2 CUDA programs that perform matrix multiplication: 

      mult-matrix2 1000 1024

       T = 1024 threads/thread block
       N*N = 1000000/T = 1024 = 976.562500 ---> using 977 blocks
       Elasped time = 113,536 micro secs
       #errors = 0

  2d-mult-matrix 1000 32 

       gridShape  = 32 x 32, # blocks  = 1024
       blockShape = 32 x 32, # threads = 1024
       Elasped time = 1,223,438 micro secs
       #errors = 0

  • Different grid shapes can result in:

    • Different access patterns of the matrix elements

    This will result in:

    • Different number of cache hits and different performance