- Fact:
- Some indexes (such as the B+-tree and index-sequential file) can be used to extract tuples of a relation in a sorted order
- Recall:
B+-tree
Notice that:
- Search keys in the
leaf nodes are
sorted
- We can use the record pointers to access the records in sorted order
- Search keys in the
leaf nodes are
sorted
- We will
usually
access the
sorted records of the
relation/file in a
random jumping-around manner:
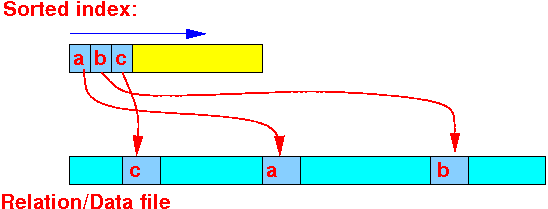
because the records may not be sorted in that order
- Unless
the index
is a clustering index
-
click here:
- The Phase 1
of the Join Algorithm based on
TPMMS
will
sort the
input relations:
(See:
click here)
- Phase 2 joins
the sorted relations:
- Requirement:
(for the zig-zag join algorithm):
- We want to
compute:
R(X,Y) ⋈ S(Y,Z)
- R has an sorted index on Y
- S has an sorted index on Y
- We want to
compute:
R(X,Y) ⋈ S(Y,Z)
- The zig-zag join algorithm:
while ( R ≠ empty and S ≠ empty ) do { Read the index of R with the smallest join key in buf(R):
Read the index of S with the smallest join key in buf(S):
if ( search keys are equal )
{
Use the index to access the tuples and join:
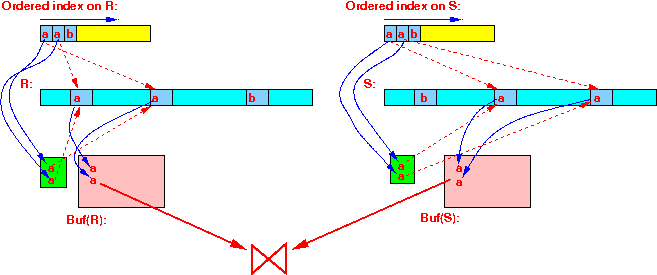Use next smallest value in indexes;
}
else
{
Remove the smallest value from the index;
}
}
- Example:
- Step 1:
1 ≠ 2 ⇒ move on
- Step 2:
3 ≠ 2 ⇒ move on
- Step 3:
3 ≠ 4 ⇒ move on
- Step 4:
4 == 4 ⇒ access tuples and join
- And so on
- Step 1:
- Notice that:
- The algorithm will
zig-zag through the
data files (relations) when
performing the
join:
Hence the name zig-zag join algorithm.....
- The algorithm will
zig-zag through the
data files (relations) when
performing the
join:
- Notice also that:
- The tuples themselves
are not accessed until
the index search keys
has found a
match
- No tuples are
accessed here:
Tuples are only accessed when there is a match at the index:
- The tuples themselves
are not accessed until
the index search keys
has found a
match
- The behavior of
the zig-zag algorithm is
very different using a
clustering index:
- The zig-zagging will be (almost) gone !!!
Graphically:
(It will not zigzag as long as the search key is the same, it only zig-zag when it moves from one serach key value to the next search key value)
- Consider the following
scenario 1:
relation R(X,Y) relation S(Y,Z) -------------------------------------------- B(R) = 1000 blks B(S) = 500 blocks T(R) = 10000 tuples T(S) = 5000 tuples R is clustered S is clustered No index on R Clustering sorted index on S V(S,Y) = 100
Available memory: M = 101 buffers
- One-pass Join Algorithm:
(See:
click here)
- Memory requirement:
M ≥ B(S) + 1 = 501
(See:
click here)
- Available memory: M = 101 ----- problem !!!
The one-pass Join algorithm is not applicable !!!
- Memory requirement:
M ≥ B(S) + 1 = 501
(See:
click here)
- 2-pass Join Algorithm based on
TPMMS
(See:
click here)
- Memory requirement:
M ≥ sqrt(B(R) + B(S))
= sqrt(1000 + 500) =
39
(See:
click here)
- Available memory: M = 101 ---- OK !!!
According to this webpage click here, the cost of (version 2) join algorithm based on TPMMS is:
# disk IOs = 3 B(R) + 3 B(S) // because R and S are clustered = 3 × 1000 + 3 × 500 = 4500 blocks
- Memory requirement:
M ≥ sqrt(B(R) + B(S))
= sqrt(1000 + 500) =
39
(See:
click here)
- The zig-zag join algorithm:
- Unfortunately, we
cannot
use the
zig-zag join algorithm:
- The input relations R and S must have an sorted index
- Since R does not have an index, we cannot use the zig-zag join algorithm....
However, we could adapt the zig-zag join...
- Unfortunately, we
cannot
use the
zig-zag join algorithm:
- Adapting
the zig-zag join algorithm
when one relation has
an sorted index:
- We sort the
relation R that
does not have an
index
- We can make use of the (sorted) index on S to scan S in a sorted manner
We proceed as follows:
- We must
sort
relation R
first --- because
we do not have a
sort index on R.
For simplicity (on calculation), we will use 100 buffers to sort R:
- We use 10 buffers to
read the
sorted chunks of
R
And use the remaining buffers to read S in a sorted manner using the clustering index on S:
Algorithm:
Find all tuples with the smallest join key value in the sorted chunks on R; Use the clustering index on S to find all tuples with the smallest join key value in S; Join these 2 set of tuples if possible;
Cost of this Join algorithm:
We need to scan all sorted chunks of R: we will use: B(R) disk I/Os Because the index on S is clustering, we will scan S once (will little skipping around): we will use: B(S) disk I/Os
# disk IO to join R and S = B(R) + B(S) blocks
Total cost of the Join algorithm:
First sort R and save sorted chunks on disk: 2 × B(R) Join sorted chunks of R and S, using clusting index: B(R) + B(S) Total cost = 3 B(R) + B(S) = 3 × 1000 + 500 = 3500 blocks (We beat TPMMS based join which has cost: 4500 block disk IOs)Note:
- We have assumed that the IO cost for the reading the index is negligible !!!
- We sort the
relation R that
does not have an
index
- Consider the following
scenario 2:
relation R(X,Y) relation S(Y,Z) -------------------------------------------- B(R) = 1000 blks B(S) = 500 blocks T(R) = 10000 tuples T(S) = 5000 tuples R is clustered S is clustered Clustering sorted index on R Clustering sorted index on S V(S,Y) = 100
Available memory: M = 101 buffers
- In this scenario, we can
apply the
zig-zag join algorithm
because:
- R has an (clustering) sorted index and
- S has an (clustering) sorted index
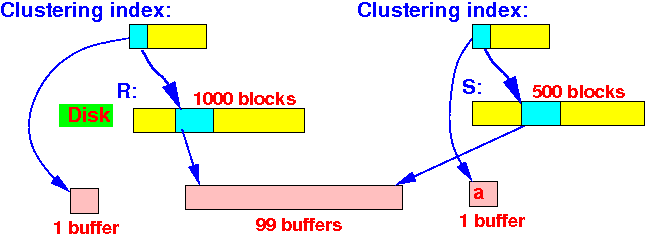
We use:
- 1 buffer to read the index of R
- 1 buffer to
read the
index of S
- The remaining (99) buffers
to hold
tuples with the
smallest join values from
R and S
- The performance of the
zig-zag join algorithm using
clustering indexes is:
Use the clustering index of R and scan R once we will use: B(R) disk I/Os (there is few skipping around because the index is clustering) Use the clustering index of S and scan S once we will use: B(S) disk I/Os (there is few skipping around because the index is clustering)
Total # disk IOs = B(R) + B(S) = 1000 + 500 = 1500 blocksNote:
- We have assumed that the IO cost for the reading the index is negligible !!!