- Floyd's modification on TCP (done in 1991) to achieve
constant increase in Throughput
has been improved by
Caini and Firrincieli in 2004
- This new TCP protocol is called:
TCP Hybla
- Although TCP Hybla has many
features in common with Floyd's work,
the design process of
TCP Hybla is much more careful and it is worth a study.
- Also, while Floyd only considered changing the operation of the TCP protocol to achieve constant (equal) increase in throughput in the congestion avoidance phase , Caini and Firrincieli also considered changing the operation of the TCP protocol to achieve constant (equal) increase in throughput in the slow start phase - as such, TCP Hybla is more "complete".
- The congestion window
W
is updated
per each NEW ACK
as follows:
- SS = Slow Start phase
- CA = Congestion Avoidance phase
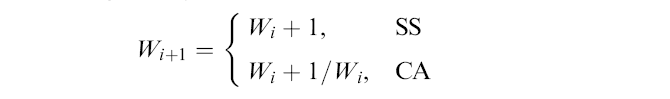
- SS = Slow Start phase
- As we know well by now, this results in:
- Doubling
of W
per RTT seconds during SS
- Increase of ONE in W per RTT seconds during CA
- Doubling
of W
per RTT seconds during SS
- We can express
W(t)
as followings:
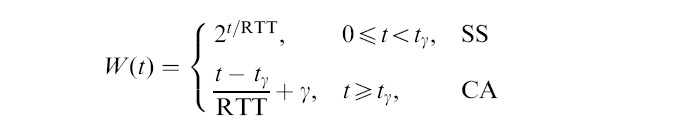
- The function
W(t)
clearly expressed these facts:
- At time t = 0 ,
W(0) = 20 = 1
- During SS,
at time t = RTT ,
W(RTT) = 21 = 2
- During SS,
at time t = 2*RTT ,
W(RTT) = 22 = 4
- So during SS, W(t)
doubles
per RTT seconds
Let γ be the value of the Slow Start Threshold (SSThresh)
Let t = tγ be the time when TCP exits SS (i.e., tγ = log(γ) because W(tγ) = 2tγ = γ )
- The second equation tells us that
at time
t = tγ ,
W(tγ) = γ
This is the moment that TCP exits SS and enters CA
- Then at time
t = tγ + RTT,
W(tγ + RTT)
= 1 + γ
So the second equation indeed increases congestion window W(t) by ONE per RTT seconds.
- At time t = 0 ,
W(0) = 20 = 1
- The following figure shows various functions
W(t)
for 3 TCP flows different values of RTT -
each TCP flow has the
same value of SS Threshold (32)
:
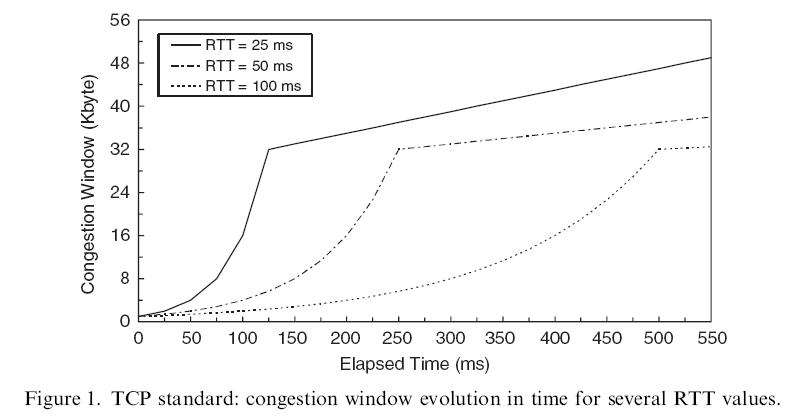
- We can clearly see that the
longer RTT
TCP flow took a
longer TIME
to
end the SLOW START phase
- In other words:
-
Even if we "take care of" the unfairness in
throughput
during the CA avoidance phase,
unfairness in throughput
will
still persist
because the TCP flows with longer RTT
will be
slower in the SLOW START phase
- From the function for the congestion window size
W(t) :
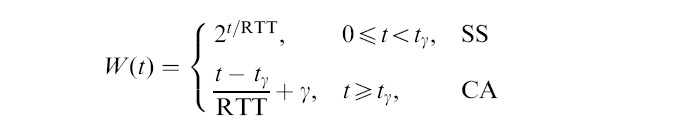
we can derive a simple function for the segment (packet) transmission rate of TCP:
RTT |<-------------------------------->| W(t) ---+----------------------------------+--------- \ \ W(t) segments en route to destination W(t) Transmission rate = B(t) = ------ (# packets / sec) RTT
- The throughput
is then the
area under the function B(t)
(which is equal to the
integral of B(t)):
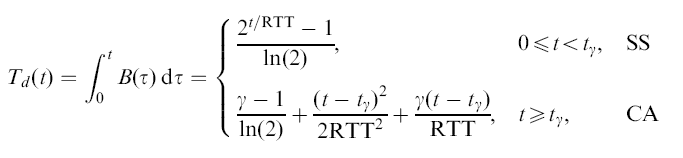
(This situation is similar to the example in Physics:)
- velocity = amount of distance traveled per sec
- distance = area under the velocity function
- In order to make the
throughput
of TCP
independent
of
RTT , we must do the following:
- throughput
during the SS phase must be
independent
of
RTT
- throughput during the CA phase must be independent of RTT
- throughput
during the SS phase must be
independent
of
RTT
- Consider the following
normalized round trip time ρ:
RTT ρ = ------ RTT0where RTT0 is some pre-determined round trip time (e.g., 25 msec).
- In order to make
ALL TCP Hybla connection
go through the
SAME duration of slow start
for a given SS Thrshold value
γ,
the TCP Hybla
Slow Start threshold value
is changed to:
Reno Slow Start threshold value = γ RTT TCP Hybla Slow Start threshold value = ρ * γ = ------ γ RTT0
- Let us first give the
TCP Hybla
congestion window function as is
(later we will determine
how to increase CWND
to achieve this function):
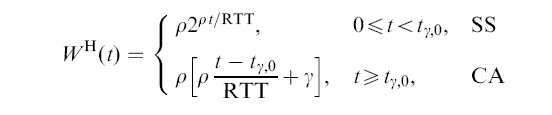
where
- ρ * γ
is the TCP Hybla
Slow Start threshold value
- tγ,0 is the time that TCP Hybla exits the Slow Start phase (and enters the congestion avoidance phase)
- ρ * γ
is the TCP Hybla
Slow Start threshold value
- If we re-write
WH(t)
without using
ρ ,
some computations are simplified:
RTT ρ 2(ρ*t/RTT) = ----- 2(t/RTT0) . . . . . . . . (SS) RTT0 WH(t) = t - tγ,0 RTT t - tγ,0 ρ ( ρ ---------- + γ ) = ----- ( --------- + γ ) . . . . (CA) RTT RTT0 RTT0
- The
TCP Hybla
congestion window function has the following properties:
- TCP connection with the
SS Threshold
will take the
same amount of time
to
exit
the SS phase
Reason:
- Suppose the SS Threshold is
γ
- Then TCP Hybla will use this value to terminate
the SS phase:
ρ * γ
- Therefore, the time
tγ,0
that a TCP Hybla
agent
exit
the SS phase
is equal to:
RTT WH(t) = ----- 2(t/RTT0) = ρ * γ RTT0
RTT RTT ==> ----- 2(t/RTT0) = ------ * γ RTT0 RTT0
<==> 2(t/RTT0) = γ
t <==> ----- = log2( γ ) RTT0
<==> t = RTT0 log2( γ )
==> tγ,0 = RTT0 log2( γ ) - Since tγ,0 is independent of RTT, every TCP Hybla connection will take the same amount of time to exit the SS Phase for the same SS Threshold
- Suppose the SS Threshold is
γ
- The
segment transmission rate
function of TCP Hybla is
independent from RTT:
1 = ----- 2(t/RTT0) . . . . . (SS) RTT0 WH(t) BH(t) = ----- RTT 1 t - tγ,0 = ----- ( --------- + γ ) . . . . (CA) RTT0 RTT0As we have just seen before, tγ,0 is independent of RTT
Therefore, RTT does not appear anywhere as a factor in BH(t) --- so BH(t) is independent of RTT
- TCP connection with the
SS Threshold
will take the
same amount of time
to
exit
the SS phase
- The following are some plots of 3 different
TCP Hybla congestion window functions
for different value of RTT
with the
SAME SS Threshold:
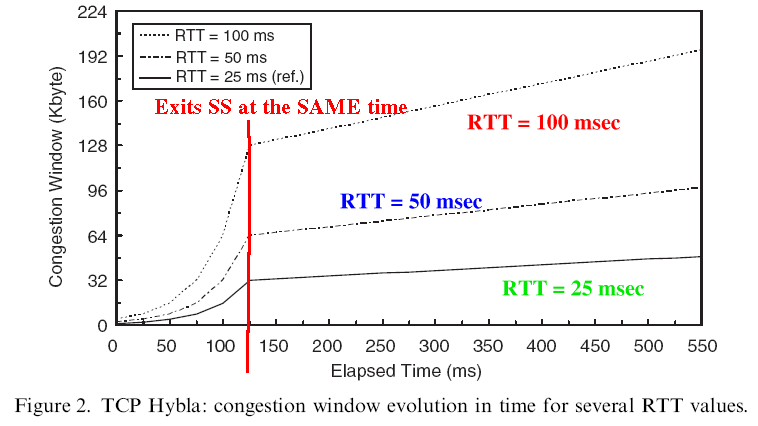
- Notice that all TCP Hybla connection will
exit
the >Slow Start Phase at the same time
- However,
the congestion window at the exit time
is &rho * γ
A TCP Hybla connection with longer RTT needs to end up at a higher CWND to achieve the SAME throughput per time unit (second)
- This is a simple matter of exercise
(in Analysis 101 - integration theory) to show that
the TCP Hybla
throughput function
is equal to:
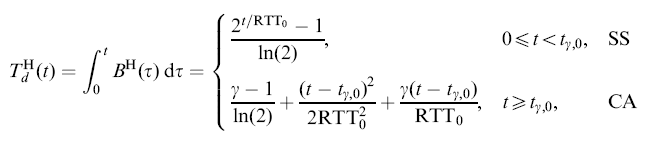
- OK, we know that we want the
congestion window function
to be:
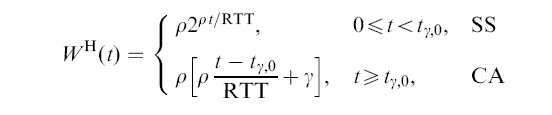
Now HOW should the CWND be updated ( per each NEW ACK) so that TCP Hybla's CWND will be equal to the given function ?
- In other words:
What are the values for α and β for the update of CWND W:
WHi + α . . . . (SS) WHi+1 = WHi + β . . . . (CA)
so that:
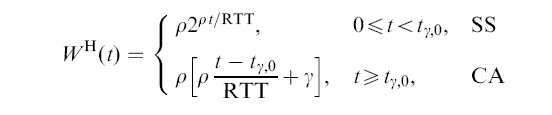
- According to the authors of TCP Hybla, the
CWND window update must be as follows:
WHi + 2ρ - 1 . . . . (SS) WHi+1 = ρ2 WHi + ----- . . . . (CA) WHiWe won't try to derive it, we will just verify it (it's a lot easier to verify the correctness of a solution than to find a solution)
- Decrease algorithm:
- The descrease algorithm is the same as TCP Reno
- Except that after obtaining:
-
SSThreashold = CWND / 2
TCP Hybla will only exit the SS phase after CWDN > ρ * SSThreashold
- The descrease algorithm is the same as TCP Reno
SS Phase
- The TCP Hybla congestion window function is:
WH(t) = ρ 2(ρ*t/RTT)
Some key values: WH(0*RTT) = ρ 2(0*ρ) WH(1*RTT) = ρ 2(1*ρ) WH(2*RTT) = ρ 2(2*ρ) WH(3*RTT) = ρ 2(3*ρ) ρ * 20ρ ρ * 21ρ ρ * 22ρ ρ * 23ρ +---------------+---------------+---------------+---------------+ 0 RTT 2RTT 3RTT 4RTT | ^ | ^ | ^ | ^ | | | | | | | | V | V | V | V | 1 packet 2 packets 4 packets 8 packets (1) (3) (7) (15) - The CWND increase algorithm during SS phase is given
by:
WHi+1 = WHi + 2ρ - 1 . . . . (SS) WH1 = ρ
Maple Solution: > rsolve( {w(n) = w(n-1) + 2^rho - 1, w(1) = rho}, w(k)); rho rho rho + 2 - 2 2 + (-1 + 2 ) (k + 1) > simplify(%); rho rho rho + 1 - 2 - k + 2 k > g := unapply(%, k); rho rho g := k -> rho + 1 - 2 - k + 2 k
> g(rho); rho rho 1 - 2 + 2 rho > g(rho + g(rho)); rho rho rho 2 - 4 + 4 rho > g(rho + g(rho)+g(rho + g(rho)) ); rho rho rho 4 - 8 + rho 8
Some key values: WH1 = ρ WRTT = ρ + g(ρ) +------------------+------------------+------------------+------------------+ 0 RTT 2RTT 3RTT 4RTT | ^ | ^ | ^ | ^ | | | | | | | | V | V | V | V | ρ packet WRTT packets g(ρ) g(ρ + g(ρ)) ρ ρ g(ρ) = 1 - 2 + ρ 2 ρ ρ ρ g(ρ + g(ρ)) = 2 - 4 + ρ 4 ρ ρ ρ g(ρ + g(ρ) + g(ρ + g(ρ)) = 4 - 8 + ρ 8
The windows at the whole RTT time is approximately: ρ WRTT ~= ρ 2 ρ 2ρ W2RTT ~= ρ 4 = ρ 2 ρ 3ρ W2RTT ~= ρ 8 = ρ 2 - You can verify the CA case in a homework.
- Here is the throughput of 3 flows using
TCP Hybla and 3 flows using TCP Reno
with
different RTT values:
- As we know, the TCP Reno
flows have different throughputs
- Amazingly, ALL TCP Hybla have the (approximately) SAME throughput
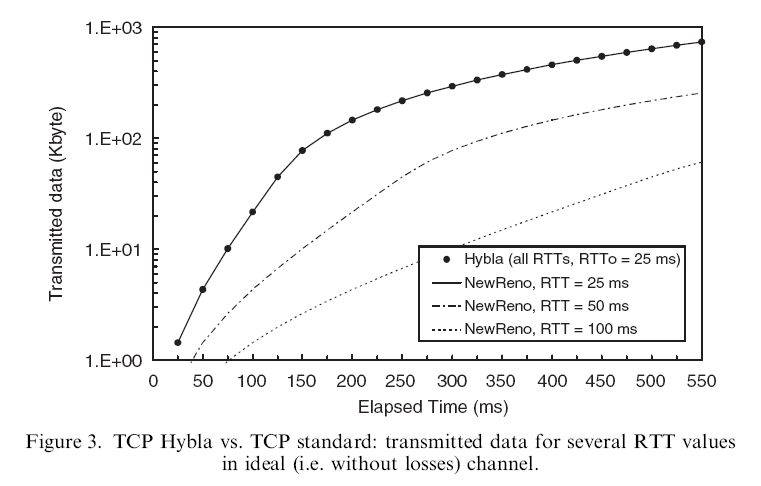
- As we know, the TCP Reno
flows have different throughputs
- TCP Hybla is
NOT incorporated
in NS
- But, you can added it easily to NS by
following the following instructions.
- TCP Hybla Source code:
(Demo above code)

- TCP Hybla C++ header file: click here
- TCP Hybla C++ program file: click here
- Instructions to incorporate TCP Hybla into NS: click here