- Strength:
- Achieves same rate of increase in TCP throughput that is independent of RTT
Short-coming:
- Floyd's method is
only valid
during the
congestion avoidance phase ,
- The rate of increase in TCP throughput is not equal during the slow start phase
- Net effect:
- Floyd's "constant-increase" TCP method
does not achieve
equal TCP throughput
among TCP flows
with different RTTs
- Because:
- During slow start phase,
the shorter RTT
TCP flows will
acquire a larger CWND
- These shorter RTT TCP flows will retain their CWND "advantage" in the congestion avoidance phase
- During slow start phase,
the shorter RTT
TCP flows will
acquire a larger CWND
- Example:
how RTT will affect
the TCP protocol in the
slow start phase
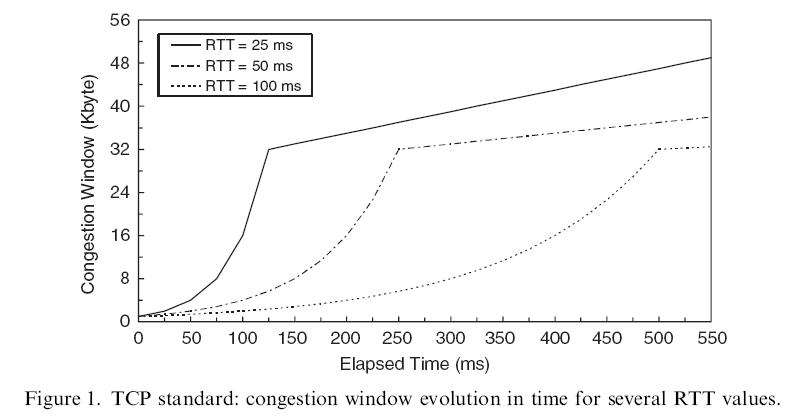
Notes:
- 3 TCP flows with
SSThresh = 32
TCP flows have different RTTs
- A larger RTT will
make a TCP flow
stay longer
in the slow start phase
- TCP flows with
smaller RTT will
gain a "CWND advantage"
over
TCP flowswith
larger RTT
The advantage is retained during congestion avoidance when Floyd's method is deployed
- 3 TCP flows with
SSThresh = 32
- Floyd's "constant-increase" TCP method
does not achieve
equal TCP throughput
among TCP flows
with different RTTs
- TCP Reno
CWND update algorithm:
- Update W (CWND
for each
new ACK
as follows:
- SS = Slow Start phase
- CA = Congestion Avoidance phase
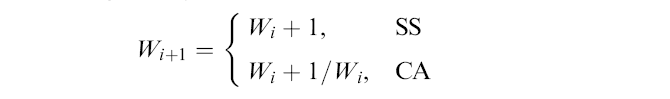
- SS = Slow Start phase
- Update W (CWND
for each
new ACK
as follows:
- The CWND update algorithm
will achieve:
- During
SS (slow start) phase:
- CWND = 2 × CWND after every RTT seconds
In other words:
CWND = 1 when t = 0 CWND = 2 when t = RTT CWND = 4 when t = 2*RTT CWND = 8 when t = 4*RTT .... CWND(t) = 2t/RTT ......... (1)
- Suppose:
- TCP
exits the
slow start (SS) phase at time
tγ
- The CWND at
exit time
tγ =
γ
I.e.: CWND(tγ) = γ
- TCP
exits the
slow start (SS) phase at time
tγ
- During
CA (congestion avoidance)
phase:
- CWND = CWND + 1 after every RTT seconds
In other words:
CWND = γ when t = tγ CWND = γ + 1 when t = tγ + RTT CWND = γ + 2 when t = tγ + 2*RTT CWND = γ + 3 when t = tγ + 3*RTT ... CWND(t) = γ + (t − tγ)/RTT ......... (2)
- During
SS (slow start) phase:
- We can express
CWND (W)
as a function of time t
(W(t))
as follows:
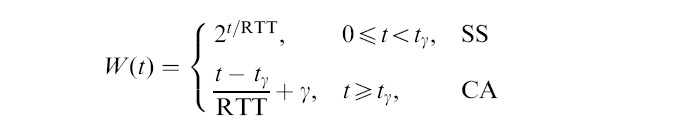
- γ
= the value of the
Slow Start Threshold (SSThresh)
- tγ = the time when TCP exits the Slow Start phase
- γ
= the value of the
Slow Start Threshold (SSThresh)
- The value of
tγ
can be found by solving
this equation:
W(tγ) = γ tγ ----- RTT ==> 2 = γ tγ <==> ----- = log2(γ) RTT <==> tγ = RTT × log2(γ)
- For highlight purpose:
- γ = 2tγ/RTT
............(3)
- tγ = RTT *log(γ) ............(4)
- γ = 2tγ/RTT
............(3)
- Segment transmission rate B(t)
- B(t) = number of segments (packets) transmitted by TCP per second
- Relationship between B(t) and
CWND W(t):
RTT sec |<-------------------------------->| W(t) packets ---+----------------------------------+--------- \ / (ACKs) \ / W(t) segments en route to destination
# packets transmitted in RTT sec = W(t) Therefore: W(t) B(t) = ----- (# packets / sec) RTT - Note:
- B(t)
in the TCP Hybla paper
means:
"segment transmission rate
at time t"
- In contrast:
B(t)
in Padhye's paper means:
"Throughput of TCP at time t"
- Again, I keep the notation used in each paper
- B(t)
in the TCP Hybla paper
means:
"segment transmission rate
at time t"
- TCP Throughput is equal to the
area under the graph of B(t):
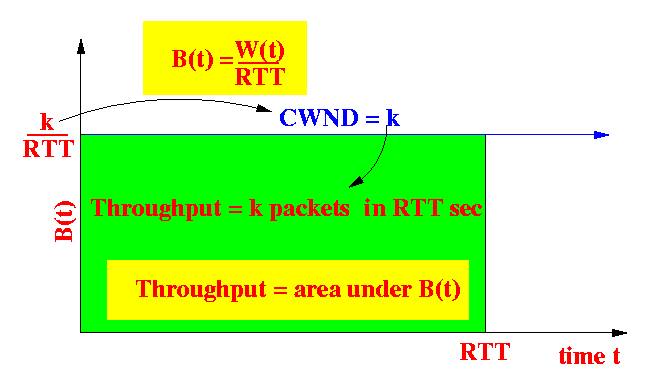
- In Mathemetical terms:

- To design a
"equal" throughput
TCP protocol
that can achieve the
same throughput
over
the slow start
and
the
congestion avoidance
phases,
we must first
- Find a throughput expression for TCP over both the slow start and the congestion avoidance phases
(We don't need to be very precise, we only need a ball park figure)
- The
congestion window size W (CWND)
varies in time according
the the function
W(t) :
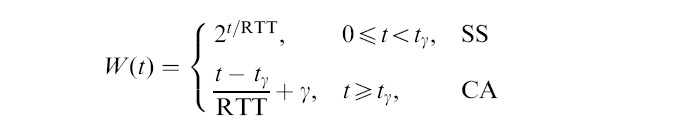
- The throughput T(t)
at time t
of the TCP connection
is equal to:
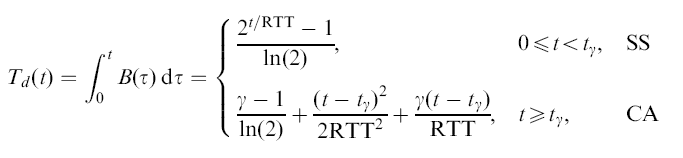
- We can verify
these reuslts with Maple:
W(t) B(t) = ------ RTT
Slow Start phase: ============================== W(t) = 2t/RTT for t < tγ 0∫t B(t) dt = 0∫t ( 2x/RTT/RTT ) dxComputing: 0∫t ( 2x/RTT/RTT ) dx Maple: T := t -> integrate( (2^(x/RTT))/RTT, x=0..t); / t \ |---| \RTT/ -1 + 2 ----------- ln(2)
TCP switches over to Congestion Avoidance at t = tγ / tγ\ |---| \RTT/ -1 + 2 T(tγ) = ----------- ....... (5) ln(2) From: γ = 2tγ/RTT ...... (3) We have: -1 + γ T(tγ) = ----------- ...... (6) ln(2)
Congestion Avoidance phase: ============================== t - tγ W(t) = ------- + γ for t ≥ tγ RTT t - tγ γ B(t) = ------- + ------ for t ≥ tγ RTT2 RTT 0∫t B(t) dt = 0∫tγ B(t) dt + tγ∫t B(t) dt (Use Eq. (6)) = T(tγ) + tγ∫t B(t) dt -1 + γ = --------- + tγ∫t B(t) dt ln(2) -1 + γ = --------- + tγ∫t { [(t - tγ)/RTT2] + γ/RTT } dt ln(2)Computing: tγ∫t { [(t - tγ)/RTT2] + γ/RTT } dt: Maple: integrate( (x-t0)/(RTT^2) + Gamma/RTT, x=t0..t); 2 2 t - t0 t0 (t - t0) Gamma (t - t0) -------- - ----------- + -------------- 2 2 RTT 2 RTT RTT
(This relationship between T(t) and W(t) is similar to the relationship between velocity and distance traveled:)
- velocity = amount of distance traveled per sec
- distance = area under the velocity function
- In order to make the
throughput
of TCP
independent
of
RTT ,
we require that:
- TCP throughput
during the CA phase
must be
independent
of
RTT
(Floyd's algorihm can achieve this already)
- Also:
TCP throughput
during the SS phase must be
independent
of
RTT
(This is the contribution of TCP Hybla)
- TCP throughput
during the CA phase
must be
independent
of
RTT
- Definition: Normalized RTT ρ
RTT ρ = ------ RTT0where RTT0 is some pre-determined round trip time (e.g., 25 msec).
- We have to re-write the TCP window function in term of ρ first....
- Recall: TCP Reno's slow start
- CWND = 1 (packet)
- TCP Hybla's initial slow start window:
- CWND = ρ (packet)
- Suppose we want to
achieve the following
Window increase function:
(don't ask me how the authors come up with this function :-), we will see that it works....)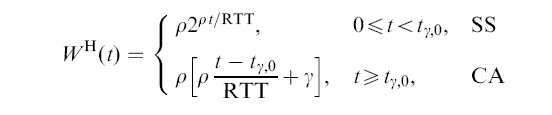
where
- ρ * γ
= the TCP Hybla's
Slow Start threshold value
- tγ,0
= the time that
TCP Hybla
exits the
Slow Start phase
(and enters the congestion avoidance phase)
WH(tγ,0) = ρ × γ ==> ρ × 2ρtγ,0/RTT = ρ × γ <==> 2ρtγ,0/RTT = γ <==> ρtγ,0/RTT = log2(γ) RTT <==> tγ,0 = log2(γ) × ----- ρ <==> tγ,0 = log2(γ) × RTT0 ......... (7)
- ρ * γ
= the TCP Hybla's
Slow Start threshold value
- We can re-write
WH(t)
to remove the symbol
ρ
to
simplify computation:
+-- | RTT | ρ 2(ρ*t/RTT) = ----- 2(t/RTT0) . . . . . . . . (SS) | RTT0 | WH(t) = | | | t - tγ,0 RTT t - tγ,0 | ρ ( ρ ---------- + γ ) = ----- ( --------- + γ ) . . . . (CA) | RTT RTT0 RTT0 +-- - NOTE:
- Notice that the congestion window CWND must increase faster when RTT is larger to compensate for the slowness in updating CWND
- The TCP Hybla protocol
has the following properties:
- The
segment (packet) transmission rate
function
BH(t)
of TCP Hybla is
always
independent from RTT:
+-- | 1 | = ----- 2(t/RTT0) . . . . . (SS) | RTT0 | WH(t) | BH(t) = ----- | RTT | | | 1 t - tγ,0 | = ----- ( --------- + γ ) . . . . (CA) | RTT0 RTT0 +--As we have just seen before:
tγ,0 = log2(γ) × RTT0 ......... (7)tγ,0 is independent of RTT
- Since RTT does not appear in BH(t) , the function BH(t) is independent of RTT
- Hybla TCP connections that have the
same SS Threshold
will
exit the SS phase
at the
same time
Reason:
- Suppose a Hybla TCP connection
has the SS Threshold =
γ
- Then Hybla TCP connection
exits
the SS phase at time:
tγ,0 = log2(γ) × RTT0 ......... (7)
- Since tγ,0 is independent of RTT, every TCP Hybla connection will exit the SS Phase at the same time !!!!
Example:
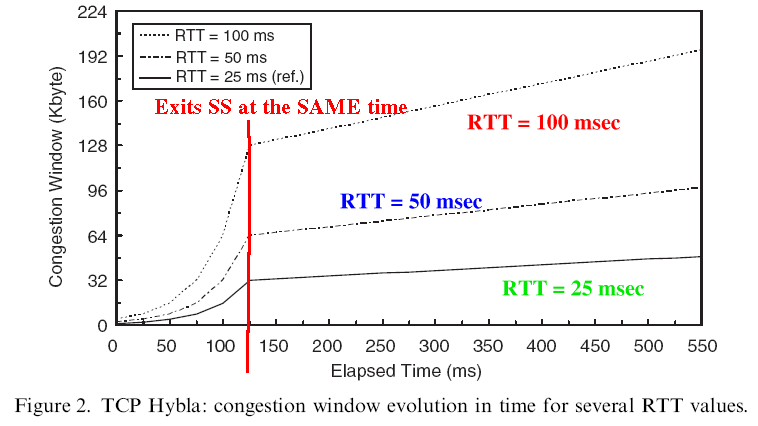
Note:
- TCP connections have
different RTTs
- All TCP connections
exit the
Slow Start phase
at the same time (approximately)
- Note that
a TCP connection with
a larger RTT
has a larger CWND
This is necessary to compensate for the larger RTT to obtain an equal transmission rate
- Suppose a Hybla TCP connection
has the SS Threshold =
γ
- The
segment (packet) transmission rate
function
BH(t)
of TCP Hybla is
always
independent from RTT:
- Result of these 2 properties:
- Throughput of TCP Hybla is independent of RTT
- The TCP Hybla
segment (packet)
transmission rate function
BH(t)
was given by:
+-- | 1 | = ----- 2(t/RTT0) . . . . . (SS) | RTT0 | WH(t) | BH(t) = ----- | RTT | | | 1 t - tγ,0 | = ----- ( --------- + γ ) . . . . (CA) | RTT0 RTT0 +--
- We can obtain the
TCP Hybla
throughput function TH(t)
by
integrating BH(t):
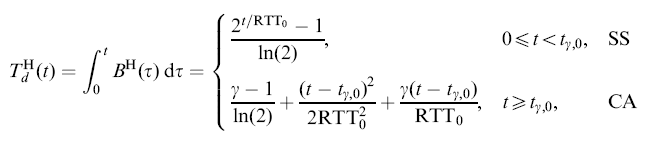
You can see that the throughput function of Hybla TCP is INDEPENDENT of RTT
- OK, we see that
TCP Hybla
has the
properties that are
neccesary to
design an
RTT-independent TCP
- $64,000 questions:
-
How do we update CWND
so that the CWND
matches
the
TCP Hybla
congestion window function
BH(t):
+-- | 1 | = ----- 2(t/RTT0) . . . . . (SS) | RTT0 | WH(t) | BH(t) = ----- | RTT | | | 1 t - tγ,0 | = ----- ( --------- + γ ) . . . . (CA) | RTT0 RTT0 +--
-
How do we update CWND
so that the CWND
matches
the
TCP Hybla
congestion window function
BH(t):
- A TCP congestion control
mechanism consists of 2 parts:
- Increase mechanism
(when TCP receives
a new ACK)
- Decrease mechanism (when TCP detects a time out or 3 duplicate ACKs)
- Increase mechanism
(when TCP receives
a new ACK)
- Consider the following
general update mechanism:
+-- | WHi + α . . . . (during SS) | WHi+1 = | | | WHi + β . . . . (during CA) +--such that:
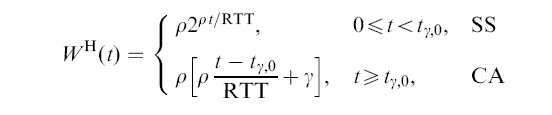
- According to the
authors of TCP Hybla, the
CWND window update mechanism is as follows:
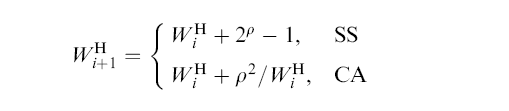
I.e.: +-- | WHi + 2ρ - 1 . . . . (SS) | WHi+1 = | | ρ2 | WHi + ----- . . . . (CA) | WHi +--with WH0 = ρ (initial CWND at slow start)
In a homework, you can verify this fact
(it's a lot easier to verify the correctness of a solution than to find a solution)
- Note:
- The authors
did not specify
carefully
how CWND must be decreased
- I tried my best to look
for clue in the paper
and in their program source code.
- The only clue I can find
in their paper
is:

- The following on the decrease algorithm are the best to my knowledge...
- The authors
did not specify
carefully
how CWND must be decreased
- Decrease algorithm:
- When TCP detects
a timeout
(i.e. Slow Start )
- SSThreshold = ρ * CWND/2
This is according to:

- CWND = ρ * 1
Note:
- I was able to verify this.
- I found this statement:
- wnd_init_ = (int)floor(rho_);
They then call TcpAgent::timeout(tno); which will use wnd_init_ as initial cwnd_
See: click here - look for the function void HyblaSTcpAgent::timeout(int tno)
- I was able to verify this.
- SSThreshold = ρ * CWND/2
- Fast Recovery (Triple Duplicate ACK)
- SSThreashold = CWND/2
- CWND = CWND/2
That's my guess because I found this statement in the source code:
- slowdown( CLOSE_SSTHRESH_HALF | CLOSE_CWND_HALF );
- SSThreashold = CWND/2
- When TCP detects
a timeout
(i.e. Slow Start )
- Here is the throughput of 3 flows using
TCP Hybla and 3 flows using TCP Reno
with
different RTT values:
- As we know, the TCP Reno
flows have different throughputs
- Amazingly, ALL TCP Hybla have the (approximately) SAME throughput
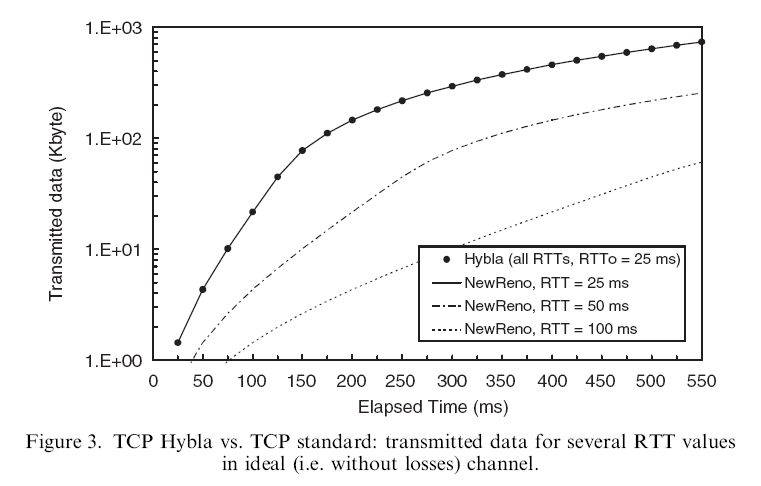
- As we know, the TCP Reno
flows have different throughputs
- TCP Hybla is
NOT incorporated
in NS
- But, you can added it easily to NS by
following the following instructions.
- TCP Hybla Source code:
(Demo above code)

- TCP Hybla C++ header file: click here
- TCP Hybla C++ program file: click here
- Instructions to incorporate TCP Hybla into NS: click here