Notations:
- S
= source node (the node performing the computation)
- N
= set of all nodes that have reported a link state message
(this is normally all nodes in the network, unless there are catastrophic network failures) - ReachSet
= set of nodes that are reached with minimum cost
- d(S, n) = current minimum distance from S to node n
Dijsktra's Algorithm:
(Initialization step)
ReachSet := {S} (S is the node that performs the computation)
(Currently, only node S canbe reach from S)
for each node n in N - {S} do
{
d(S,n) := linkcost(S,n);
directionTo(n) := n;
}
|
-
Consider the following network:
- Red links:
known (discovered) nodes
(but not certain how to get their with least cost)
- Blue links:
known (discovered) nodes
with KNOWN least cost path
- Black links: undiscovered nodes
- We know the best way from B to C to directly to C
- We have discovered a new way to get to D with better cost
- End result: Routing table of B
Destination | Next Hop ----------------+----------------- A | A B | - C | C D | C E | C
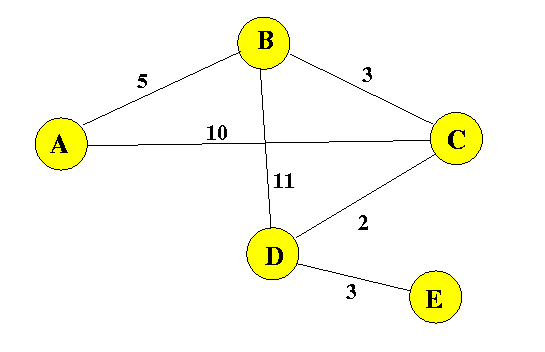
The corresponding matrix representation (distance matrix) is as follows:
Distance matrix
To:
From A B C D E
------+---------------------------------
A | * 5 10 * *
B | 5 * 3 11 *
C | 10 3 * 2 *
D | * 11 2 * 3
E | * * * 3 *
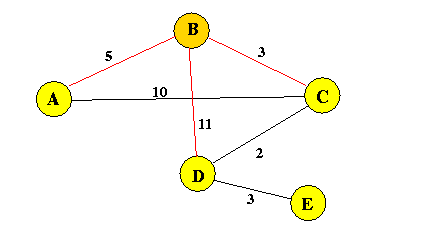
The computation of the shortest path from source node B proceeds as follows:
(Initialization step)
ReachSet := {B}
d(B,A) = 5; directionTo(A) = A;
d(B,C) = 3; directionTo(C) = C;
d(B,D) = 11; directionTo(D) = D;
d(B,E) = *; (= infinite) directionTo(E) = E;
Current Situation::
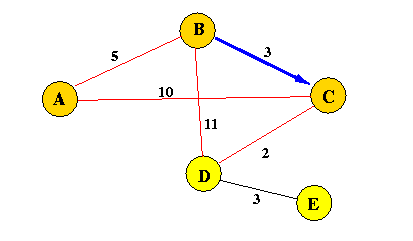
Iteration 1:
d(B,C) = 3; is smallest among the unreached nodes
m = C; (Node C is added to the ReachSet - we now know how
to get to C with the shortest possible path)
We must now update the state variables....
ReachSet := {B, C};
d(B,A) = min( 5, 3 + 10); = 5; directionTo(A) = A;
d(B,D) = min( 11, 3 + 2) = 5; directionTo(D) = C;
d(B,E) = min( *, 3 + * ); = * directionTo(E) = E;
Current Situation::
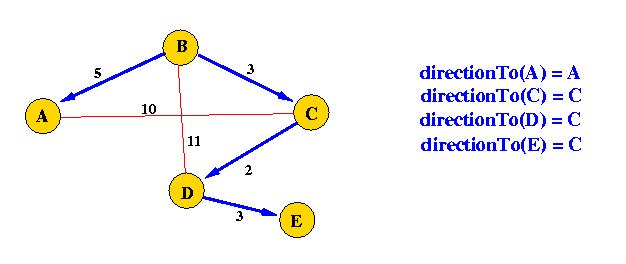
Iteration 2:
d(B,A) = 5; is smallest among the unreached nodes
m = A; (Node A is added to the ReachSet - we now know how
to get to A with the shortest possible path)
We must now update the state variables....
ReachSet := {A, B, C};
d(B,D) = min( 5, 5 + *) = 5; directionTo(D) = C;
d(B,E) = min( *, 5 + * ); = * directionTo(E) = E;
Current Situation::
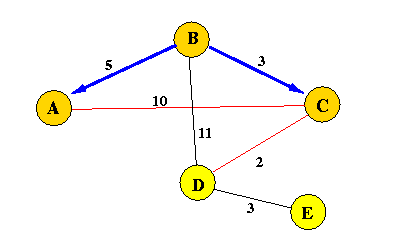
Iteration 3:
d(B,D) = 5; is smallest among the unreached nodes
m = D;
ReachSet := {A, B, C, D};
d(B,E) = min( *, 5 + 3 ); = 8 directionTo(E) = C;
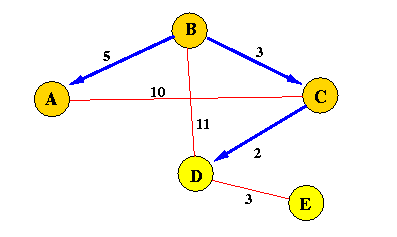
Iteration 4:
d(B,E) = 8; is smallest among the unreached nodes
m = E;
ReachSet := {A, B, C, D, E};
ReachSet == N, DONE...
Current Situation::