Notations:
- S = source node (the node performing the computation)
- N = set of all nodes that have reported a link state message
(this is normally all nodes in the network, unless there are catastrophic network failures) - ReachSet = set of nodes that are reached with minimum cost
- d(S, n) = current minimum distance from S to node n
(Initialization step)
ReachSet := {S} (S is the node that performs the computation)
for each node n in N - {S} do
{
d(S,n) := linkcost(S.n);
directionTo(n) := n;
}
(Actual algorithm)
while ( ReachSet != N ) do
{
(Inclusion step)
Find the node m in N - ReachSet that has min. value for d(S,m)
ReachSet := ReachSet + {m}
(Update step)
for each node n in N - ReachSet do
{
d(S,n) = min( d(S,n), d(S,m)+linkcost(m,n) )
if ( d(S,m)+linkcost(m,n) < d(S,n) )
directionTo(n) := directionTo(m);
}
}
|
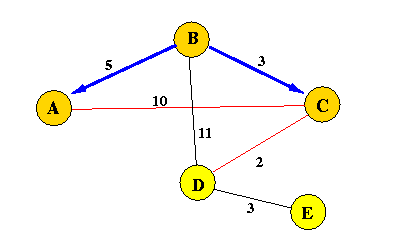
Consider the following network:
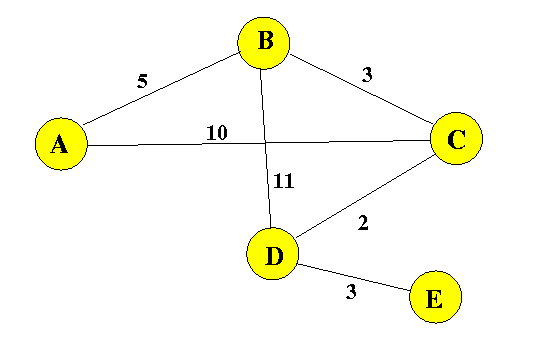
The corresponding matrix representation (distance matrix) is as follows:
Distance matrix
To:
From A B C D E
------+---------------------------------
A | * 5 10 * *
B | 5 * 3 11 *
C | 10 3 * 2 *
D | * 11 2 * 3
E | * * * 3 *
The computation of the shortest path from source node B proceeds as follows:
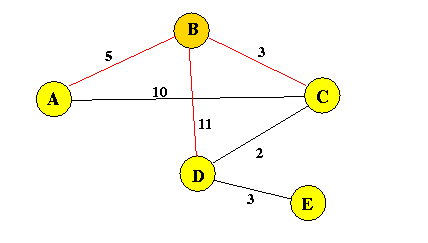
(Initialization step)
ReachSet := {B}
d(B,A) = 5; directionTo(A) = A;
d(B,C) = 3; directionTo(C) = C;
d(B,D) = 11; directionTo(D) = D;
d(B,E) = *; (= infinite) directionTo(E) = E;
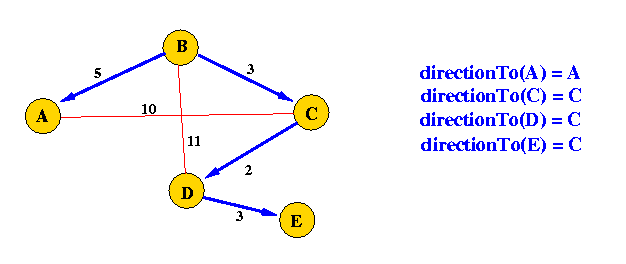
Iteration 1:
m = C;
ReachSet := {B, C};
d(B,A) = min( 5, 3 + 10); = 5; directionTo(A) = A;
d(B,D) = min( 11, 3 + 2) = 5; directionTo(D) = C;
d(B,E) = min( *, 3 + * ); = * directionTo(E) = E;
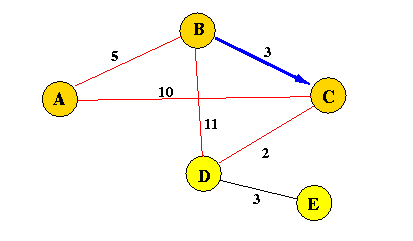
Iteration 2:
m = A;
ReachSet := {A, B, C};
d(B,D) = min( 5, 5 + *) = 5; directionTo(D) = C;
d(B,E) = min( *, 5 + * ); = * directionTo(E) = E;
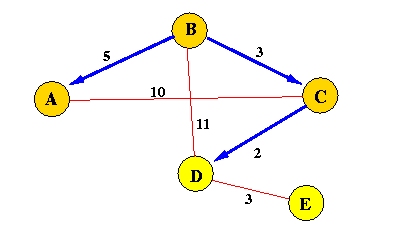
Iteration 3:
m = D;
ReachSet := {A, B, C, D};
d(B,E) = min( *, 5 + 3 ); = 8 directionTo(E) = C;
Iteration 4:
m = E;
ReachSet := {A, B, C, D, E};
ReachSet == N, DONE...