---

Distance Vector Routing Algorithm (Distributed)

---

• The Distance Vector Routing Algorithm is also known as the Distributed Bellman-Ford algorithm, because the update procedure is the algorithm for finding the shortest path developed by Bellman and Ford.

• Documentation on Distance Vector protocols can be found in Internet RFC 1058: click here

  Best known example of Distance Vector Routing Algorithm is:

  • Routing Information Protocol (RIP) [bundled with Berkeley's UNIX distribution]

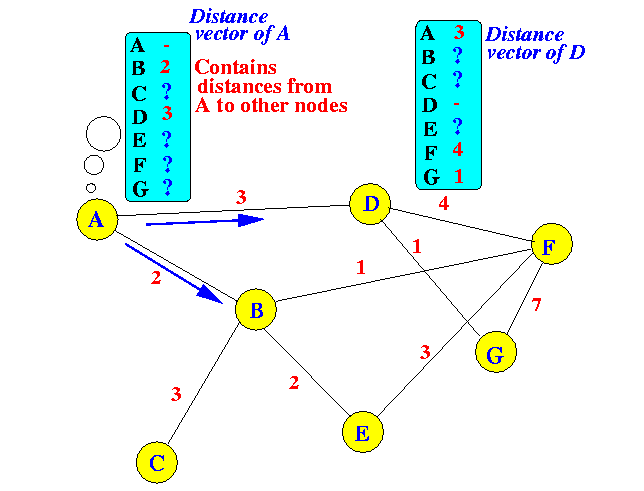
• Recall that in distance vector type route computation algorithm, a node sends its distance vector to all nodes to only its neighbor nodes of the network.

  Unlike the link state type algorithms, nodes in distance vector type algorithms must exchange many rounds of messages.

• Structure of the distance vector messages

  • First, let's look at the content of the messages that nodes send to each other:

    

    The content of the messages are of the form:

        (SrcNode)
        ToNode1   Distance1
        ToNode2   Distance2
        ToNode3   Distance3
        ....
    

    The meaning of (ToNode1, Distance1) is: "the distance from node "SrcNode" to the destination node "ToNode1" is "Distance1"...

• Data Structures using in Routers:
  • Each node (router) maintains two data structures:
    • a routing table (this data structure is the same as the one discussed before.... every router must have one to perform routing)

    • a distance table (this data structure is new)

    The structures of the distance table is given in the following figure (in the pinkish box):

    

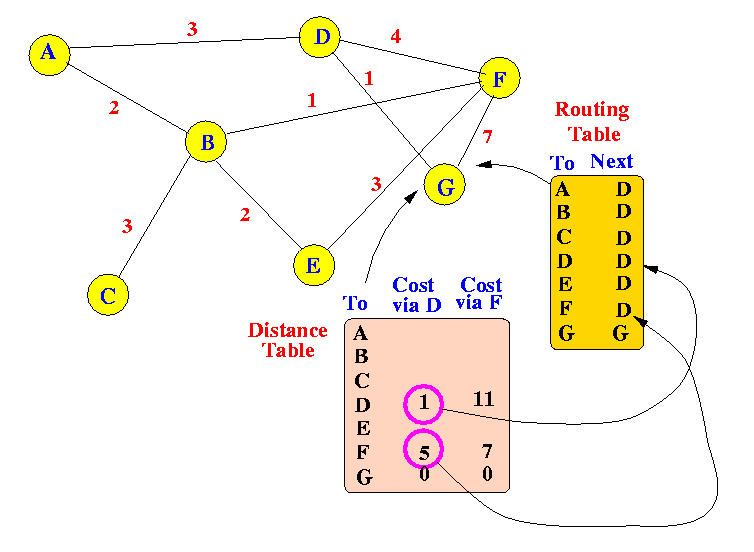
    • The first column (labeled with "To") contains the identity of each node in the network - this the "key" which the other values are indexed on.

    • The remaining columns in the distance table are distance information to each destination through a neighboring node

      If a node is connected to $k$ neighbor nodes, then its distance table will have $k$ columns (besides the first column).

    • The value under a neighbor node column in the distance table is the cost (delay) from yourself to the destination if you would send a packet to its destination by sending it first to that neighbor node .

      OK, I know this is a mouthful, so let me illustrate it with a concrete example. Consider this network:

      

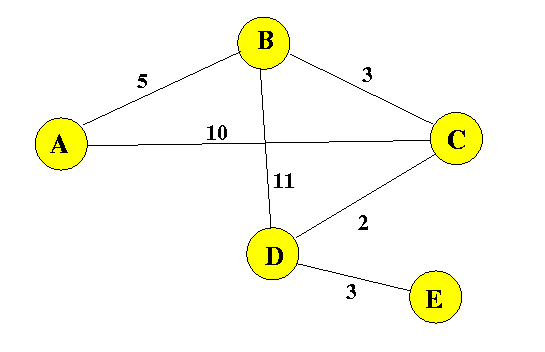
      Node D has 3 neighbors: B, C, E. So D's distance table will have 3 columns. Here are some values in the table:

      Distance table for node D:
      
         To    Via B   Via C   Via E
       ------+-------+-------+-------
         A
         B
         C			   7   <--- D send to E via C with cost 7
         D
         E                       3   <--- D send to E via E with cost 3
      

    Clearly, the cost for D to send a message to E is 3... (just read it right from the network)

    Now, it is less intuitive to compute the cost for D to send a message to E when D send it first to C... (it is not "natural"). What will C do with such a message ? Answer: send it to D... And D will then send it to E. So... the cost for D to send a message to E by sending it first to C is: 2 + 2 + 3 = 7. And that is why:

• The update procedure (Bellman & Ford) :
  • A node will (from time to time) receive distance vector messages from a neighbor node

  • When it receives a distance vector message, the node re-calculates the distance table using the following procedure:

    for each entry (ToNodeX, DistanceX) in the distance vector message { d(myself, ToNodeX) = d(myself, SrcNode) + DistanceX; Determine the lowest cost between myself and ToNodeX; if ( cost/distance to ToNodeX has changed ) Schedule update message "myself, ToNodeX, d(myself, ToNodeX)" }

  • The update messages are gathered (scheduled) for a period of time and a batch of update messages are sent at the end of a period (for efficiency reasons)

• Example Distance Vector Routing

  The following is a complete run on how the distance vector routing method works... although the example may look kinda tedious, the principle is very simple (see algorithm above).

  Network topology:

  

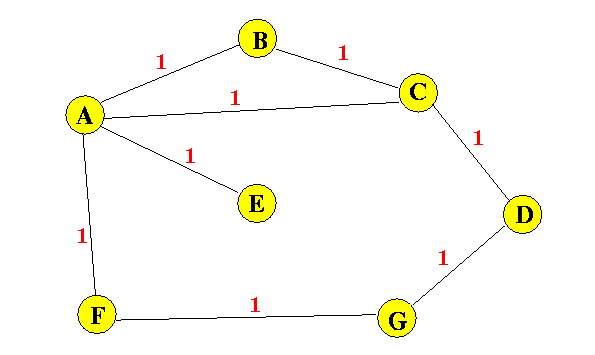
• The initial situation is as follows:

  

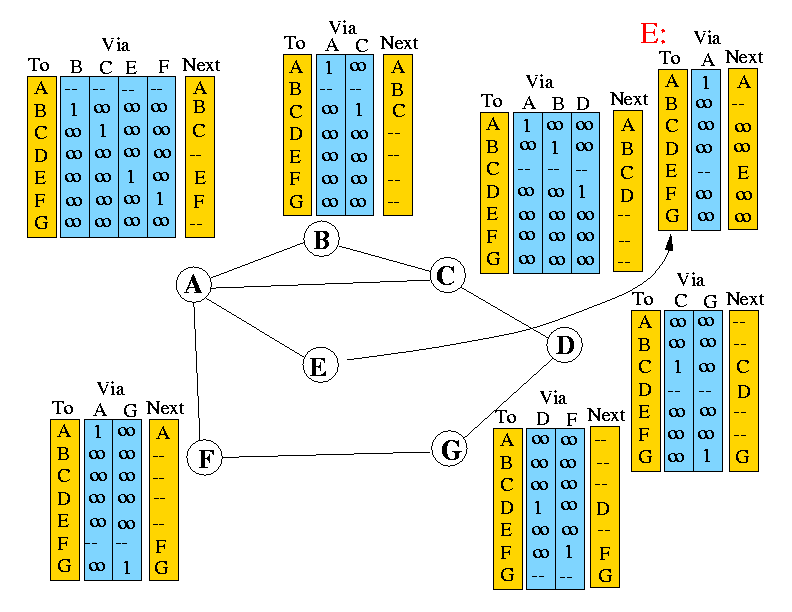
• I will make each node send an distance vector update message in turn and recompute the tables ...

  ---

• Suppose node A sends update first:

  ---

  

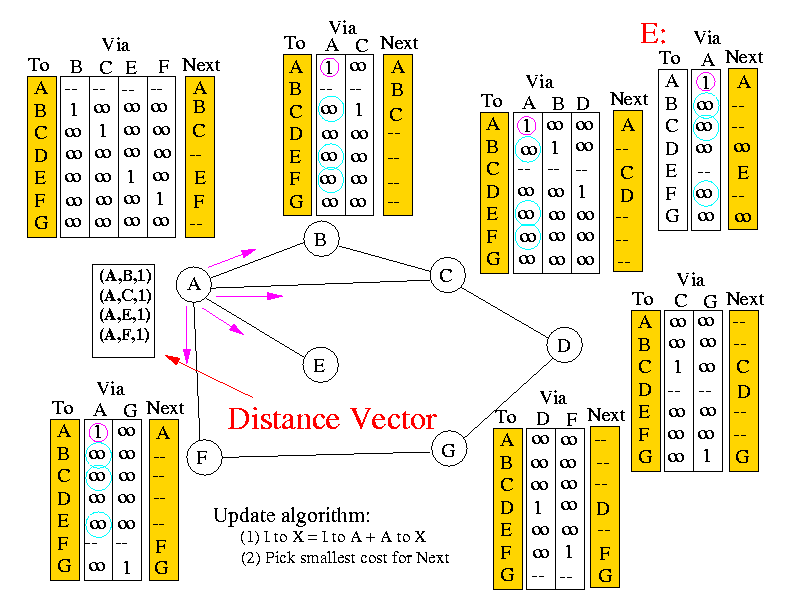
  Which will cause the following updates in tables of nodes B, C, E and F:

  

  ---

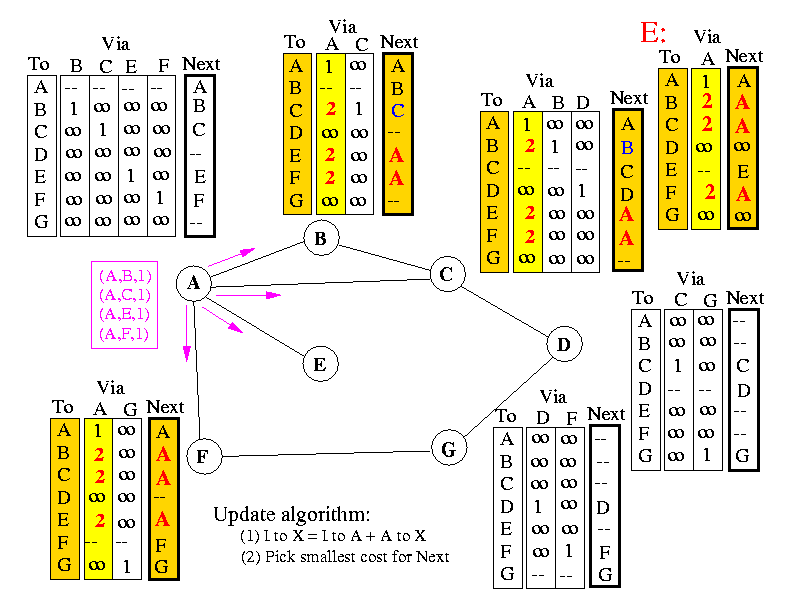
• Suppose node B transmits updates next:

  ---

  

  Which will cause the following updates in tables of nodes A and C:

  

  • Question: how can A get to F with cost 3 ???

  ---

• Suppose node C transmits updates next:

  ---

  

  Which will cause the following updates in tables of nodes A, B and D:

  

  ---

• Suppose node D transmits updates next:

  ---

  

  Which will cause the following updates in tables of nodes C and G:

  

  ---

• Suppose node G transmits updates next:

  ---

  

  Which will cause the following updates in tables of nodes D and F:

  

  • Note: here you see that the routing table entry in node D and F are updated (most of the time, a change in distance does not result in a change of route; but when the node finds a shorter route, the routing table will be updated)

  • With the gradual changes made in the routing table, you can clearly see that the Distance Vector algoritm will converge slowly to a final solution (which is the same one obtained by the Dijkstra's algorithm...)

  ---

• Suppose node F transmits updates next:

  ---

  

  Which will cause the following updates in tables of nodes A and G:

  

  ---

• Suppose node E transmits updates next:

  ---

  

  Which will cause the following updates in tables of node A:

  

  ---

• Suppose node A transmits updates next:

  ---

  

  Which will cause the following updates in tables of node B, C, E and F:

  

  ---

• Suppose node B transmits updates next:

  ---

  This will cause the following updates in tables of node B, C, E and F:

  

  ---

• Suppose node C transmits updates next:

  ---

  This will cause the following updates in tables of node A, B, and D:

  

  ---

• Suppose node D transmits updates next:

  ---

  This will cause the following updates in tables of node C, and G:

  

  ---

• Suppose node G transmits updates next:

  ---

  This will cause the following updates in tables of node D, and F:

  

  ---

• Suppose node F transmits updates next:

  ---

  This will cause the following updates in tables of node A, and G:

  

  ---

• Suppose node E transmits updates next:

  ---

  This will cause the following updates in tables of node A:

  

• Converged.....