- Previously:
- the optimal value
for hr
that minimizes the error
in a bucket br
was solved
using calculus:
- hr = Average(fsr , fsr+1 , fsr+2 , .... , fer)
The minimum error in a bucket br is:
-
Sr =
(fsr2
+ fsr+12
+ .... + fer2)
-
(fsr +
fsr+1 + ... +
fer)2/p
p = # values
- the optimal value
for hr
that minimizes the error
in a bucket br
was solved
using calculus:
- The next problem that we
must solve to find the
V-optimal histogram is
finding the best boundaries
for
the buckets
This step requires computer science...
- Jagadish et. al.
presented
a
dynamic programming approach
to find the
optimal bucket partitioning
Their paper: click here
- Problem formulation:
- Find the bucket assignment for a histogram that uses B buckets and minimizes the squared error
This problem is solved by a brute force search
(A smart brute force search :-))
- Basic idea for the search algorithm:

Meaning of the figure:
- The red area represents a
optimal histogram with k buckets
- The green area represents a
optimal histogram with k-1 buckets
- The last bucket contains the data for x, x+1, ..., b
- The red area represents a
optimal histogram with k buckets
- Suppose we need to construct a
histogram using
k-1 buckets
for the data for
a, a+1, ..., x-1
- The solution optimal histogram will be the one in the green area
Therefore:
Optimal Histogram for [a,b] using k buckets
= Optimal Histogram of [a..x-1] using k-1 buckets
+ Optimal Histogram of [x..b] using 1 buckets
- Question:
- How to determine x ???
Answer:
- There is no mathematical formula
that will tell us what is
the "best" last bucket (x..b).
- The only way
is to try every single possible case:
- Last bucket is: xN
- Last bucket is: xN-1...xN
- Last bucket is: xN-2...xN
- ...
- Last bucket is: x1...xN
One of them must have the smallest squared error
That is the optimal partition !!!
- In other words, we have the following recursive relationship:
Optimal Histogram for [a,b] using k buckets
= minx=a..b{ Optimal Histogram of [a..x-1] using k-1 buckets + last bucket is [x..b]}
- The procedure given above indicates that:
- In order to find the best histogram for [a..b] using k buckets, we must know the best histogram for every possible subrange [a..x] (x = a..b) using k-1 buckets.
- This type of algorithm is known as dynamic programming -
it is taught in CS171 (I know because I taught CS171 in Fall 2005)
Example: Computes a 2 bucket histogram with the following inputs: 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 19After processing 1 item (1):
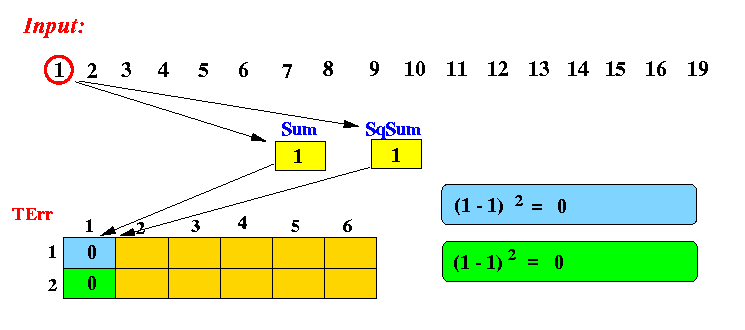
After processing 2 items (2):
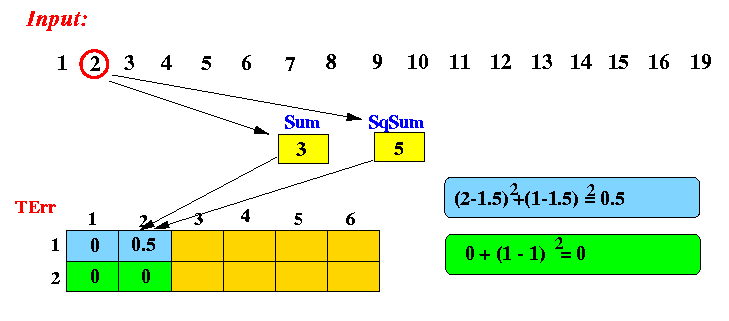
After processing 3 item (3):
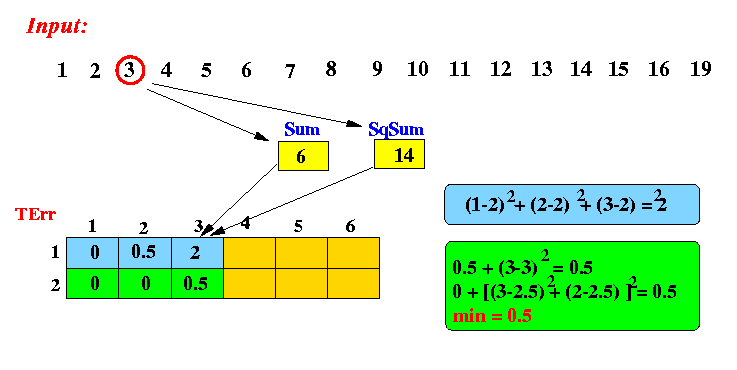
After processing 4 item (4):
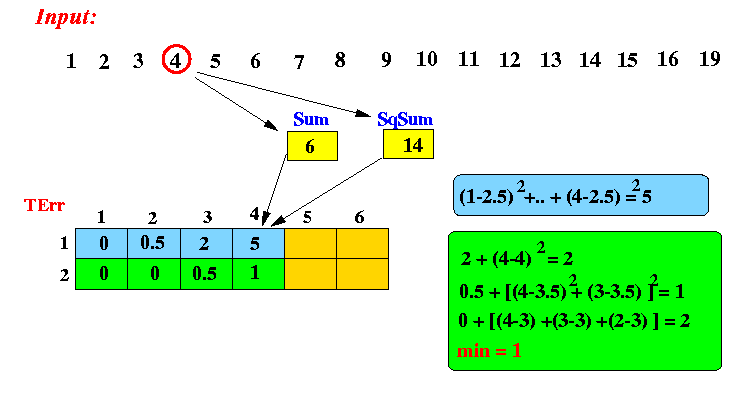
- Here is the algorithm by Jagadish:
Procedure V-Opt BestError[i][k] = best error of histogram using k buckets on (1..i) // Squared Error Function: SqError(int a, int b) { s2 = SqSum[b] - SqSum[a]; s1 = Sum[b] - Sum[a]; return (s2 - s1*s1/(b-a+1)); } // Prepare arrays to compute error efficiently Sum[0] = 0; SqSum[0] = 0; for (i = 1; i <= N; i++) { Sum[i] = Sum[i-1] + xi SqSum[i] = SqSum[i-1] + xi2 } // The dynamic algorithm to find the best histogram // // k = # buckets // i = current item - items processed are: (1..i) // BestError[i][k] = min. error in histogram of k buckets for f1..fi for (k = 1; k <= B; k++) { // Find optimal histograms for [1..k] for (i = 1; i <= N; i++) { if ( k == 1 ) BestErr[i][k] = SqError(1,i); // Single bucket (easy) else { // Multiple buckets BestError[i][k] = INFINITE; // Start value // Try every possible last bucket for (j = 1; j <= i-1; j++) // Last bucket is [j..i] { if ( BestError[j][k-1] + SqError(j+1,i) < BestError[i][k] ) { BestError[i][k] = BestError[j][k-1] + SqError(j+1,i); } } } } } - Example Program:
(Demo above code)

- Jagadish's algorithm Prog file: click here
- A version of Jagadish's algorithm that only prints the min. errors:
click here
- Sample input data file 1: click here
- Sample input data file 2: click here