- Example binary search tree:
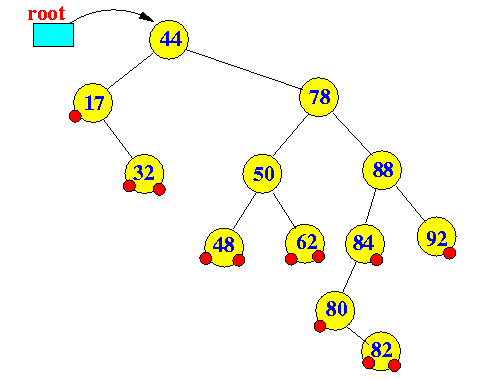
- Deleting a leaf node (no children nodes):
easy, just delete away....
Example:
- Delete 62:

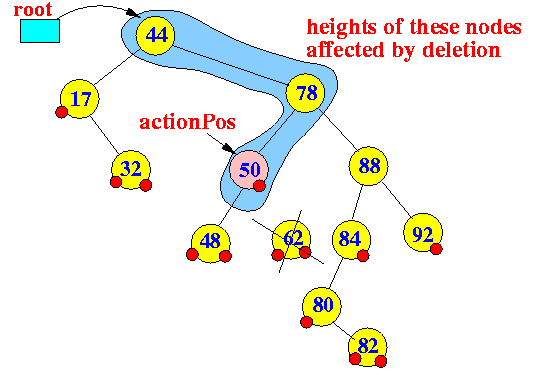
Note: action position
- The action position is
a reference to
the parent node
from which a node has been
physically removed
- The action position
indicate the first node
whose height has been
affected (possibly changed) by
the deletion
(This will be important in the re-balancing phase to adjust the tree back to an AVL tree)
- Delete 62:
- Deleting a node with 1 child node:
easy, connect its parent and child....
Example:
- Delete 84:

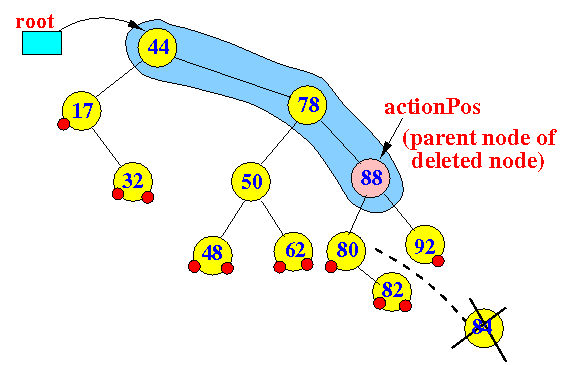
- Delete 84:
- Deleting a node with
2 children nodes:
- Replace the (to-delete) node with its in-order predecessor or in-order successor
- Then delete the in-order predecessor or in-order successor
where:
- A node's in-order successor
of a node with 2 children
is the left-most child
of its right subtree
- A node's in-order predecessor of a node with 2 children is the right-most child of its left subtree
Example: deleting using the to-delete node with its in-order successor
- Delete 78:

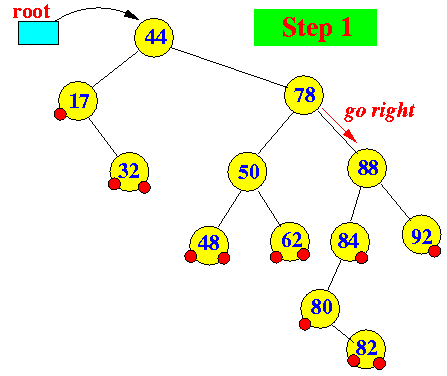
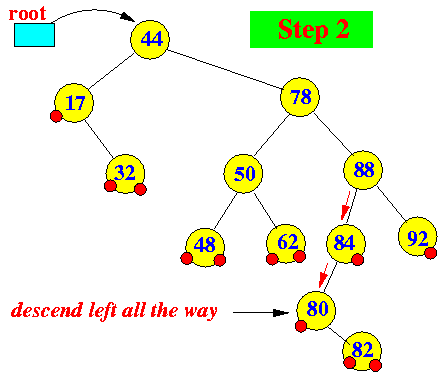
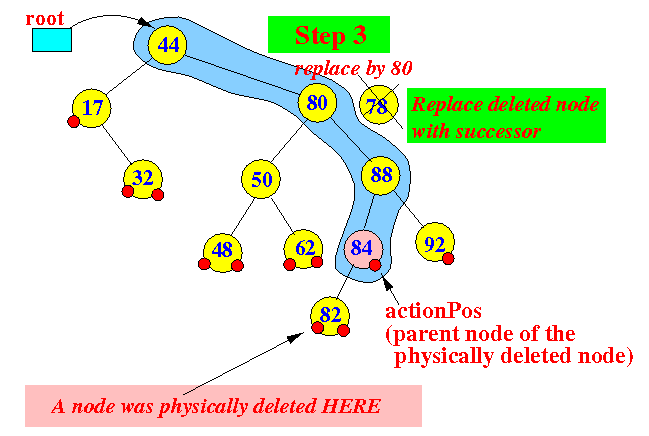
Note:
- To find out more on how to find the successor node (or the predecessor node), see: click here
- Sample AVL tree:
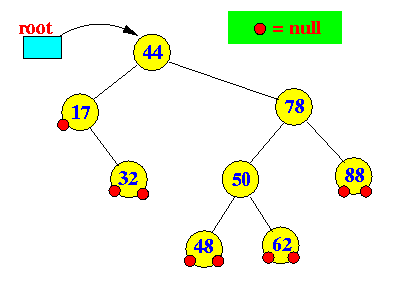
- Deleting an
entry (node) can also
cause an AVL tree to
become height unbalanced:
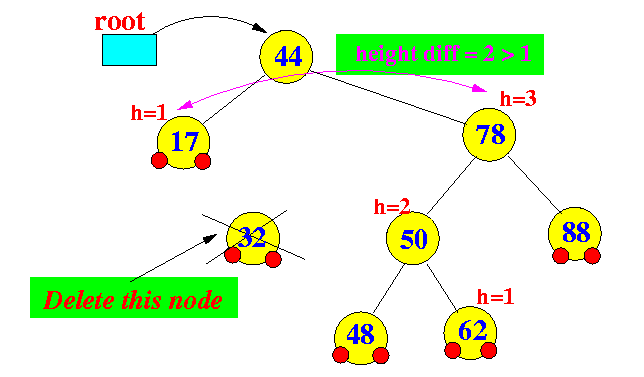
(The resulting tree is no longer an AVL tree !!)
- Recall that:
- The height changes at only nodes between the root and the parent node of the physically deleted node
- Example:
Before deleting node 32 After deleting node 32 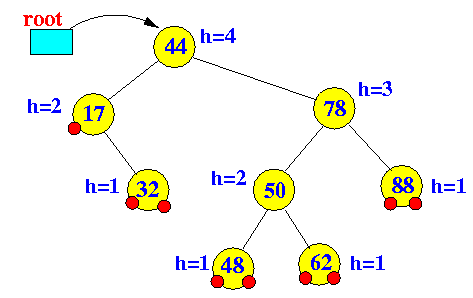
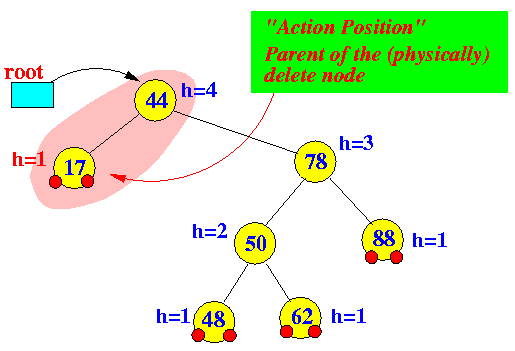
Notes:
- The actionPos (action position)
in a delete operation is the
parent node of the
"deleted" node
(By "deleted", I mean the node that is actually unlinked - not the node that was substituted by a successor node if there was a substitution === see the deleting a full internal node case above - click here)
- Just like insert,
the height of the nodes
between the
"Action Position" and
the root node
may change.
The change in this case is: decrease by 1
- The actionPos (action position)
in a delete operation is the
parent node of the
"deleted" node
- Re-balancing the AVL tree
after a delete operation:
- Just like insert operation, we can use the tri-node restructure operations to re-balance an out-of-balanced AVL tree.
Important difference:
- How to apply the tri-node restructure operations is a bit tricky in the delete operation.
- Example:
re-balancing
an AVL tree after a
deletion:
- Starting at the
action position
(= parent node of the
physically deleted node),
find the
first imbalanced node
(This step is exactly the same as in insert)
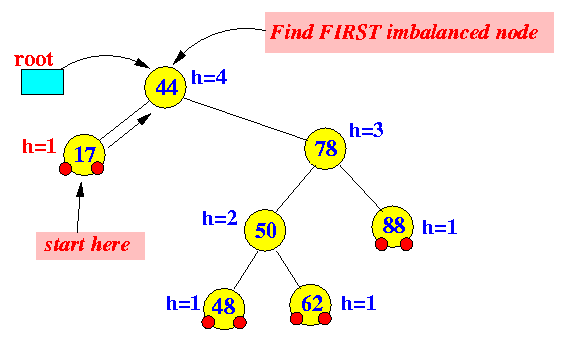
- Perform a
tri-node restructure operation
using these 3 nodes (shaded):
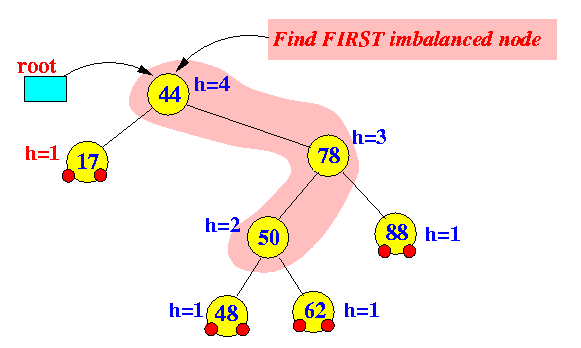
- For clarity sake,
I have depicted the
movement of
the 3 nodes in this figure first:
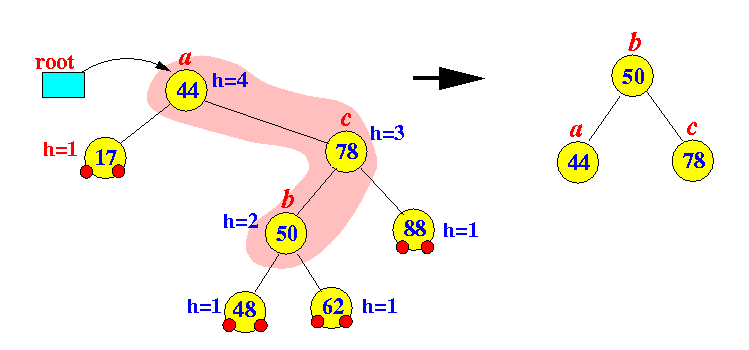
- The tree after the
tri-node restructure operation is:
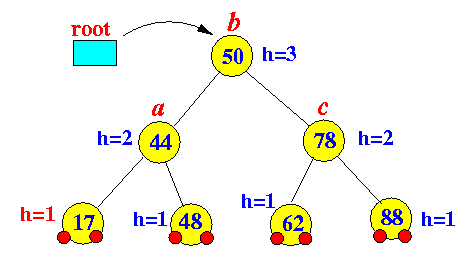
You can see it is an AVL tree....
- Starting at the
action position
(= parent node of the
physically deleted node),
find the
first imbalanced node
- Let us look at the state of
the imbalanced AVL tree
prior to applying the
tri-node restructure operation
in the insert operation:
- AVL tree
before
inserting a new node:
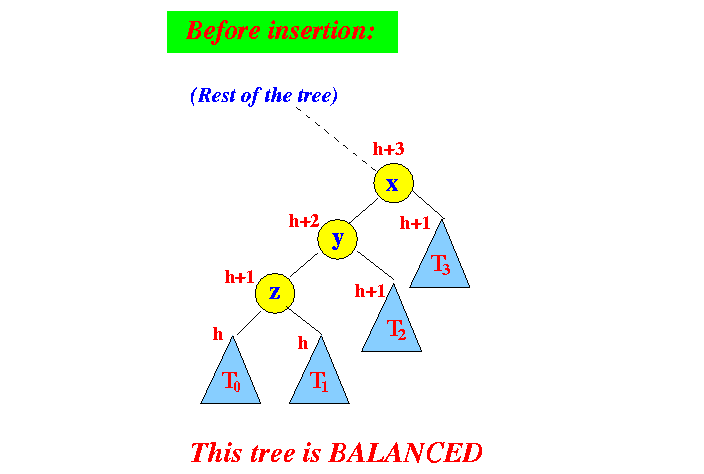
- AVL tree
after
inserting a new node:
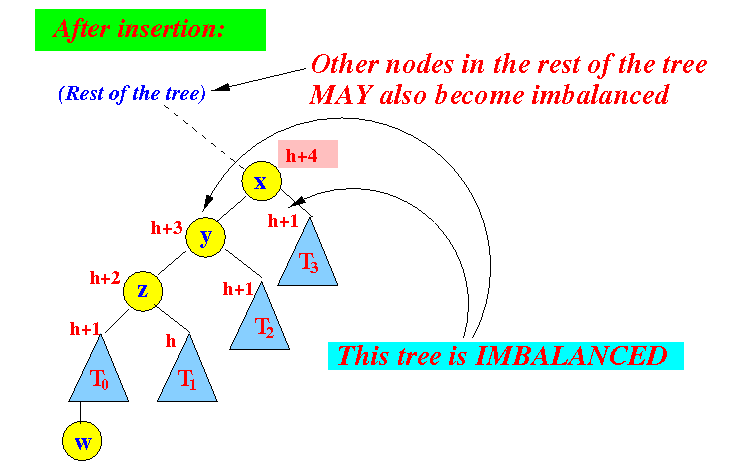
- Notice that:
- AVL tree
before
inserting a new node:
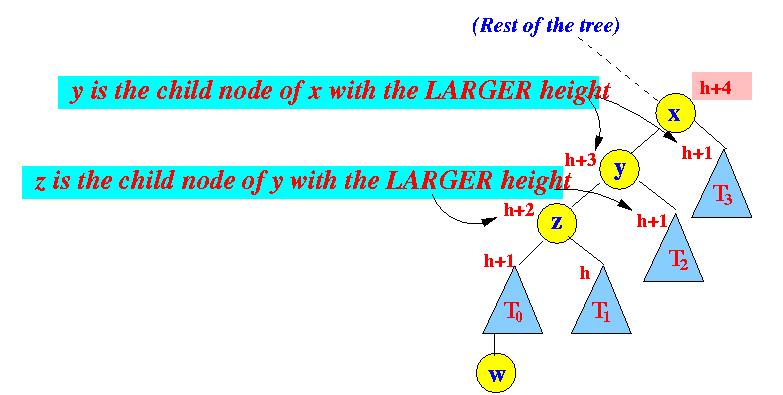
- Pre-conditions for
apply a
tri-node restructure operation
to re-balance an AVL tree:
- Node x = the
first imbalanced node
from the action position
(= parent of the
physically
inserted/deleted node) to the
root.
- Node y =
the child node of
node x
that has the
higher height
- Node z = the child node of node y that has the higher height
- Node x = the
first imbalanced node
from the action position
(= parent of the
physically
inserted/deleted node) to the
root.
- A preliminary version
(incomplete !!)
of the
re-balance algorithm
for the delete operation:
Starting at the action position node (= parent node of the physically delete node): { find the first node p that is imbalanced } /* ----------------------------------------------- Identify grandchild node of the unbalanced node for the restructure operation ----------------------------------------------- */ x = p; y = the taller Child of x; z = the taller Child of y; tri-node-restructure( x, y, z ); // Apply the tri-node reconf. op.
Example:
- Delete node 32:

- Start the search
at the action position node (17)
(= parent node of the
physically deleted node (32)):

- traverse up the tree
towards the root node
to find the
first node p
that is unbalanced
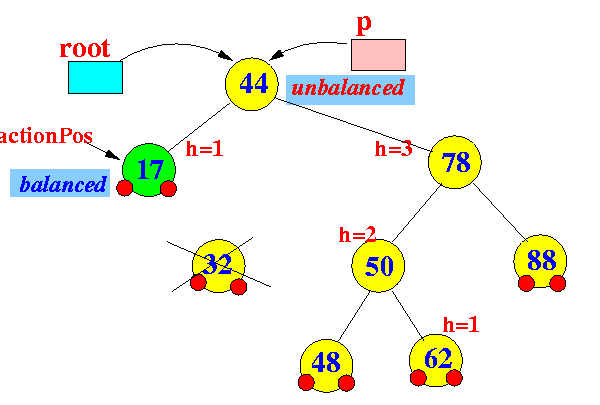
Found: node 44
- Determine
x,
y and
z for
the tri-node restructure operation:
x = p; ====> x = 44 y = taller child of x; ====> y = 78 z = taller child of y; ====> z = 50Graphically:
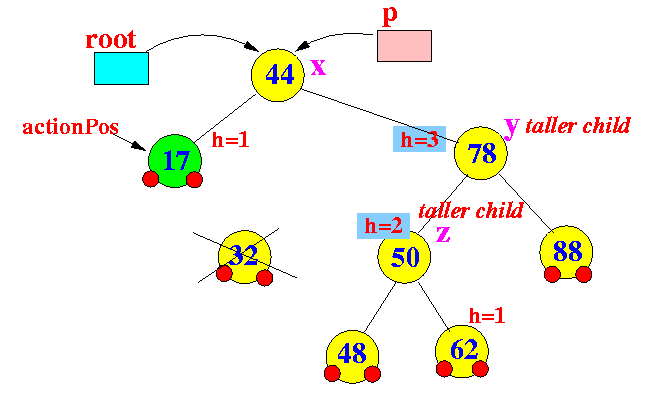
- Now apply
tri-node-restructure(x,y,z):
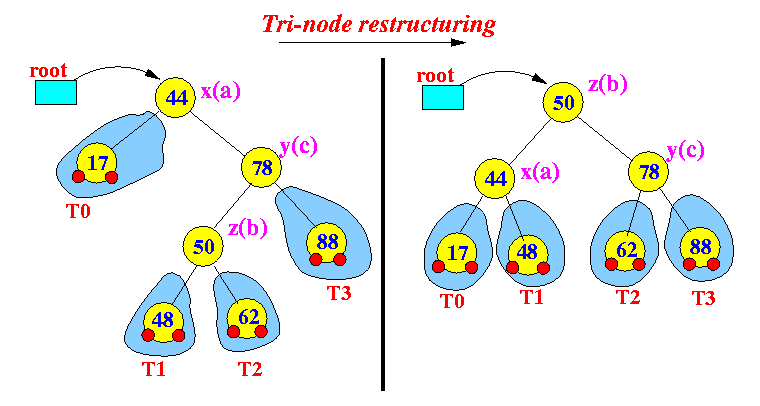
- Delete node 32:
- Facts:
- We just saw that:
- The imbalance at the first imbalance node due to a deletion operation can be restored using a tri-node restructure operation
- However:
- The resulting subtree does not have the same height as the original subtree !!!
- Consequently:
- Node that are further up the tree are not re-balanced by the re-balancing of the first imbalanced node !!!
- We just saw that:
- Example:
- Consider the following AVL tree:
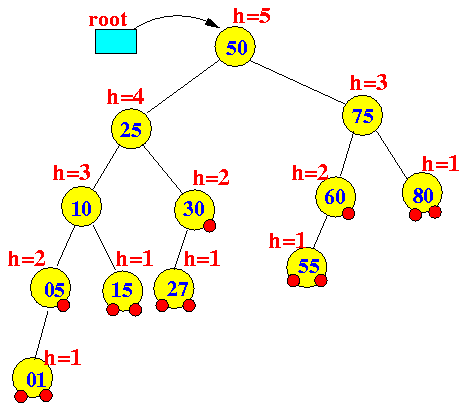
Notice that the original height of this (shaded) subtree is 3:
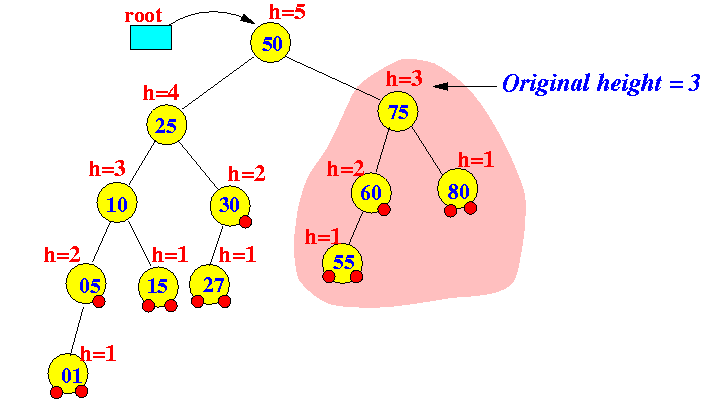
- Delete the node 80:
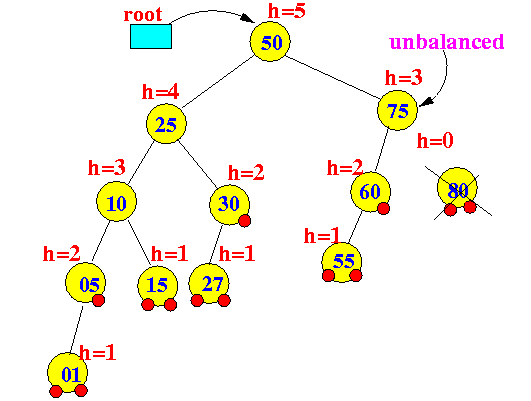
- Perform a Tri-node restructuring:
Tree before restructuring Tree after restructuring 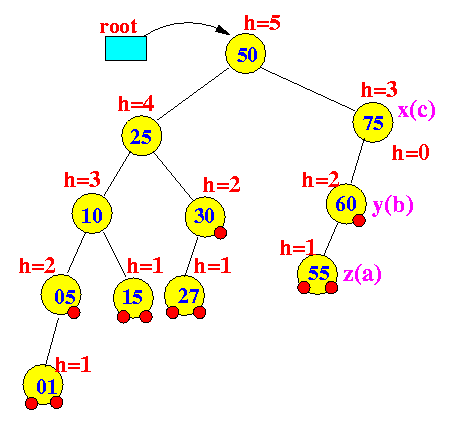
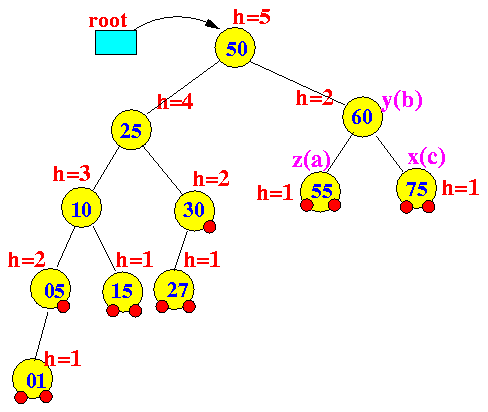
- Notice that the
resulting subtree
is shorter
than the original subtree !!!
Original subtree 
Resulting subtree 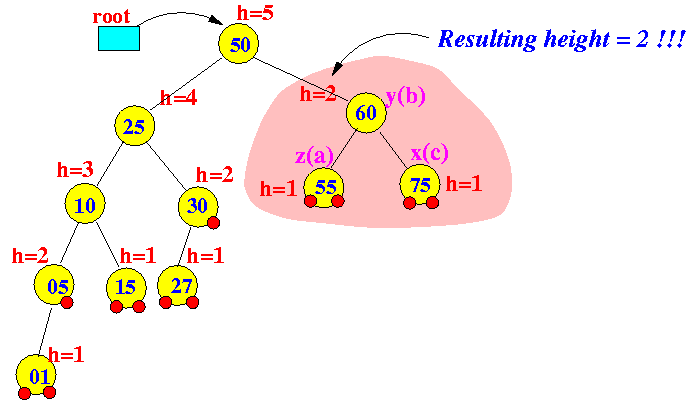
Result:
- Nodes
further up in the tree
can
become
imbalanced !!!
Example:
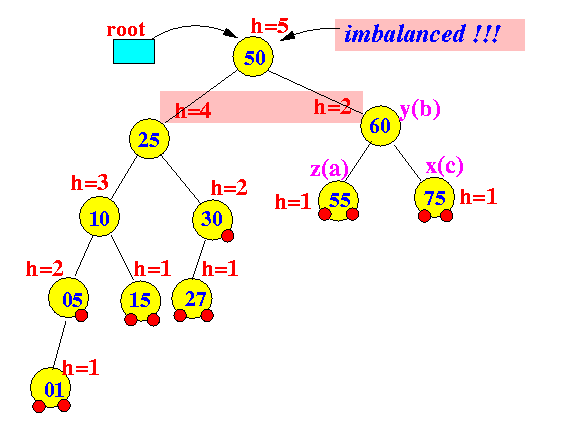
- Consider the following AVL tree:
- Comment:
- This problem
(see above)
does not occur
in the insert operation
because the
height of
the resulting subtree
was equal to
the original tree
- We has this situation in
an insert operation:
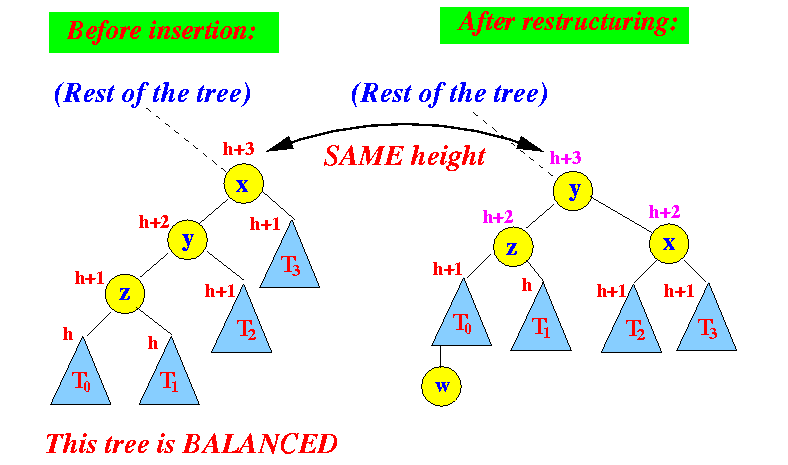
- So we don't have to perform the tri-node restructure operation on node further up the tree in an insert operation !
- This problem
(see above)
does not occur
in the insert operation
because the
height of
the resulting subtree
was equal to
the original tree
- Re-balancing algorithm for the deletion:
p = action position; // Starting point while ( p != root ) // Travel all the way up the tree !!! { if ( p is unbalanced ) { /* ----------------------------------------------- This the is first imbalanced node (i.e., x) ----------------------------------------------- */ x = p; /* --------------------------------------------------- Identify nodes y and z for the restructure operation --------------------------------------------------- */ y = the taller Child of x; z = the taller Child of y; p = tri-node-restructure(x, y, z); // NOTE: we MODIFY tri-node-restructure() to // return the root node of the NEW subtree !!! } p = p.parent; // traverse twards the root }
- Java implementation:
public void rebalance(BSTEntry p) // The starting point is passed as parameter !!! { BSTEntry x, y, z, q; while ( p != null ) { if ( diffHeight(p.left, p.right) > 1 ) { x = p; y = tallerChild( x ); z = tallerChild( y ); System.out.println("tri_node_restructure: " + x + y + z); p = tri_node_restructure( x, y, z ); } p = p.parent; } }
- The (slightly) modified
tri-node restructure method:
public BSTEntry tri_node_restructure( BSTEntry x, BSTEntry y, BSTEntry z) { .... Same old code ..... (See: click here) return b; // We return the root of the new subtree }
- remove() in Java:
I have high lighted
the re-balance() calls
/* ====================================================== This is the SAME remove method as BST tree, but with rebalance() calls inserted after a deletion to rebalance the BST.... ====================================================== */ public void remove(String k) { BSTEntry p, q; // Help variables BSTEntry parent; // parent node BSTEntry succ; // successor node /* -------------------------------------------- Find the node with key == "key" in the BST -------------------------------------------- */ p = findEntry(k); if ( ! k.equals( p.key ) ) return; // Not found ==> nothing to delete.... /* ======================================================== Hibbard's Algorithm ======================================================== */ if ( p.left == null && p.right == null ) // Case 0: p has no children { parent = p.parent; /* -------------------------------- Delete p from p's parent -------------------------------- */ if ( parent.left == p ) parent.left = null; else parent.right = null; /* -------------------------------------------- Recompute the height of all parent nodes... -------------------------------------------- */ recompHeight( parent ); /* -------------------------------------------- Re-balance AVL tree starting at ActionPos -------------------------------------------- */ rebalance ( parent ); // Rebalance AVL tree after delete at parent return; } if ( p.left == null ) // Case 1a: p has 1 (right) child { parent = p.parent; /* ---------------------------------------------- Link p's right child as p's parent child ---------------------------------------------- */ if ( parent.left == p ) parent.left = p.right; else parent.right = p.right; /* -------------------------------------------- Recompute the height of all parent nodes... -------------------------------------------- */ recompHeight( parent ); /* -------------------------------------------- Re-balance AVL tree starting at ActionPos -------------------------------------------- */ rebalance ( parent ); // Rebalance AVL tree after delete at parent return; } if ( p.right== null ) // Case 1b: p has 1 (left) child { parent = p.parent; /* ---------------------------------------------- Link p's left child as p's parent child ---------------------------------------------- */ if ( parent.left == p ) parent.left = p.left; else parent.right = p.left; /* -------------------------------------------- Recompute the height of all parent nodes... -------------------------------------------- */ recompHeight( parent ); /* -------------------------------------------- Re-balance AVL tree starting at ActionPos -------------------------------------------- */ rebalance ( parent ); // Rebalance AVL tree after delete at parent return; } /* ================================================================ Tough case: node has 2 children - find successor of p succ(p) is as as follows: 1 step right, all the way left Note: succ(p) has NOT left child ! ================================================================ */ succ = p.right; // p has 2 children.... while ( succ.left != null ) succ = succ.left; p.key = succ.key; // Replace p with successor p.value = succ.value; /* -------------------------------- Delete succ from succ's parent -------------------------------- */ parent = succ.parent; // Prepare for deletion parent.left = succ.right; // Link right tree to parent's left /* -------------------------------------------- Recompute the height of all parent nodes... -------------------------------------------- */ recompHeight( parent ); /* -------------------------------------------- Re-balance AVL tree starting at ActionPos -------------------------------------------- */ rebalance ( parent ); // Rebalance AVL tree after delete at parent return; }
- Example Program:
(Demo the insert operation in AVL tree)

- The AVL Tree class file: click here
- The BSTEntry.java class file:
click here
- Remove Test program 1 (No propagation of the re-structuring operation): click here
- Remove Test program 2: (with propagation of the re-structuring operation): click here
- Output of Remove Test Prog2:
(I made some annotations to the output...)