- Classic TCP:
1 Increase: W = W + --- (when new ACK is received) W Decrease: W = W - 0.5 * W (when packet loss is detected by 3 dup ACKs)
1 1.2 Avg TCP Throughput = ----- * ------- (in # packets/sec) RTT --- \/ p p = packet loss probability
- The average CWND
used by (classic) TCP:
- Throughput when using
CWND = k (packets):

What value of CWND used by TCP will yield the average TCP throughput:
1 1.2 Avg TCP Throughput = ----- * ------- (in # packets/sec) RTT --- \/ p
- Throughput when using
CWND = k (packets):
- Relationship:
1.2 Avg. CWND = ------- (in # packets) --- \/ p
- Some explicit values:
- Floyd in RCF 3649, has established experimentally that an
average congestion window of
W
corresponds to an average of
2/3 W
round-trip times between loss events for Standard TCP
- The 3rd column shows the average time between losses.
- NOTE:
-
We can see in this table, that under a
very low packet frop probability
of p = 10-7,
the standard TCP protocol will
ONLY use a CNWD of 3795
This CWND value will NOT allow TCP to transmit at Giga bits per sec
(= 2/3 * W) Packet Drop Rate P Congestion Window W RTTs Between Losses ------------------ ------------------- ------------------- 10^-2 12 8 10^-3 38 25 10^-4 120 80 10^-5 379 252 10^-6 1200 800 10^-7 3795 2530 10^-8 12000 8000 10^-9 37948 25298 10^-10 120000 80000 Table 2: TCP Response Function for Standard TCP. The average congestion window W in MSS-sized segments is given as a function of the packet drop rate P.
- Floyd in RCF 3649, has established experimentally that an
average congestion window of
W
corresponds to an average of
2/3 W
round-trip times between loss events for Standard TCP
- The
Average Generalized TCP Throughput
is given by the formula
(See: click here):
a Increase: W = W + --- W Decrease: W = W - b * W ------------ 1 / a (2 - b) Avg TCP Throughput = ----- \ / ---------- (# packets/sec) RTT \/ 2bp - We can also conclude that the
Average TCP CWND
is:
------------ / a (2 - b) Avg TCP CWND = \ / ---------- (# packets) \/ 2bp
- Notice that there are
4 unknowns
in this relationship:
- a
- b
- p
- CWND
(RTT is not an unknown, it can be measured by the TCP connection)
That means that we can choose the value of 3 unknowns (i.e., parameters) and the value of the 4th unknown is fixed
- Clearly, the
packet loss probability p
is a
parameter
(you cannot "choose" a loss probability)
- As we will see later, the
congestion window CWND
will also be
chosen.
- Choosing
a value of a paramater is akin to
making a certain assumption
or
trying to achieve a certain goal
- For example:
-
When we choose to set
the packet loss probability p
to a value of - say -
0.00000001 ,
then we are making a certain assumption
about the packet loss probability.
-
When we choose to set
the congestion window CWND
to a value of - say -
10000 ,
then we are trying to achieve a certain goal
for the congestion window
- The key is to obtaining a High Speed
TCP protocol is to use:
-
A bigger (general) increase
to bridge the large amount of bandwidth that
TCP need to obtain in a
High Speed
network
- However,
we must remember that the "ordinary (Reno) TCP" will
NOT go away
when we introduce a "high speed TCP".
In other words:
-
High speed TCP must
co-exist
with "normal" (Reno) TCP
- Herein lies the
difficulty
in the design
(if we can tossed out "Ordinary Reno", any speedier increase
and decrease will work):
-
A High speed version of TCP must
be "friendly"
to the "normal" (Reno) TCP
In other words, when a High speed version of TCP and a "normal" (Reno) TCP compete for bandwidth over a common bottle neck link, the "normal" (Reno) TCP must be starve for bandwidth
We call this property: "TCP-friendly"
- Fact 1:
-
When the packet loss probability is high,
TCP's congestion window CWND
will be
relatively small
and transmission speed can never reach
Giga bits per sec
- Fact 2:
-
When a High Speed version of TCP encounters
congestion
(e.g., transmits over a slower link), it will encounter
a high packet loss probability,
and consequently,
its congestion window CWND
will be
relatively small
- Armed with these 2 fact, we can summarizes
the "High Speed TCP" algorithm:
- The HighSpeed TCP
will use a
dynamic
(not static) increase and decrease functions
that
depended on its current CWND
value.
- To be TCP-friendly ,
the increase and decrease functions used when
CWND is small ( < Low_Window)
is the same one used by Reno
- When CWND is large( > Low_Window) (i.e., no congestion), faster increase/decrease functions are used.
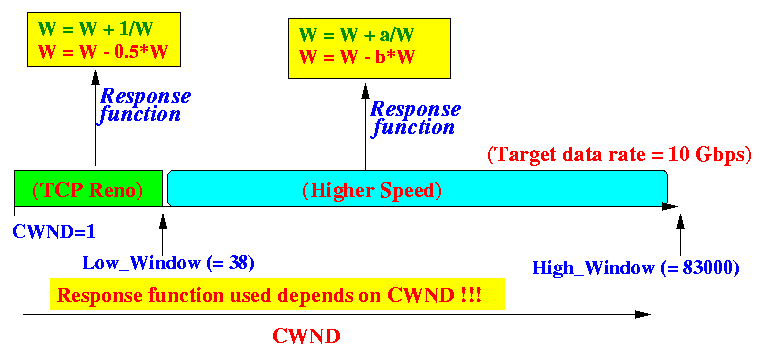
- The HighSpeed TCP
will use a
dynamic
(not static) increase and decrease functions
that
depended on its current CWND
value.
- Here is the description of the design of HighSpeed TCP
in the authors' own words:
-
To specify the
upper end of the HighSpeed response function, we
specify the packet drop rate needed in the HighSpeed response
function to achieve an average congestion window of
83000 segments.
This is roughly the window needed to sustain
10 Gbps throughput, for
a TCP connection with the default packet size
(= 1500 bytes)
and round-trip time (= 0.1 sec)
used earlier in this document.
(Avg. Throughput is then: 83,000x1500x8/0.1 = 9,960,000,000 bps or about 10 Mbps)
For High_Window set to 83000, we specify (i.e., our guess) High_P equal to 10-7; that is:
-
with HighSpeed TCP, a packet drop
rate of 10-7 will allow
the HighSpeed TCP connection to achieve an
average congestion window of 83000 segments.
We believe that this loss rate sets an achievable target for high-speed environments, while still allowing acceptable fairness for the HighSpeed response function when competing with Standard TCP in environments with packet drop rates of 10-4 or 10-5.
(See Page 6 in "RFC3649: HighSpeed TCP for Large Congestion Windows")
- The following figure clarifies the design idea of
HighSpeed TCP:
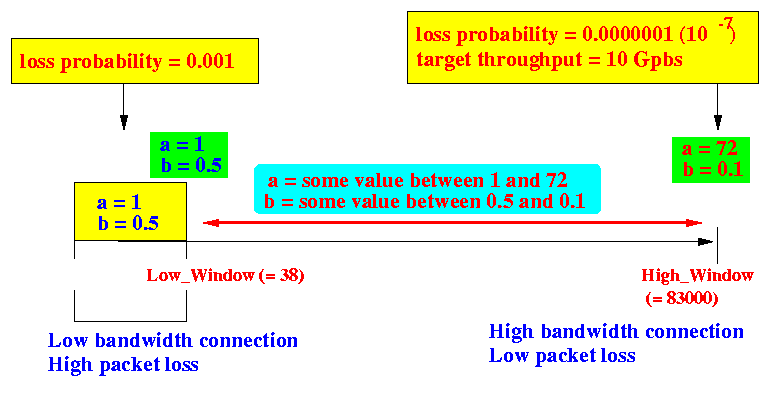
- First, they made sure that
the HighSpeed TCP will be
compatible
with Ordinary TCP in
low speed
(=> high loss probability => small CWND)
range
- Then they make up
a
best case scenario target which is
obtained using 2 assumptions:
- Packet loss probability
is very small, estimated at:
10-7
- Targeted TCP throughput is 10 Gbps using a packet size of 1500 bytes and a RTT of 0.1 sec
This works out (see above) to a target CWND = 83000
For this best case scenario , they found values of TCP increase/descrease parameters a (e.g.: 72) and b (e.g.: 0.1) that will allow TCP's CWND to work its way towards the target CWND of 83000
- Packet loss probability
is very small, estimated at:
10-7
- For a situation that lies in between the
low bandwidth (small CWND)
and
highest bandwidth (CWND = 83000),
they
interpolate
the TCP increase/decrease parameter
a
and
b
- The low end (CWND < 38) uses
a = 1
and
b = 0.5
- The high end (CWND < 83000) uses
a = 72
and
b = 0.1
- When 38 < CWND < 83000 ,
the TCP increase/decrease parameters:
- a is a value between 1 and 72
- b is a value between 0.1 and 0.5
- The low end (CWND < 38) uses
a = 1
and
b = 0.5
- First, they made sure that
the HighSpeed TCP will be
compatible
with Ordinary TCP in
low speed
(=> high loss probability => small CWND)
range
- Just to give you an idea how we can determine
the TCP's increase/descrease parameter
a
and
b ,
let us do an example.
-
How did they get the values:
a = 72
and
b = 0.1
to allow TCP to achieve CWND = 83,000 ???
- Recall that these setting were used for
Recall that these setting were used for
the High End of their target rate:
Target packet drop probability = 10-7 Target CWND = 83000
- To find a TCP increase/descrease parameter
a
and
b that
allows TCP to achieve
CWND = 83,000 when the
packet drop probability = 10-7,
we use the formula:
------------ / a (2 - b) Avg TCP CWND = \ / ---------- \/ 2bp
- After substituting CWND = 83,000 when the
p = 10-7, we still have
2 degrees of freedom
(i.e., 2 unknowns):
------------------ / a (2 - b) 83000 = \ / ---------- * 107 \/ 2b
- There are many solutions possible
and you can verify that
a = 72
and
b = 0.1
is one of the solutiuons:
--------------------- / 72 (2 - 0.1) \ / ------------- * 107 \/ 2*0.1 ------------------ / 72 * 1.9 = \ / ---------- * 107 \/ 0.2 -------- / = \ / 684 * 107 \/ = 82704.29 (approximately 83000)
- Another solution
is
a = 459
and
b = 0.5:
--------------------- / 459 (2 - 0.5) \ / ------------- * 107 \/ 2*0.5 ------------------ / 459 * 1.5 = \ / ---------- * 107 \/ 1.0 -------- / = \ / 688.5 * 107 \/ = 82975.90 (also approximately 83000)
- Which solution is better ?
- If the chase of
a = 459
and
b = 0.5,
the HighSpeed TCP connection will
add 459 packets
in each round of transmission (ball-park approximate 0.1 sec).
That's 4590 packets in a second...
This could cause severe buffer overflow
- If the chase of
a = 72
and
b = 0.1,
the HighSpeed TCP connection will
add 72packets
in each round of transmission (ball-park approximate 0.1 sec).
That's 720 packets in a second...
This is obviously a much gentler solution
- BTW, the parameters
a
and
b are dependent
on each other,
when you use a larger
a
you will also need to use a larger
b
- If the chase of
a = 459
and
b = 0.5,
the HighSpeed TCP connection will
add 459 packets
in each round of transmission (ball-park approximate 0.1 sec).
- Bottomline:
-
The designers of HighSpeed TCP has chosen a low
(a, b)
pair to achieve CWND = 83,000 in the
most favorable condition.
The choice they have made is: a = 72 and b = 0.1
- Here is the situation graphically:
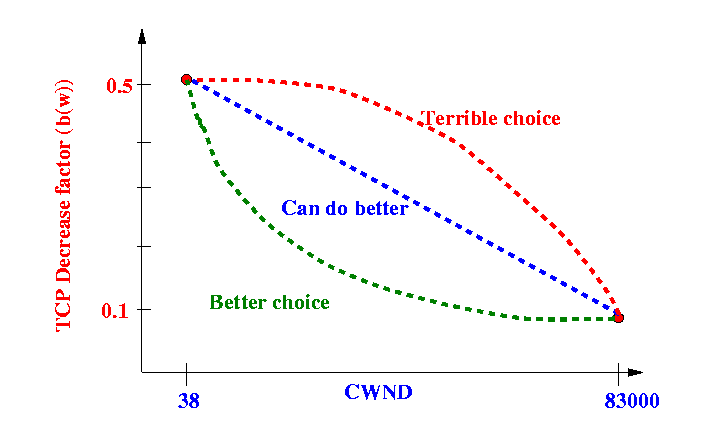
- We have
2 operational points
- Find the "best" interpolation function

- We have
2 operational points
- There are many
interpolation functions
possible:
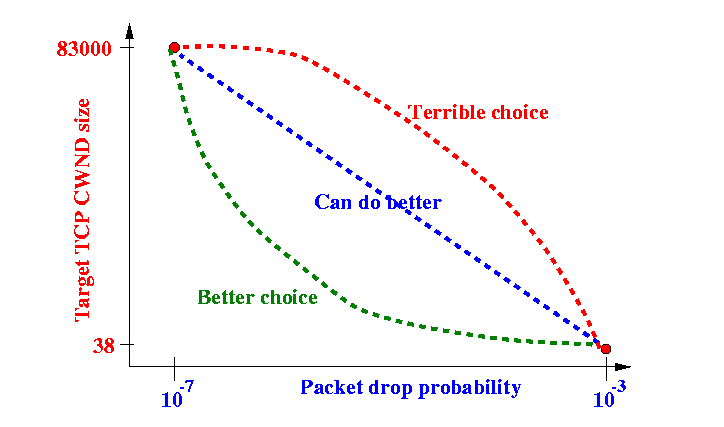
- The Red curve will start using
HIGH increases in CWND
when
packet drop probability is still
very high, not a good thing.
- The Blue interpolation line is OK, but we can do better
- The Green curve will use LOW increases in CWND when packet drop probability is still high and will only start HIGH increase in CWND when the packet drop probability is very low - obviously, this is the better interpolation method.
- The Red curve will start using
HIGH increases in CWND
when
packet drop probability is still
very high, not a good thing.
- The authors propose to use the following
interpolation function:
on CWND and p
0.12 W(p) = --------- . . . . . . . . . . . . . . (1) 0.835 p
W(10-3) = 38.3867 (= 38) W(10-7) = 83981.04 (= 83000) u Basically, they wanted a curve of the form: ---- pv And they solved: u -------- = 38 (0.001)v u ------------ = 83000 (0.0000001)v - The following is a plot of the
proposed interpolation curve on a linear scale.
It is very obvious that TCP will use a very large CWND only when the packet drop probability is very low:
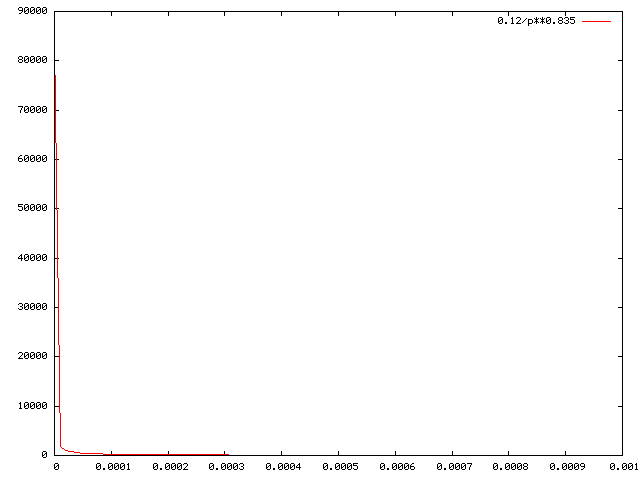
- The following is a plot of the
proposed interpolation curve on a
a log-log scale.
it is a straight line going through the design points: (p=10-7, W=83000) and (p=10-3, W=38)
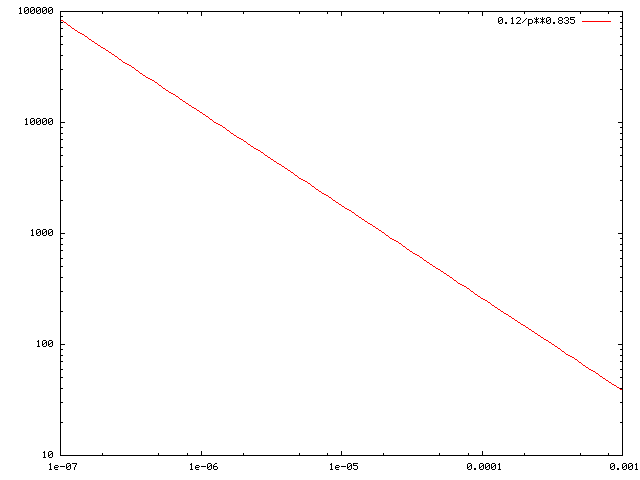
Why it is a straight line on a log-log scale is obvious when we re-write the Interpolation function as follows:
0.12 W(p) = --------- 0.835 p
log( W(p) ) = log(0.12) - log( p0.835 )
log( W(p) ) = log(0.12) - 0.835 * log( p ) // Linear...
- The following is a Tabular Respresentation of the
interpolation function:
Packet Drop Rate P Congestion Window W RTTs Between Losses ------------------ ------------------- ------------------- 10^-2 12 8 10^-3 38 25 10^-4 263 38 10^-5 1795 57 10^-6 12279 83 10^-7 83981 123 10^-8 574356 180 10^-9 3928088 264 10^-10 26864653 388 Table 3: TCP Response Function for HighSpeed TCP. The average congestion window W in MSS-sized segments is given as a function of the packet drop rate P.
- We will need the inverse relationship in the near future,
so, let us calculate that first:
0.12 W = --------- 0.835 p
0.12 p0.835 = ------ W
0.121.1976 p(W) = ------------ W1.1976
0.0789 p(W) = --------- . . . . . . . . . . . . . (2) W1.2
- Because TCP Reno uses
Additive Increase Multiplicative Decrease as
congetion control,
the HighSpeed response function
has to be
translated
into additive increase and multiplicative
decrease parameters.
- The Additive Increase Multiplicative Decrease
mechanism in HighSpeed TCP is changed into:
- Note that
w
is the
current congestion window (CWND)
TCP knows exactly what w is.
- Note also that: Standard TCP uses: a(w) = 1 and b(w) = 0.5, independent of w
a(w) Increase: w <- w + ------ w Decrease: w <- w - b(w) * w
- Note that
w
is the
current congestion window (CWND)
- We know that
a(w)
and
b(w)
must satisfy the following relationship:
------------------ / a(w) (2 - b(w)) w = \ / ---------------- (# packets) \/ 2 b(w) p
2 a(w) (2 - b(w)) w = ----------------- 2 b(w) p
a(w) * (2 - b(w)) = w2 * 2 * b(w) * p
2 w2 b(w) p a(w) = -------------- 2 - b(w)
Or better written as: 2 w2 b(w) p(w) a(w) = ---------------- . . . . . . . . . (3) 2 - b(w) because p changes as w changes.Notice that there are ONLY TWO degrees of freedom in Equation (3):
- a(w)
- b(w)
The value p(w) is not really variable because it can be found by INTERPOLATION using Equation (2): click here
0.0789 p(W) = --------- W1.2 - In other words:
-
We need to fix
(i.e., find an approximate value )
for one of the parameters
a(w) or b(w), and
we can compute the other one.
- In fact, we have
Equation (3) written so neatly that it's
a no-brainer
that we should do is:
- find an approximate value
for b(w)
and
- use Equation (3) to compute a(w) :-)
- find an approximate value
for b(w)
and
- To find an approximation for
b(w) ,
we use the
same old trick:
Interpolation
- Again, consider the following 3 possible interpolation curves -
now for
b(w) :
- A larger value
for
b(w)
makes TCP decreases more - i.e.,
more fluctuations.
- When CWND is
high,
the
fluctuations
are
stronger.
Large fluctuations generally make a system unstable
To compensate (i.e., reduce) the larger fluctuations we make b smaller quickly
- Therefore, the Green interpolation curve is better (this hass not been verified scientifically however).
- A larger value
for
b(w)
makes TCP decreases more - i.e.,
more fluctuations.
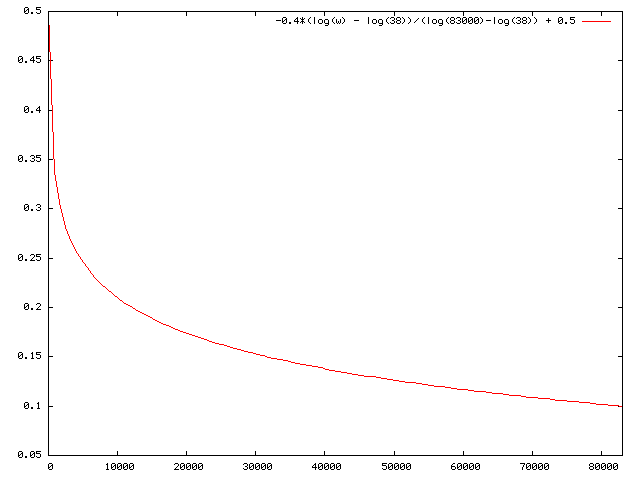
- The designers of the HighSpeed TCP protocol uses the following
Interpolation curve for
b(w) :
log(w) - log(38) b(w) = (0.1 - 0.5) * ---------------------- + 0.5 . . . . . (4) log(83000) - log(38)
The Interpolation curve for b(w) looks like this:
- In case you got lost in the details, here is a recipe
to implement the HighSpeed TCP protocol
a(w) New ACK: w <- w + ------ w Triple Dup ACK: w <- w - b(w) * w
- To perform a DECREASE when
Triple Duplicate ACKs are detected:
We compute the parameter b(w) using the current CWND value w and the formula:
log(w) - log(38) b(w) = (0.1 - 0.5) * ---------------------- + 0.5 log(83000) - log(38)So if HighSpeed TCP performs a CWND decrease, this is all the TCP needs.
- To perform a INCREASE when
a new ACK is received:
HighSpeed TCP must do a lot more:
- It must first computes
p(w)
using:
0.0789 p(W) = --------- W1.2 - Then computes
b(w)
using
log(w) - log(38) b(w) = (0.1 - 0.5) * ---------------------- + 0.5 log(83000) - log(38) - Finally compute a(w)
using
2 w2 b(w) p(w) a(w) = ---------------- 2 - b(w) - Increase using: a(w)/w
- It must first computes
p(w)
using:
- The code of the HighSPeed TCP in NS2 can be found in
NS-DIR/tcp/tcp.cc:
click here
Look for the method "double TcpAgent::increase_param()".
Here is a "cleaned up" code segment of the HighSpeed TCP algorithm:
# These are all used for high-speed TCP. Agent/TCP set low_window_ 38 ; # default changed on 2002/8/12. Agent/TCP set high_window_ 83000 Agent/TCP set high_p_ 0.0000001 # 10^-7 Agent/TCP set high_decrease_ 0.1 Agent/TCP set max_ssthresh_ 0 double TcpAgent::increase_param() { double increase, decrease, p, answer; // p ranges from 1.5/W^2 at congestion window low_window_, to // high_p_ at congestion window high_window_, on a log-log scale. // The decrease factor ranges from 0.5 to high_decrease // as the window ranges from low_window to high_window, // as the log of the window. // For an efficient implementation, this would just be looked up // in a table, with the increase and decrease being a function of the // congestion window. if (cwnd_ <= low_window_) { answer = 1 / cwnd_; // Standard Reno return answer; } else { // hstcp_.p1 = log(hstcp_.low_p) // - log(low_window_) * highLowP/highLowWin; // hstcp_.p2 = highLowP/highLowWin; // hstcp_.dec1 = 0.5 - log(low_window_) // * (high_decrease_ - 0.5)/highLowWin; // hstcp_.dec2 = (high_decrease_ - 0.5)/highLowWin; p = exp(hstcp_.p1 + log(cwnd_) * hstcp_.p2); decrease = hstcp_.dec1 + log(cwnd_) * hstcp_.dec2; increase = cwnd_ * cwnd_ * p /(1/decrease - 0.5); answer = increase / cwnd_; return answer; } }
- To use HighSpeed TCP in NS2,
you need to:
- Create a Agent/TCP/Reno
agent
- Set the TCP agent's windowOption_ variable to 8
- Create a Agent/TCP/Reno
agent
- CWND of Ordinary Reno over a 1 Gbps link:
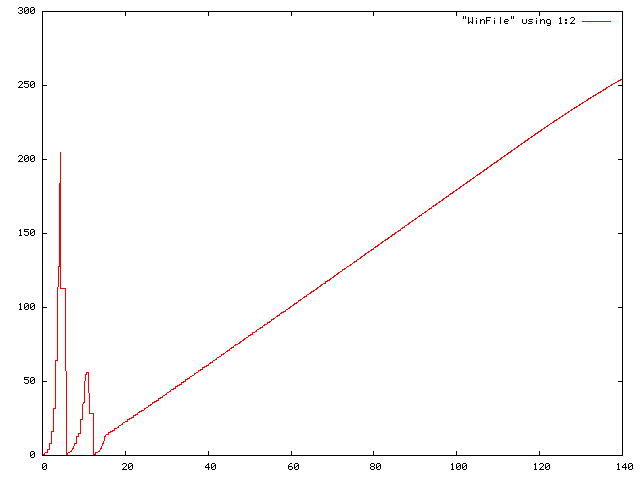
- CWND of HighSpeed TCP over a 1 Gbps link:
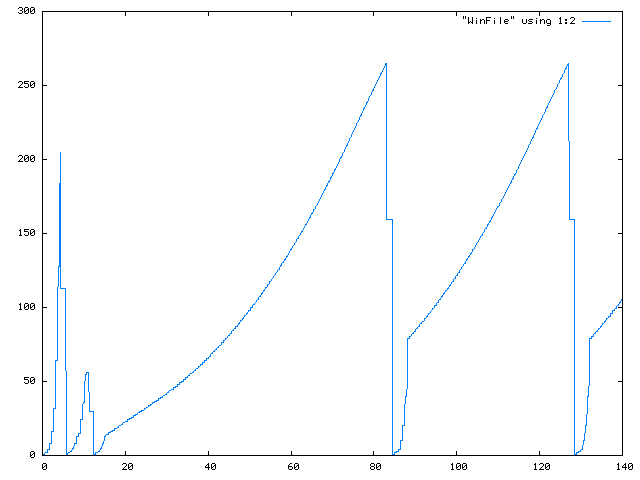
- DEMO:
(Reno vs. HighSpeed TCP)

- Reno NS prog file: click here
- HighSpeed TCP NS prog file: click here