- The
Average Generalized TCP Throughput
is given by the formula
(See: click here):
a Increase: W = W + --- W Decrease: W = W - b * W ------------ 1 / a (2 - b) Avg TCP Throughput = ----- \ / ---------- (# packets/sec) RTT \/ 2bp - We can also conclude that the
Average TCP CWND
is:
------------ / a (2 - b) Avg TCP CWND = \ / ---------- (# packets) \/ 2bp
- Achieving higher throughput in TCP:
- We must use
a larger increase
for each new ACK
I.e.: uses a > 1
- We must use
a larger increase
for each new ACK
- Limiting circumstance:
- We must remember that
other people
are using the
"ordinary (Reno) TCP"
They will not go away when we use a "high speed TCP".
Therefore:
- the new high speed TCP protocol must co-exist with existing network (TCP) protocosl
- We must remember that
other people
are using the
"ordinary (Reno) TCP"
- Herein lies the
difficulty
in the design
(if we can tossed out "Ordinary Reno", any speedier increase
and decrease will work):
- A High speed version of TCP must
be "friendly"
to the "normal" (Reno) TCP
- In other words, when a High speed version of TCP and a
"normal" (Reno) TCP compete for bandwidth over a common
bottle neck link, the "normal" (Reno) TCP
must be starve for bandwidth
We call this property: "TCP-friendly"
- A High speed version of TCP must
be "friendly"
to the "normal" (Reno) TCP
- Considerations:
- TCP Reno cannot
take advantage of
high speed connections
- However, the new High Speed TCP protocol must not overwhelm TCP Reno when operating in a low speed environment
- TCP Reno cannot
take advantage of
high speed connections
- Gist of the design of a TCP Reno-friendly
High Speed TCP protocol:
- The High Speed TCP protocol
uses TCP Reno increase/descrease
when operating
over a low speed connection:
1 Increase: W = W + --- (when a new ACK is received) W Decrease: W = W - 0.5 * W (when 3 dup ACKs are received)
- The High Speed TCP protocol
uses faster increase/descrease
when operating
over a high speed connection:
a Increase: W = W + --- (when a new ACK is received) W Decrease: W = W - b * W (when 3 dup ACKs are received)
$64,000 question:
- How can we tell if the connection is a high speed connection or a low speed connection ?????
Ingenious solution:
- We can tell if a connection is a high speed connection or a low speed connection by the CWND value !!!!
(The "how" is explained below....)
- The High Speed TCP protocol
uses TCP Reno increase/descrease
when operating
over a low speed connection:
- Fact:
- High speed links
(optical fiber) have
very low packet loss
probability
- Loss probability of high speed links are in the order of 10−7
- Low speed links
(copper) have
relatively high packet loss
probability
- Loss probability of high speed links are in the order of 10−3
Average CWND used by classic TCP Reno:
Packet Drop Rate P Congestion Window W ------------------ ------------------- 10^-2 12 10^-3 38 (Low speed links) 10^-4 120 10^-5 379 10^-6 1200 10^-7 3795 (High speed links) 10^-8 12000 10^-9 37948 10^-10 120000 Table 2: TCP Response Function for Standard TCP. The average congestion window W in MSS-sized segments (packets) is given as a function of the packet drop rate P.
Conclussion:
- From the above table, we see that:
- Using a low bandwidth connection, TCP Reno cannot achieve a CWND value > 38 (approximately)
(Assuming that MSS of TCP is approximately 1500 bytes)
- High speed links
(optical fiber) have
very low packet loss
probability
- Summarizes
the "High Speed TCP" algorithm:
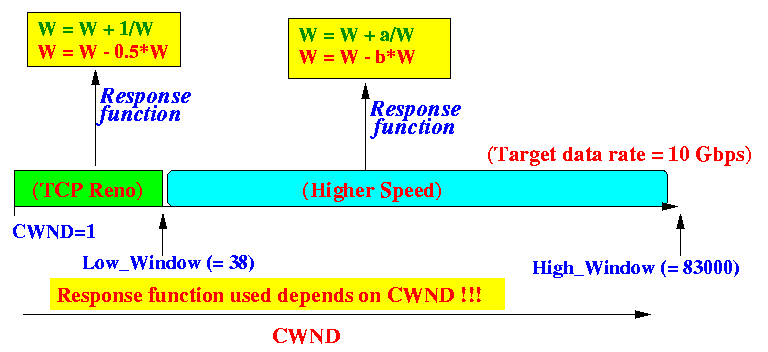
Notes:
- The HighSpeed TCP
will use a
dynamic
increase and decrease functions
that
depended on its current CWND
value.
- To avoid
overwhelming TCP Reno
in low speed networks:
- The increase and decrease method used is the same method used by Reno when CWND ≤ 38
- To fully utilize the
vast amount of bandwidth
in high speed networks:
- The increase and decrease method used is the faster increase/decrease when CWND > 38
- The HighSpeed TCP
will use a
dynamic
increase and decrease functions
that
depended on its current CWND
value.
- Dynamic update rate:
- CWDN update algorithm for
1 ≤ CWND ≤ 38:
1 Increase: CWND = CWND + ------ CWND Decrease: CWND = CWND - 0.5 * CWND
- CWDN update algorithm for
CWND > 38
is dynamically changing
with the value of CWND:
a(CWND) Increase: CWND = CWND + ------ CWND Decrease: CWND = CWND - b(CWND) * CWND
Example: (not scientifically correct, just to illustrate the concept of "dynamic update rate")
- CWND ≤ 38
1 Increase: CWND = CWND + ------ CWND Decrease: CWND = CWND - 0.5 * CWND
- CWND = 40
2 Increase: CWND = CWND + ------ CWND Decrease: CWND = CWND - 0.45 * CWND
- CWND = 50
3 Increase: CWND = CWND + ------ CWND Decrease: CWND = CWND - 0.42 * CWND
- Dynamic update rate:
- The factors
a and
b
changes
with the
current congestion window size CWND
I.e.:
- a = a(W)
- b = b(W)
(The paper uses W to denote CWND)
- The factors
a and
b
changes
with the
current congestion window size CWND
- CWDN update algorithm for
1 ≤ CWND ≤ 38:
- The authors assumed the following
ball park (representative) values:
- Payload in TCP segment (packet size) = 1500 bytes
- RTT = 0.1 sec
- Throughput of TCP when using CWND = W:
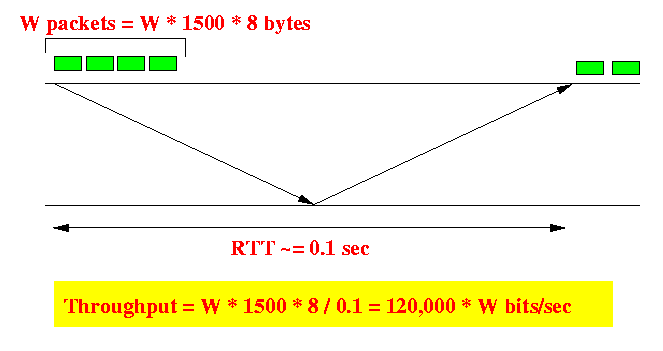
- CWND that yield 10 Gbps throughput:
120,000 × CWND = 1,000,000,000 ==> CWND = 1,000,000,000 / 120,000 = 83,333 ==> CWND ~= 83,000
- Conclusion:
- The High Speed TCP
increase/decrease algorithm
must allow CWND to
reach
CWND ~= 83,000
(using a high speed connection with packet drop probability of p = 10−7)
- The High Speed TCP
increase/decrease algorithm
must allow CWND to
reach
CWND ~= 83,000
- Recall
the general TCP throughput and CWND formulas:
------------ / a (2 - b) 1 Avg TCP Throughput = \ / ---------- × ------- \/ 2bp RTT ------------ / a (2 - b) Avg TCP CWND = \ / ---------- \/ 2bp
- CWND increase/decrease method
that can reach
CWND = 83,000
when
p = 10−7:
------------- / a (2 - b) 83000 = \ / ---------- \/ 2b * 10−7
Or: ----------------- / a (2 - b) 83000 = \ / ---------- * 107 \/ 2b
- Summary:
- If the
packet loss probability is
equal to 10−7
and the TCP CWND update algorithm
uses:
a Increase: CWND = CWND + ------ CWND Decrease: CWND = CWND - b * CWND
such that a and b satisfy the relationship:
----------------- / a (2 - b) 83000 = \ / ---------- * 107 \/ 2bthen:
- The TCP CWND will
reach an average value of
CWND = 83,000
- (Assuming the packet size = 1500 bytes, the average TCP throughput will be 10 Gbps)
- The TCP CWND will
reach an average value of
CWND = 83,000
- If the
packet loss probability is
equal to 10−7
and the TCP CWND update algorithm
uses:
- Note:
- There are infinitely many solutions for a and b
- Possible solution 1:
a = 72 and
b = 0.1
Verify: --------------------- / 72 (2 - 0.1) \ / ------------- * 107 \/ 2*0.1 ------------------ / 72 * 1.9 = \ / ---------- * 107 \/ 0.2 -------- / = \ / 684 * 107 \/ = 82704.29 (approximately 83000)
- Possible solution 2:
a = 459
and
b = 0.5:
Verify: --------------------- / 459 (2 - 0.5) \ / ------------- * 107 \/ 2*0.5 ------------------ / 459 * 1.5 = \ / ---------- * 107 \/ 1.0 -------- / = \ / 688.5 * 107 \/ = 82975.90 (also approximately 83000)
- Consider the choice between:
- (a = 72 and b = 0.1)
- (a = 459 and b = 0.5)
Which CWND update method is better ?
- (a = 72 and
b = 0.1):
- If there are no packet losses
in a round of transmission
(RTT = 0.1 sec),
the CWND of
the TCP connection will
increase 72 packets
- If there are packet losses resulting in 3 duplicate ACKs in a round of transmission, the CWND of TCP connection will decrease by 0.1 × CWND (a 10% decrease)
- If there are no packet losses
in a round of transmission
(RTT = 0.1 sec),
the CWND of
the TCP connection will
increase 72 packets
- (a = 459 and
b = 0.5):
- If there are no packet losses
in a round of transmission
(RTT = 0.1 sec),
the CWND of
the TCP connection will
increase 459 packets
- If there are packet losses resulting in 3 duplicate ACKs in a round of transmission, the CWND of TCP connection will decrease by 0.5 × CWND (a 50% decrease)
- If there are no packet losses
in a round of transmission
(RTT = 0.1 sec),
the CWND of
the TCP connection will
increase 459 packets
- Finding:
- TCP using a = 72 and b = 0.1 results in a much gradual increase in CWND
- Bottomline:
- The designers of HighSpeed TCP
has decided on:
- a = 72 and b = 0.1
as the most suitable values
- The designers of HighSpeed TCP
has decided on:
- Summary of the findings:
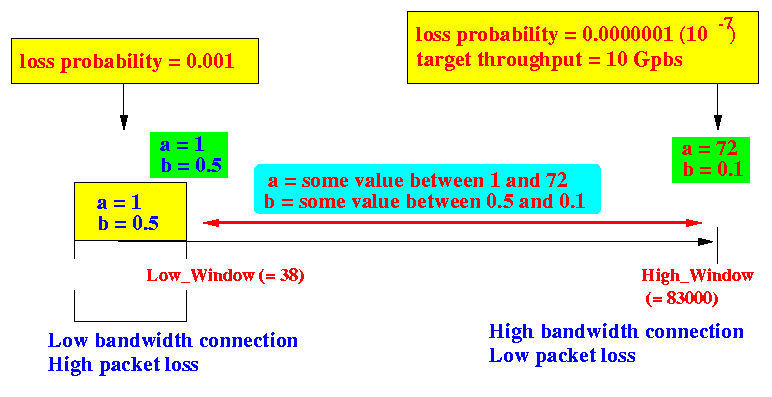
Notes:
- TCP Reno operates well in
low bandwidth connections
The increase/decrease parameters of TCP Reno are:
- a = 1
- b = 0.5
- We have found that to achieve 10 Gbps
throughput over a
high bandwidth connection,
High Speed TCP will use as
increase/decrease
parameters:
- a = 72
- b = 0.1
- TCP Reno operates well in
low bandwidth connections
- High Speed TCP uses
dynamic increase/decrease parameters
that depends on the
network reliability (or CWND):
- a = a(CWND)
- b = b(CWND)
$64,000 Question:
- What functions do we use for a(CWND) and b(CWND) ???
Initial answer:
- When High Speed TCP
detects that it is
operating in
a low bandwidth connection
(i.e., CWND ≤ 38),
High Speed TCP
will use:
- a = 1
- b = 0.5
(This will ensure TCP (Reno) friendiness)
- When High Speed TCP
detects that it is
operating in
a high bandwidth connection
(i.e., CWND = 83,000),
High Speed TCP
will use:
- a = 72
- b = 0.1
- Between these
two extreme values:
- The value of a will gradually change from 1 to 72 depending on CWND
- The value of b will gradually change from 0.5 to 0.1 depending on CWND
- I.e.:

- Plot of
CWND vs.
Packet drop probability
(i.e., a function W(p)):

So far:
- We only have
2 operational points:
- For p = 10−7 (low loss/high speed connection), TCP should use CWND = 83,000
- For p = 10−3 (high loss/low speed connection), TCP should use CWND = 38
- Between these
2 extreme (end) points,
we need to find a
smooth function
This can be done through interpolation
Question:
- What is the "best" interpolation function W(p) ???
- We only have
2 operational points:
- Possible interpolation function W(p):
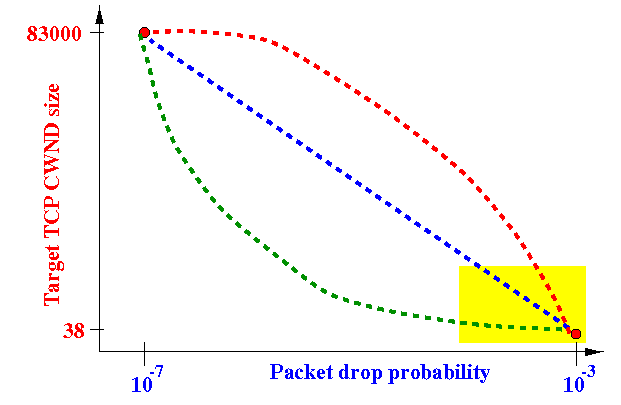
Observation on the interpolation functions:
- The red interpolation function
will cause
CWND to
increase rapidly
when
p drop slightly
below 10−3
- Such a rapid increase in CWND is not appropriate for the level of network reliability
- The green interpolation function will cause CWND to increase rapidly only when p is very small (~ 10−7)
- The red interpolation function
will cause
CWND to
increase rapidly
when
p drop slightly
below 10−3
- Conclusion:
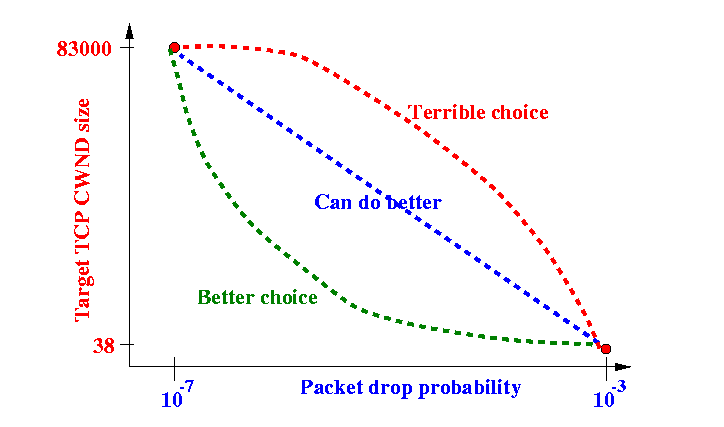
Note:
- The green plot looks like W(p) = 1/p....
- Consider an interpolation function of the form:
u W(p) = ----- pv
- W(p) must satisfy:
W( 10−7 ) = 83,000 ........ (1) W( 10−3 ) = 38 ........ (2)We can find u and v as follows:
u ------ = 83,000 ........ (1a) (10−7)v u ------ = 38 ........ (2a) (10−3)v
Or: u = 83,000 × (10−7)v ........ (1b) u = 38 × (10−3)v ........ (2b)
==> 83,000 × (10−7)v = 38 × (10−3)v <==> log(83,000) + log(10−7)v = log(38) + log(10−3)v <==> 4.919 - 7v = 1.580 - 3v <==> 4v = 3.339
Therefore:v = 0.835 ...... (3)
u = 38 × (0.001)0.835 = 0.12 ...... (4)
- Proposed
function W(p): :
0.12 W(p) = --------- . . . . . . . . . . . . . . (5) 0.835 p - Plot of W(p):
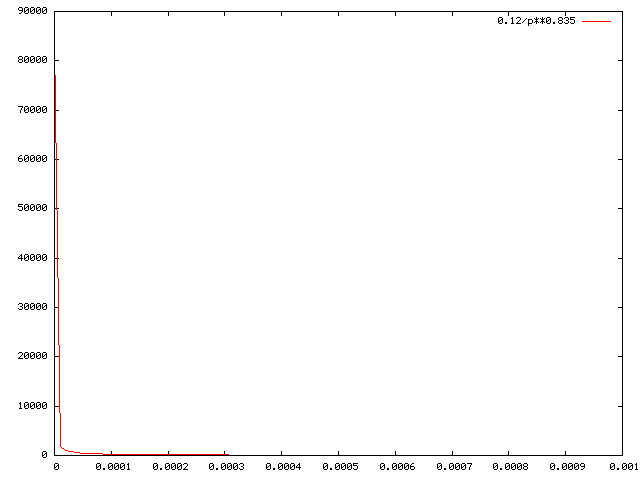
(The scale is too large :-))
- In the design of the
HS-TCP protocol,
we will need to:
- Find the drop probability p for a given (average) CWND quickly...
- So us will compute the
inverse function
p(W) here:
0.12 W = --------- 0.835 p 0.12 <==> p0.835 = ------ (1/(0.835) = 1.1976) W 0.121.1976 <==> p = ------------ W1.1976
0.0789 p(W) = --------- . . . . . . . . . . . . . (6) W1.2
- Recall that
the High Speed (HS) TCP protocol
uses dynamic a and b
that depends on the
CWND value w:
- Note: w = current congestion window (CWND)
a(w) Increase: w <- w + ------ w Decrease: w <- w - b(w) * w
- Recall also
the general TCP throughput and CWND formulas:
------------ / a (2 - b) 1 Avg TCP Throughput = \ / ---------- × ------- ........ (7) \/ 2bp RTT ------------ / a (2 - b) Avg TCP CWND = \ / ---------- (# packets) ........ (8) \/ 2bp
- We write Equation (8)
in a different form:
-------------- / a (2 - b) w = \ / ------------- (# packets) \/ 2 b p 2 a (2 - b) <==> w = ----------- 2 b p <==> a * (2 - b) = w2 * 2 * b * p 2 w2 b p <==> a = ---------- 2 - b
Or:2 w2 b(w) p(w) a(w) = ---------------- . . . . . . . . . (9) 2 - b(w)
- Recall the relationship
between CWND w and
the packet loss probability p:
(See: click here )
0.0789 p(W) = --------- . . . . . . . . . . . . . (6) W1.2
Notice that there are two undetermined variables (degrees of freedom) in Equation (9):
2 w2 b(w) p(w) a(w) = ---------------- . . . . . . . . . (9) 2 - b(w)Namely:
- a(w)
- b(w)
- w is
not a
degree of freedom because
it is the parameter
on which the other values depends)
- p(w) is not a degree of freedom because it is already determined by the throughput formula of TCP Reno)
- In other words:
-
We can choose
a value for
one of the parameters
(a(w) or b(w)), and
then compute the value
of the other one
in Equation (9)
- From the form of
Equation (9):
2 w2 b(w) p(w) a(w) = ---------------- . . . . . . . . . (9) 2 - b(w)It is obvious that we should:
- Choose
the value for
b(w)
- use Equation (3) to compute the value of a(w)....
- Choose
the value for
b(w)
- Note that
we cannot choose arbitrary values
for b(w)
because:
- When w = 38 (low speed connection), HS-TCP must used a factor of b(w) = 0.5 for the decrement operation
- When w = 83,000 (high speed bandwidth connection), HS-TCP must used a factor of b(w) = 0.1 for the decrement operation
Graphically:
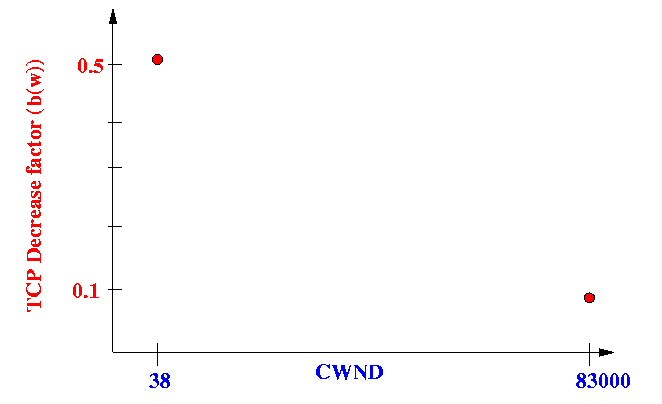
- To choose an
appropriate value for
b(w) ,
we can use
interpolation....
Consider the choices:
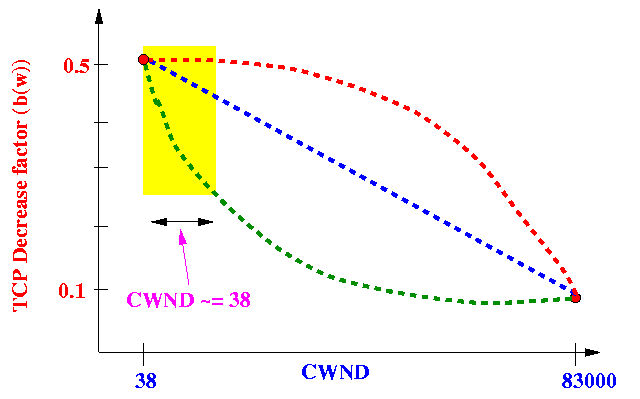
Note:
- Using the red interpolation line,
TCP will
decrement
CWND
more rapidly
(CWND decreases by approximately 0.5 or 50%)
- Using the green interpolation line,
TCP will
decrement
CWND
more gradually
(CWND decreases by approximately 0.3-0.4 or 30%-40%)
- Using the red interpolation line,
TCP will
decrement
CWND
more rapidly
- The authors' choice for
b(w) :
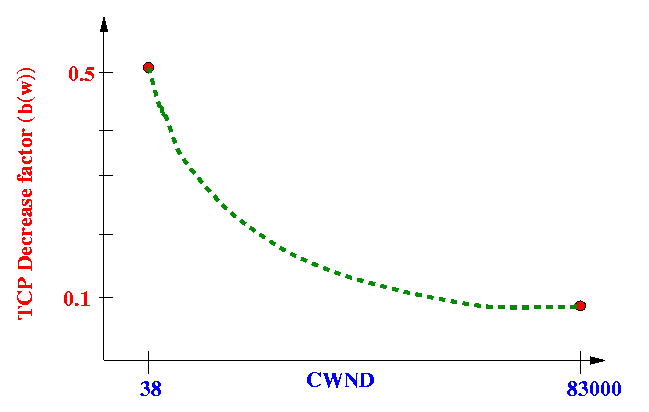
- The designers of the
HighSpeed TCP protocol
uses the following
Interpolation curve for
b(w) :
log(w) - log(38) b(w) = (0.1 - 0.5) * ---------------------- + 0.5 . . . . . (10) log(83000) - log(38)
The Interpolation curve for b(w) looks like this:
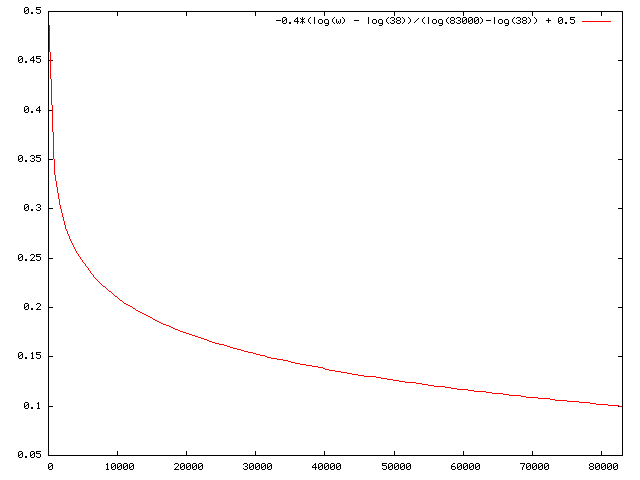
- Personally, I disgree with the
choice:
- The factor
b is used
to decrease TCP traffic
- Fact:
- You want to reduce traffic
immediately
when the network is congested
- I.e.: you want to keep b as large as possible for as long as possible
- You want to reduce traffic
immediately
when the network is congested
- Personally, I think the
red interpolation curve
is better....
(Just a gut feeling....)
(I will continue with the paper....)
- The factor
b is used
to decrease TCP traffic
- CWND update method in
HS-TCP:
a(w) New ACK: w <- w + ------ w Triple Dup ACK: w <- w - b(w) * wa(w) and b(w) depends on the current congestion window CWND = w.
- Assume that the
current congestion window CWND is
equal to:
- CWND = w
- The factor
b(w) is
interpolated using the
formula:
log(w) - log(38) b(w) = (0.1 - 0.5) * ---------------------- + 0.5 .......(10) log(83000) - log(38)
- After computing b(w),
the term a(w) is
computed using
Equation (9):
(See: click here )
2 w2 b(w) p(w) a(w) = ---------------- .......... (9) 2 - b(w)The value p(w) is computed from w using Equation (6):
0.0789 p(w) = --------- ........ (6) w1.2
- The implemation code
of the HighSPeed TCP
can be found
in NS2 in the file
NS-DIR/tcp/tcp.cc:
click here
- Look for the method
"double TcpAgent::decrease_param()"
to find b(w)
- Look for the method
"double TcpAgent::increase_param()"
to find a(w)
- Here is a "cleaned up"
code segment
of the HighSpeed TCP algorithm
in NS2:
# These values are set in TCL Agent/TCP set low_window_ 38 ; # default changed on 2002/8/12. Agent/TCP set high_window_ 83000 Agent/TCP set high_p_ 0.0000001 # 10^-7 Agent/TCP set high_decrease_ 0.1 Agent/TCP set max_ssthresh_ 0
double TcpAgent::decrease_param() { double decrease; // ============================================ // These values has been computed elsewhere: // ============================================ // hstcp_.dec1 = 0.5 - log(low_window_) * (high_decrease_ - 0.5)/highLowWin; // hstcp_.dec2 = (high_decrease_ - 0.5)/highLowWin; decrease = hstcp_.dec1 + hstcp_.dec2 * log(cwnd_); // They have re-worked Equation (10) into // the form: // b = constant1 + constant2 * log(w) return decrease; }
double TcpAgent::increase_param() { double increase, decrease, p, answer; // p ranges from 1.5/W^2 at congestion window low_window_, to // high_p_ at congestion window high_window_, on a log-log scale. // The decrease factor ranges from 0.5 to high_decrease // as the window ranges from low_window to high_window, // as the log of the window. // For an efficient implementation, this would just be looked up // in a table, with the increase and decrease being a function of the // congestion window. if (cwnd_ <= low_window_) { answer = 1 / cwnd_; // Standard Reno: CWND = CWND + 1/CWND return answer; } else { // ============================================ // These values has been computed elsewhere: // ============================================ // hstcp_.p1 = log(hstcp_.low_p) // - log(low_window_) * highLowP/highLowWin; // hstcp_.p2 = highLowP/highLowWin; // hstcp_.dec1 = 0.5 - log(low_window_) // * (high_decrease_ - 0.5)/highLowWin; // hstcp_.dec2 = (high_decrease_ - 0.5)/highLowWin; p = exp(hstcp_.p1 + log(cwnd_) * hstcp_.p2); decrease = hstcp_.dec1 + log(cwnd_) * hstcp_.dec2; // decrease = b(w) increase = cwnd_ * cwnd_ * p /(1/decrease - 0.5); // (w * w * p)/(1/b - 0.5) // = (w2 b p) / (1 - 0.5*b) // = (2 w2 b p ) / (2 - b) answer = increase / cwnd_; return answer; } }
- How to use
HighSpeed TCP in NS2:
- Create a Agent/TCP/Reno
agent
- Set the TCP agent's windowOption_ variable to 8
- Create a Agent/TCP/Reno
agent
- Example CWND change - Reno vs. HS-TCP:
- CWND of TCP Reno over a
1 Gbps link:
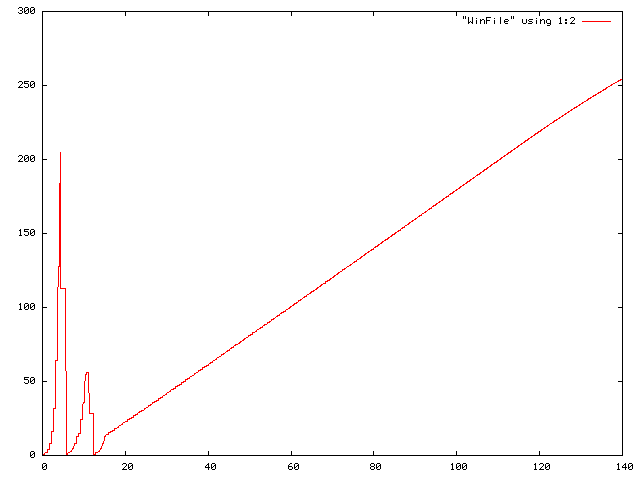
- CWND of HS-TCP over a
1 Gbps link:
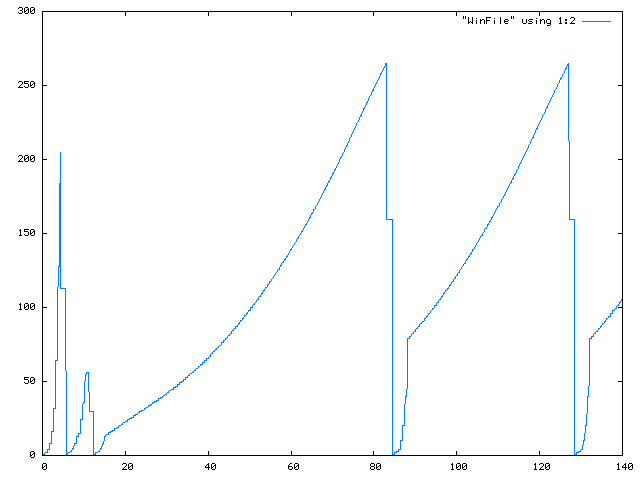
- CWND of TCP Reno over a
1 Gbps link:
- DEMO:
(Reno vs. HighSpeed TCP)

- Reno NS prog file: click here
- HighSpeed TCP NS prog file: click here